
আমরা আমাদের আর্টিকেলে দশম শ্রেণীর ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় ‘চলতড়িৎ’ এর কিছু গাণিতিক উদাহরণ নিয়ে আলোচনা করবো। এই প্রশ্নগুলো দশম শ্রেণীর ভৌতবিজ্ঞান পরীক্ষার জন্য ও প্রতিযোগিতামূলক পরীক্ষার জন্য অনেক গুরুত্বপূর্ণ।
তড়িদাধান ও কুলম্বের সূত্র
বায়ুতে দুটি বিন্দু-আধান 25 esu ও 12 esu পরস্পর 5 cm ব্যবধানে। আধান দুটির মধ্যে ক্রিয়াশীল বল নির্ণয় করো।
প্রথম আধান \( \left(q_1\right)=25\;esu \), দ্বিতীয় আধান \( \left(q_2\right)=12\;esu \), আধান দুটির ব্যবধান \( \left(r\right)=5\;cm \)।
আধান দুটির মধ্যে পারস্পরিক বল, \( F=\frac{q_1q_2}{r^2} \)
বা, \( F=\frac{25\times12}{5^2} \)
বা, \( F=12\;dyn \)
∴ আধান দুটির মধ্যে ক্রিয়াশীল বল \( \left(F\right)=12\;dyn \)।
বায়ুতে দুটি বিন্দু-আধান 2 m ব্যবধানে আছে। একটি আধানের মান অপরটির দ্বিগুণ। আধান দুটির পারস্পরিক বিকর্ষণ বল \( 7.2\times10^{10}\;N \) হলে, প্রতিটি আধানের মান কত?
মনে করি, প্রথম আধান, \( q_1=q\;C \) ও দ্বিতীয় আধান, \( q_2=2q\;C \), আধান দুটির ব্যবধান, \( r=2\;m \)।
পারস্পরিক বিকর্ষণ বল \( \left(F\right)=7.2\times10^{10}\;N \)
∴ \( F=9\times10^9\cdot\frac{q_1q_2}{r^2} \) সমীকরণ থেকে পাই,
বা, \( 2q^2\times9\times10^9=4\times7.2\times10^{10} \)
বা, \( q^2=\frac{4\times7.2\times10^{10}}{2\times9\times10^9} \)
বা, \( q^2=16 \)
বা, \( q=\pm4 \)
∴ \( q_1=4\;C \) হলে, \( q_2=2\times4\;C=8\;C \)
আবার, \( q_1=-4\;C \) হলে, \( q_2=-2\times4\;C=-8\;C \)
দুটি বিন্দু-আধানকে \( r \) ব্যবধানে রাখলে পারস্পরিক তাড়িতিক বল হয় \( F \)। ব্যবধান কত হলে বলের মান \( \frac F2 \) হবে?
আধান দুটি \( q_1 \) ও \( q_2 \) হলে \( F=k\cdot\frac{q_1q_2}{r^2} \) ___(1) যেখানে k হল ধ্রুবক।
মনে করি, আধান দুটির মধ্যবর্তী ব্যবধান \( x \) হলে পারস্পরিক বলের মান হবে, \( F_1=\frac F2 \)।
∴ \( F_1=k\cdot\frac{q_1q_2}{x^2} \) ___(2)
(1) ÷ (2) নং করে পাই,
বা, \( 2=\frac{x^2}{r^2} \)
বা, \( x^2=2r^2 \)
বা, \( x=\sqrt2r \)
∴ ব্যবধান \( x=\sqrt2r \) হলে বলের মান \( \frac F2 \) হবে।
\( A \) বস্তুকে \( B \) বস্তু দ্বারা ঘর্ষণ করার ফলে \( A \) বস্তুতে আধান হল \( 4.8\mu C \)। ঘর্ষণ প্রক্রিয়ায় ক-টি ইলেকট্রনের আদান-প্রদান হয়েছে?
একটি ইলেকট্রনের আধানের মান \(\left(e\right)=1.6\times10^{-19}\;C \)।
A বস্তুর আধান \( \left(q\right)=4.8\mu C=4.8\times10^{-6}\;C \)।
এই প্রক্রিয়ায় \(x\)টি ইলেকট্রনের স্থানান্তরণ হলে,
\( x=\frac qe \\\)বা, \( x=\frac{4.8\times10^{-6}}{1.6\times10^{-19}}=3\times10^{13} \)
∴ ঘর্ষণ প্রক্রিয়ায় \( A \) বস্তু থেকে \( B \) বস্তুতে \( 3\times10^{13} \)টি ইলেকট্রন স্থানান্তরিত হয়েছে।
\( A \) বস্তুকে \( B \) বস্তুর দ্বারা ঘর্ষণ করার ফলে \( A \) বস্তুর আধান হল \( 6.4\times10^{-8}\;C \)। \( A \) বস্তুর ভরের কীরূপ পরিবর্তন হবে?
একটি ইলেকট্রনের আধানের মান \( \left(e\right)=1.6\times10^{-19}\;C \)।
\( A \) বস্তুর আধান \( \left(q\right)=6.4\times10^{-8}\;C \)।
ঘর্ষণ প্রক্রিয়ার ফলে \(x\)টি ইলেকট্রনের স্থানান্তরণ হলে,
\( x=\frac qe \\\)বা, \( x=\frac{6.4\times10^{-8}}{1.6\times10^{-19}} \)
∴ \( x=4\times10^{11} \)
∴ ঘর্ষণ প্রক্রিয়ায় \( A \) বস্তু থেকে \( B \) বস্তুতে \( 4\times10^{11} \)টি ইলেকট্রন স্থানান্তরিত হয়েছে।
আবার, একটি ইলেকট্রনের ভর \( \left(m\right)=9.1\times10^{-31}\;kg \)
∴ বস্তুর ভর-হ্রাসের পরিমাণ
\( =mx\\\)\( =9.1\times10^{-31}\times4\times10^{11} \\\)\( =3.64\times10^{-19}\;kg \\\)∴ \( A \) বস্তুর ভরের \(3.64\times10^{-19}\;kg \) পরিবর্তন হবে।
\( 2\times10^{-8}\;C \) তড়িদাধানসম্পন্ন দুটি কণা \( 1\;m \) দৈর্ঘ্যের সিল্কের সুতো দিয়ে বেঁধে একটি অন্তরিত, মসৃণ অনুভূমিক টেবিলের ওপর রাখা হল। সুতোটিতে কতখানি টান পড়বে?
প্রত্যেকটি কণার আধান \( \left(q\right)=2\times10^{-8}\;C \), সুতোর দৈর্ঘ্য \( \left(r\right)=1\;m \)।
∴ পারস্পরিক বিকর্ষণ বল,
\( F=9\times10^9\cdot\frac{q^2}{r^2} \) [SI এককে, \( k=9\times10^9N\cdot m^2\cdot C^{-2}\rbrack \)
বা, \( F=9\times10^9\times\frac{\left(2\times10^{-8}\right)^2}{1^2} \)
বা, \( F=3.6\times10^{-6}\;N \)
বা, \( F=3.6\times10^{-6}\times10^5\;dyn \)
বা, \( F=0.36\;dyn \)
∴ সুতোটিতে \(0.36\;dyn \) টান পড়বে।
তড়িৎপ্রবাহ, বিভবপ্রভেদ ও ওহমের সূত্র
কোনো পরিবাহীর কোনো প্রস্থচ্ছেদের মধ্য দিয়ে 2 min সময়ে 45 C আধান প্রবাহিত হলে তড়িৎপ্রবাহ কত হবে?
প্রবাহিত আধান \( q=45\;C \),
সময় \( t=2\;min=2\times60\;s=120\;s \)
∴ তড়িৎপ্রবাহ,
\( I=\frac qt \\\)বা, \( I=\frac{45\;C}{120\;s} \)
বা, \( I=0.375\;A \)
∴ তড়িৎপ্রবাহ \(\left(I\right)=0.375\;A \) হবে।
কোনো পরিবাহীর মধ্য দিয়ে 2 A প্রবাহমাত্রা চলছে। 5 s সময়ে কত আধান প্রবাহিত হয়? পরিবাহীতে আধানের বাহক মুক্ত ইলেকট্রন হলে পরিবাহীর কোনো প্রস্থচ্ছেদের মধ্য দিয়ে কতগুলি ইলেকট্রন প্রবাহিত হবে?
তড়িৎপ্রবাহ, \( \left(I\right)=2\;A \), সময় \( \left(t\right)=5\;s \)।
\( q \) পরিমাণ আধান প্রবাহিত হলে \( I=\frac qt \)
বা, \( q=It=2\times5 \)
বা, \( q=10\;C \)
একটি ইলেকট্রনের আধানের মান \( \left(e\right)=1.6\times10^{-19}\;C \)
∴ পরিবাহীর কোনো প্রস্থচ্ছেদের মধ্য দিয়ে প্রবাহিত ইলেকট্রন সংখ্যা
\( =\frac qe \)টি
\( =\frac{10}{1.6\times10^{-19}} \)টি
\( =6.25\times10^{19} \)টি
∴ পরিবাহীর কোনো প্রস্থচ্ছেদের মধ্য দিয়ে প্রবাহিত ইলেকট্রন সংখ্যা \( 6.25\times10^{19} \)টি
একটি পরিবাহীর দু-প্রান্তের বিভবপ্রভেদ \( 5\;V \) ও রোধ \( \;10\;\Omega \)। প্রবাহমাত্রা কত?
পরিবাহীর রোধ \( \left(R\right)=10\;\Omega \), বিভবপ্রভেদ \( \left(V\right)=5\;V \)।
মনে করি, প্রবাহমাত্রা \( =I \)
ওহমের সূত্র থেকে পাই,
\( V=IR \\\)বা, \( I=\frac VR \)
বা, \( I=\frac{5\;V}{10\;\Omega} \)
বা, \( I=0.5\;A \)
∴ প্রবাহমাত্রা \( \left(I\right)=0.5\;A \)।
কোনো পরিবাহীর দু-প্রান্তে 10 V বিভবপার্থক্য প্রয়োগ করলে 0.1 A তড়িৎপ্রবাহ হয়। পরিবাহীর রোধ কত?
পরিবাহীর দু-প্রান্তের বিভবপ্রভেদ \( \left(V\right)=10\;V \), প্রবাহমাত্রা \( \left(I\right)=0.1\;A \)
পরিবাহীর রোধ \( =R \) হলে, ওহমের সূত্রানুযায়ী,
\( V=IR \\\)বা, \( R=\frac VI \)
বা, \( R=\frac{10\;V}{0.1\;A} \)
বা, \( R=100\;\Omega \)
∴ পরিবাহীর রোধ \( \left(R\right)=100\;\Omega \)।
দুটি পরিবাহীর প্রথমটির রোধ দ্বিতীয়টির তিনগুণ, প্রথমটির মধ্য দিয়ে তড়িৎপ্রবাহ দ্বিতীয়টির দ্বিগুণ। পরিবাহী দুটির বিভবপ্রভেদের অনুপাত কত?
মনে করি, দ্বিতীয় পরিবাহীর রোধ \( =R \) ও তড়িৎপ্রবাহ \( =I \)
∴ প্রথম পরিবাহীর রোধ \( =3R \) ও প্রবাহমাত্রা \( =2I \)
প্রথম পরিবাহীর দু-প্রান্তের বিভবপ্রভেদ,
\( V_1=3R\times2I=6RI \)ও দ্বিতীয় পরিবাহীর দু-প্রান্তের বিভবপ্রভেদ,
\( V_2=RI \\\)∴ \( \frac{V_1}{V_2}=\frac{6RI}{RI}=6 \)
∴ \( V_1:V_2=6:1 \)
∴ পরিবাহী দুটির বিভবপ্রভেদের অনুপাত \( V_1:V_2=6:1 \)
1.5 V তড়িৎচালক বলের একটি তড়িৎকোশকে কোনো বর্তনীতে যুক্ত করলে 1 A প্রবাহমাত্রা চলে এবং বহির্বর্তনীর প্রান্তীয় বিভবপ্রভেদ হয় 1 V। কোশের অভ্যন্তরীণ রোধ কত?
তড়িৎকোশের তড়িৎচালক বল \( \left(E\right)=1.5\;V \), বহির্বর্তনীর প্রান্তীয় বিভবপ্রভেদ \( \left(V\right)=1\;V \), বর্তনীতে প্রবাহমাত্রা \( \left(I\right)=1\;A \)
মনে করি, তড়িৎকোশের অভ্যন্তরীণ রোধ \( =r \)
∴ \( rI=E-V \)
বা, \( r\times1=1.5-1 \)
বা, \( r=0.5\;\Omega \)
∴ কোশের অভ্যন্তরীণ রোধ \( \left(r\right)=0.5\;\Omega \)।
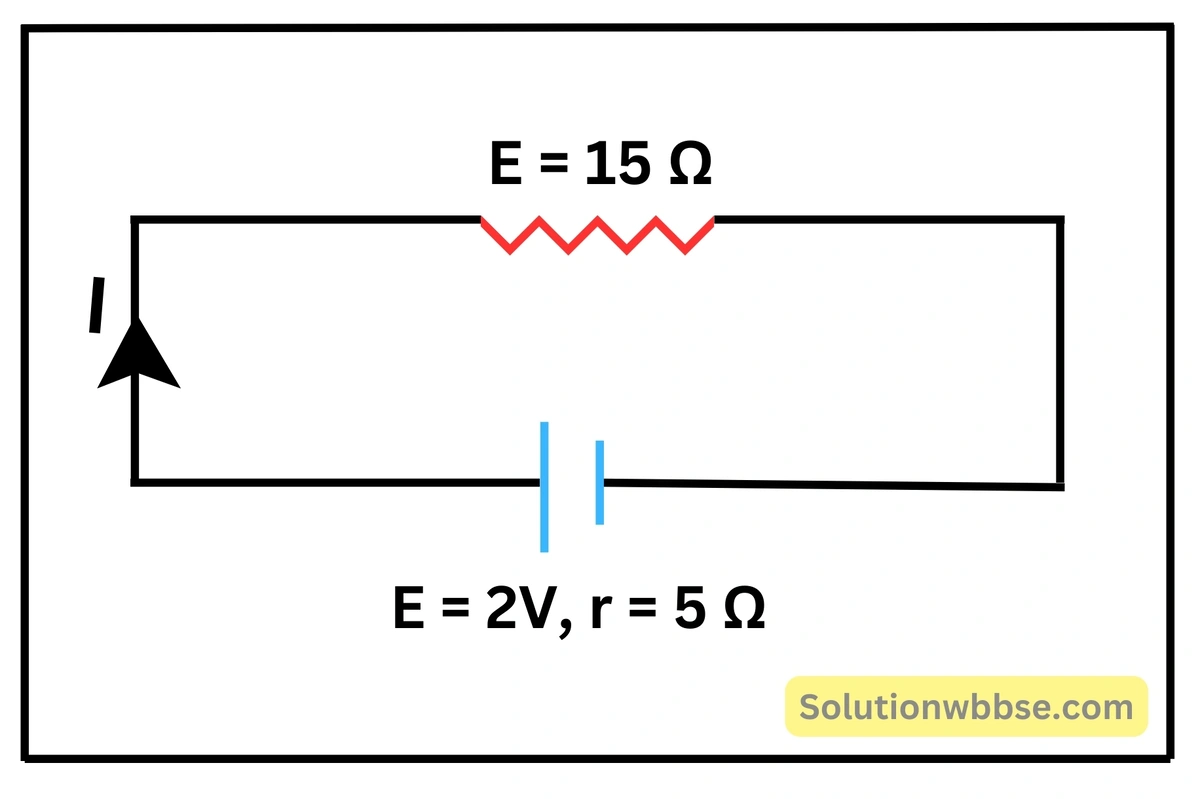
\( 5\;\Omega \) অভ্যন্তরীণ রোধ ও \( 2\;V \) তড়িৎচালক বলবিশিষ্ট একটি তড়িৎকোশকে \( 15\;\Omega \) রোধের সঙ্গে যুক্ত করা হল। কোশের প্রান্তদ্বয়ের মধ্যে বিভবপ্রভেদ কত হবে?
তড়িৎকোশের তড়িৎচালক বল \( \left(E\right)=2\;V \), অভ্যন্তরীণ রোধ \( \left(r\right)=5\;\Omega \) এবং বহির্বর্তনীর রোধ \( \left(R\right)=15\;\Omega \)
মনে করি, বর্তনীতে তড়িৎপ্রবাহ \( =I \)
∴ \( I=\frac E{R+r} \)
বা, \( I=\frac2{15+5} \)
বা, \( I=0.1\;A \)
∴ কোশের প্রান্তদ্বয়ের মধ্যে বিভবপ্রভেদ, \( V=IR=0.1\times15=1.5\;V \)
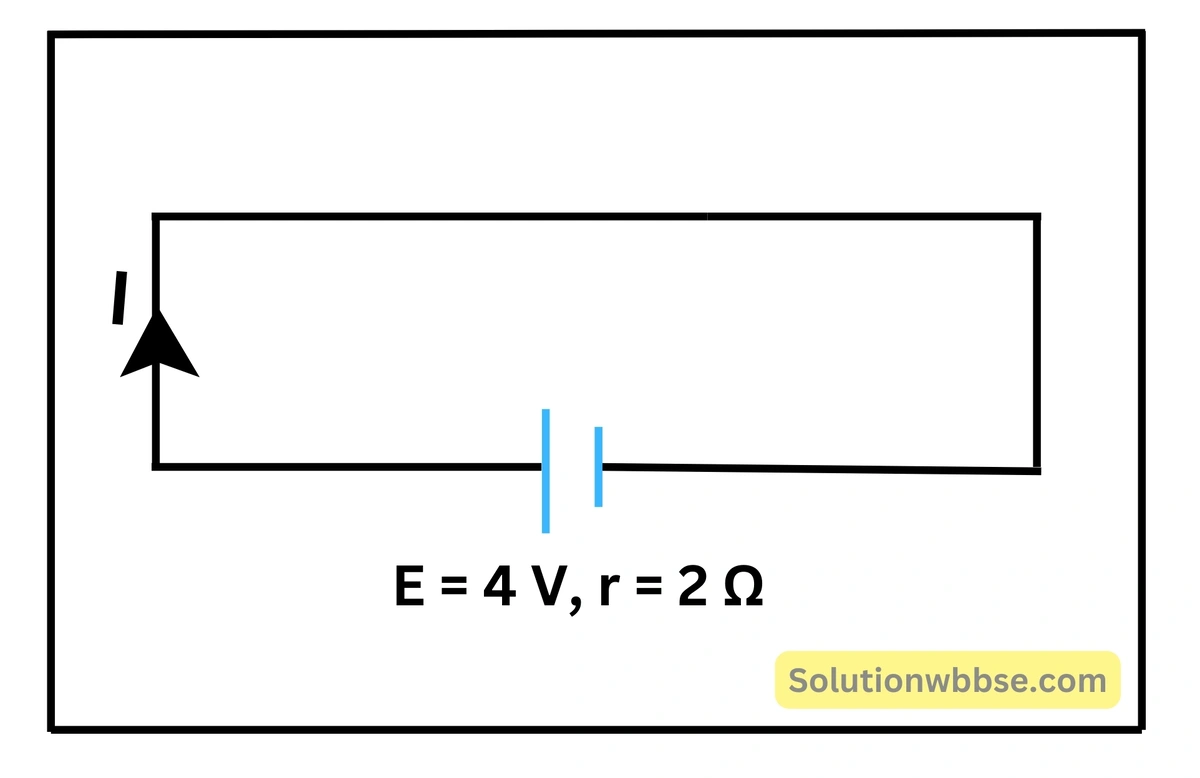
একটি তড়িৎকোশের তড়িৎচালক বল \( 4\;V \) ও অভ্যন্তরীণ রোধ \( 2\;\Omega \)। কোশটির সর্বোচ্চ প্রবাহমাত্রা কত?
তড়িৎকোশের তড়িৎচালক বল \( \left(E\right)=4\;V \) ও অভ্যন্তরীণ রোধ \( \left(r\right)=2\;\Omega \)।
কোশটির মেরু দুটির সঙ্গে নগণ্য রোধের একটি পরিবাহী তার দ্বারা যুক্ত করলে, বহির্বর্তনীর রোধ \( R=0 \) ধরা যেতে পারে। এক্ষেত্রে বর্তনীতে প্রবাহমাত্রা সর্বোচ্চ হবে।
∴ সর্বোচ্চ প্রবাহমাত্রা, \( I_{max}=\frac Er \)
বা, \( I_{max}=\frac{4\;V}{2\Omega} \)
∴ \( I_{max}=2\;A \)
একটি তড়িৎকোশের তড়িৎচালক বল \( 5\;V \)। মুক্ত বর্তনীতে কোশের অভ্যন্তরে \( 1\;C \) আধানকে ঋণাত্মক তড়িদ্দ্বার থেকে ধনাত্মক তড়িদ্দ্বারে নিয়ে যেতে বাহ্যিক সংস্থাকে কত কার্য করতে হবে?
তড়িৎকোশের তড়িৎচালক বল \( \left(E\right)=5\;V \), মুক্ত বর্তনীতে তড়িৎকোশের অভ্যন্তরে, \( q=1\;C \)।
আধানকে ঋণাত্মক তড়িদ্দ্বার থেকে ধনাত্মক তড়িদ্দ্বারে নিয়ে যেতে বাহ্যিক সংস্থা দ্বারা কৃত কার্য
\( W=qE\\ \)বা, \( W=1\;C\times5\;V \)
বা, \( W=5\;J \)
∴ মুক্ত বর্তনীতে কোশের অভ্যন্তরে \( 1\;C \) আধানকে ঋণাত্মক তড়িদ্দ্বার থেকে ধনাত্মক তড়িদ্দ্বারে নিয়ে যেতে বাহ্যিক সংস্থাকে \( 5\;J \) কার্য করতে হবে।
একটি তড়িৎকোশের তড়িৎচালক বল \( 10\;V \) ও অভ্যন্তরীণ রোধ \( 1\;\Omega \)। কোশটিকে \( R=9\;\Omega \) রোধের সঙ্গে যুক্ত করা হল। \( 1\;C \) ধনাত্মক আধানকে \( R \) রোধের মধ্য দিয়ে ও কোশের মধ্য দিয়ে নিয়ে যেতে কোশ কত কার্য করবে?
কোশের তড়িৎচালক বল \( \left(E\right)=10\;V \) ও অভ্যন্তরীণ রোধ \( \left(r\right)=1\;\Omega \), বহির্বর্তনীর রোধ \( \left(R\right)=9\;\Omega \)।
বর্তনীতে প্রবাহমাত্রা,
\( I=\frac E{R+r} \\\)বা, \( I=\frac{10}{9+1} \)
বা, \( I=1\;A \)
\( R \) রোধের দু-প্রান্তের বিভবপ্রভেদ,
\( V=IR=1\;A\times9\;\Omega=9\;V \\\)ও নষ্ট ভোল্ট \( =Ir=1\;A\times1\;\Omega=1\;V \)
\( R \) রোধের মধ্য দিয়ে ও কোশের মধ্য দিয়ে \( 1\;C \) ধনাত্মক আধানকে নিয়ে যেতে কোশ দ্বারা কৃত কার্য যথাক্রমে \( W_1 \) ও \( W_2 \) হলে, \( W_1=9\;V\times1\;C=9\;J \) ও \( W_2=1\;V\times1\;C=1\;J \)।
একটি পদার্থের রোধাঙ্ক \( 9\times10^{-6}\;\Omega\cdot cm \)। ওই পদার্থের \( 0.5\;cm^2 \) প্রস্থচ্ছেদের ক্ষেত্রফলবিশিষ্ট কোনো তারের কত দৈর্ঘ্যের রোধ \( 0.5\;\Omega \) হবে।
তারের প্রস্থচ্ছেদের ক্ষেত্রফল \( \left(A\right)=0.5\;cm^2 \), উপাদানের রোধাঙ্ক \( \left(\rho\right)=9\times10^{-6}\;\Omega\cdot cm \) ও রোধ \( \left(R\right)=0.5\;\Omega \)।
মনে করি, তারের দৈর্ঘ্য \( l \)।
∴ \( R=\rho\frac lA \)
বা, \( l=\frac{RA}\rho \)
বা, \( l=\frac{0.5\times0.5}{9\times10^{-6}}=27777.7\;cm \)
বা, \( l=277.78\;m \) (প্রায়)
∴ ওই পদার্থের \( 0.5\;cm^2 \) প্রস্থচ্ছেদের ক্ষেত্রফলবিশিষ্ট কোনো তারের \( 277.78\;m \) (প্রায়) দৈর্ঘ্যের রোধ \( 0.5\;\Omega \) হবে।
দুটি ধাতব তারের দৈর্ঘ্য, ব্যাসার্ধ ও রোধাঙ্ক-প্রত্যেকটির অনুপাত 1 : 2 হলে তার দুটির রোধের অনুপাত কত?
মনে করি, প্রথম ও দ্বিতীয় তারের দৈর্ঘ্য, ব্যাসার্ধ ও রোধাঙ্ক যথাক্রমে \(l_{1,}\;r_{1,\;}\rho_1\) ও \( l_{2,}\;r_{2,\;}\rho_2 \)।
∴ \( \frac{l_1}{l_2}=\frac{r_1}{r_2}=\frac{\rho_1}{\rho_2}=\frac12 \)
তার দুটির প্রস্থচ্ছেদের ক্ষেত্রফল ও রোধ যথাক্রমে \( A_{1,\;}R_1 \) ও \( A_{2,\;}R_2 \) হলে,
\( \frac{R_1}{R_2}=\frac{\rho_1{\displaystyle\frac{l_1}{A_1}}}{\rho_2{\displaystyle\frac{l_2}{A_2}}}\)\(=\frac{\rho_1}{\rho_2}\times\frac{l_1}{l_2}\times\frac{A_2}{A_1}\)\(=\frac12\times\frac12\times\frac{\pi r_2^2}{\pi r_1^2}\)\(=\frac14\times\left(\frac{r_2}{r_1}\right)^2\)\(=\frac14\times2^2=1\\\)∴ তার দুটির রোধের অনুপাত হবে 1 : 1
\( 9\;g/cm^3 \) ঘনত্ববিশিষ্ট \( 10\;g \) ভরের একটি তামার তারের দৈর্ঘ্য ও প্রস্থচ্ছেদের ক্ষেত্রফল কত হলে তারটির রোধ \( 2\;\Omega \) হবে? ধরে নাও তামার রোধাঙ্ক, \( \rho=1.8\times10^{-6}\;\Omega\cdot cm \)।
তামার তারের রোধ \( \left(R\right)=2\;\Omega \), রোধাঙ্ক, \( \left(\rho\right)=1.8\times10^{-6}\;\Omega\cdot cm \)।
মনে করি, তারের দৈর্ঘ্য \( =l \) ও প্রস্থচ্ছেদের ক্ষেত্রফল \( =A \)
∴ \( R=\rho\frac lA \)
বা, \( 2=1.8\times10^{-6}\cdot\frac lA \)
বা, \( A=0.9\times10^{-6}\;l \)
তারের ভর \( \left(m\right)=10\;g \) ও ঘনত্ব \( \left(d\right)=9\;g/cm^3 \)
∴ তারের আয়তন, \( V=\frac md \)
বা, \( lA=\frac{10}9 \)
বা, \( l\times0.9\times10^{-6}\cdot l=\frac{10}9 \)
বা, \( l=\frac{10^4}9 \)
বা, \( l=1111.11\;cm=11.11\;m \) (প্রায়)
এবং \( A=0.9\times10^{-6}\;l \)
\(=0.9\times10^{-6}\times\frac{10^4}9\;cm^2\)\(=10^{-3}\;cm^2\)
∴ তামার তারের দৈর্ঘ্য ও প্রস্থচ্ছেদের ক্ষেত্রফল যথাক্রমে \( 11.11\;m \) ও \( 10^{-3}\;cm^2 \)
R রোধের একটি তারকে গলিয়ে ওই ধাতু দিয়ে ওর অর্ধেক দৈর্ঘ্যের একটি তার তৈরি করা হল। নতুন তারটির রোধ কত হবে?
মনে করি, মূল তারটির দৈর্ঘ্য \( =l \) ও প্রস্থচ্ছেদের ক্ষেত্রফল \( =A \)। তারের উপাদানের রোধাঙ্ক \( =\rho \) হলে, তারটির রোধ, \( R=\rho\frac lA \)।
তারটিকে গলানোর পর যে নতুন তার তৈরি করা হল তার দৈর্ঘ্য, \( l_1=\frac l2 \)।
মনে করি, নতুন তারটির প্রস্থচ্ছেদের ক্ষেত্রফল \( =A \)।
যেহেতু তারটির আয়তন অপরিবর্তিত আছে, সেহেতু,
\( l_1A_1=lA \\\)বা, \( \frac l2\cdot A_1=l\cdot A \)
বা, \( A_1=2A \)
∴ নতুন তারটির রোধ, \( R_1=\rho\frac{l_1}{A_1} \)
বা, \( R_1=\rho\cdot\frac{\displaystyle\frac l2}{2A} \)
বা, \( R_1=\frac14\times\frac{\rho l}A \)
বা, \( R_1=\frac R4 \)
∴ নতুন তারটির রোধ \( \frac R4 \) হবে।
একই উপাদান ও একই দৈর্ঘ্যের দুটি তারের প্রথমটির ব্যাসার্ধ দ্বিতীয়টির দ্বিগুণ। দ্বিতীয় তারের রোধ R হলে প্রথমটির রোধ কত?
মনে করি, দ্বিতীয় তারের ব্যাসার্ধ \( =r \)।
∴ প্রস্থচ্ছেদের ক্ষেত্রফল, \( A=\pi r^2 \)
উভয় তারের দৈর্ঘ্য \( =l \) ও তারের উপাদানের রোধাঙ্ক \( =\rho \) হলে, দ্বিতীয় তারের রোধ, \( R=\rho\cdot\frac lA \)।
এখন, প্রথম তারের ব্যাসার্ধ, \( r_1=2r \)
∴ প্রস্থচ্ছেদের ক্ষেত্রফল, \( A_1=\pi r_1^2 \)
বা, \( A_1=4\mathrm{πr}^2 \)
বা, \( A_1=4\mathrm A \)
∴ প্রস্থচ্ছেদের ক্ষেত্রফল, \( A_1=4\mathrm A \)
∴ প্রথম তারের রোধ, \( {\mathrm R}_1=\mathrm\rho\frac{\mathrm l}{{\mathrm A}_l} \)
বা, \( {\mathrm R}_1=\mathrm\rho\frac{\mathrm l}{4\mathrm A} \)
বা, \( {\mathrm R}_1=\frac{\mathrm R}4 \)
∴ প্রথম তারের রোধ, \( {\mathrm R}_1=\frac{\mathrm R}4 \)
একটি তামার খণ্ড থেকে 5 mm ব্যাসযুক্ত একটি তার প্রস্তুত করা হল। একই ভরের অন্য একখণ্ড তামা থেকে 1 cm ব্যাসের অপর একটি তার প্রস্তুত করা হল। তার দুটির রোধের অনুপাত কত?
প্রথম তারের ব্যাস \( \left(d_1\right)=5\;mm=0.5\;cm \)।
∴ প্রথম তারের প্রস্থচ্ছেদের ক্ষেত্রফল \( \left(A_1\right)=\frac{\pi d_1^2}4 \)
দ্বিতীয় তারের ব্যাস \( \left(d_2\right)=1\;cm \)
∴ দ্বিতীয় তারের প্রস্থচ্ছেদের ক্ষেত্রফল \( \left(A_2\right)=\frac{\pi d_2^2}4 \)
মনে করি, তার দুটির দৈর্ঘ্য যথাক্রমে \( l_1 \) ও \( l_2 \)।
উভয় তারের ভর সমান তাই আয়তনও সমান হবে।
∴ \(A_1l_1=A_2l_2 \)
বা, \( \frac{\pi d_1^2}4\cdot l_1=\frac{\pi d_2^2}4\cdot l_2 \)
বা, \( \frac{l_1}{l_2}=\left(\frac{d_2}{d_1}\right)^2 \)
বা, \( \frac{l_1}{l_2}=\left(\frac1{0.5}\right)^2 \)
বা, \( \frac{l_1}{l_2}=4 \)
তামার রোধাঙ্ক \( =\rho \) এবং তার দুটির রোধ যথাক্রমে \( R_1 \) ও \( R_2 \) হলে, \( R_1=\rho\frac{l_1}{A_1} \) ও \( R_2=\rho\frac{l_2}{A_2} \)
∴ \( \frac{R_1}{R_2}=\frac{\rho{\displaystyle\frac{l_1}{A_1}}}{\rho{\displaystyle\frac{l_2}{A_2}}} \\\)
বা, \( \frac{R_1}{R_2}=\frac{l_1}{l_2}\times\frac{A_2}{A_1} \)
বা, \( \frac{R_1}{R_2}=4\times\left(\frac{d_2}{d_1}\right)^2 \)
বা, \( \frac{R_1}{R_2}=4\times\left(\frac1{0.5}\right)^2 \)
বা, \( \frac{R_1}{R_2}=16 \)
∴ তার দুটির রোধের অনুপাত 16 : 1
\( 1\;\Omega,\;2\;\Omega \) ও \( 3\;\Omega \) মানের তিনটি রোধ সমান্তরাল সমবায়ে যুক্ত। তুল্য রোধ নির্ণয় করো।
মনে করি, তুল্য রোধ \( =R \)
∴ \( \frac1R=1+\frac12+\frac13 \)
বা, \( \frac1R=\frac{6+3+2}6 \)
বা, \( \frac1R=\frac{11}6 \)
বা, \( \frac1R=\frac6{11}\Omega \)
∴ তুল্য রোধ \( \frac6{11}\Omega \)
দুটি রোধের সমান্তরাল সমবায়ের তুল্য রোধ \( 2.4\;\Omega \)। একটি রোধ \( 4\;\Omega \) হলে অপর রোধটির মান কত?
মনে করি, অপর রোধটি \( =R \)
∴ \( \frac1{2.4}=\frac14+\frac1R \)
বা, \( \frac1R=\frac1{2.4}-\frac14\)
বা, \(\frac1R=\frac{10}{24}-\frac14\)
বা, \(\frac1R=\frac5{12}-\frac14\)
বা, \(\frac1R=\frac{5-3}{12}\)
বা, \(\frac1R=\frac2{12}\)
বা, \(\frac1R=\frac16\)
বা, \( R=6\;\Omega \)
∴ অপর রোধটির মান \( 6\;\Omega \)।
দুটি রোধের শ্রেণি সমবায় ও সমান্তরাল সমবায়ের তুল্য রোধ যথাক্রমে \( 9\;\Omega \) ও \( 2\;\Omega \)। রোধ দুটির মান নির্ণয় করো।
মনে করি, রোধ দুটির মান \( R_1 \) ও \( R_2 \)। রোধ দুটির শ্রেণি সমবায়ের তুল্য রোধ \( 9\;\Omega \)।
∴ \( R_1+R_2=9 \)
বা, \( R_2=9-R_1 \) ___(1)
আবার রোধ দুটির সমান্তরাল সমবায়ের তুল্য রোধ \( 2\;\Omega \)।
∴ \( \frac{R_1R_2}{R_1+R_2}=2 \)
বা, \( \frac{R_1\left(9-R_1\right)}9=2 \)
বা, \( 9R_1-R_1^2=18 \)
বা, \( R_1^2-9R_1+18=0 \)
বা, \( \left(R_1-3\right)\left(R_1-6\right)=0 \)
এখন \( R_1-3=0 \) হলে, \( R_1=3\;\Omega \)
∴ \( R_2=9-3=6\;\Omega \)
আবার \( R_1-6=0 \) হলে, \( R_1=6\;\Omega \)
∴ \( R_1=9-6=3\;\Omega \)
∴ রোধদুটির মান হল \( \;3\;\Omega,6\;\Omega \)।
\( 10\;\Omega \) রোধবিশিষ্ট একটি তারকে সমান দু-ভাগে ভাগ করে সমান্তরাল সমবায়ে যুক্ত করা হল। সমবায়টির রোধ কত?
তারের রোধ \( \left(R\right)=10\;\Omega \)। তারটিকে সমান দু-ভাগে ভাগ করলে প্রতিটি অংশের রোধ হবে, \( R_1=\frac{10}2=5\;\Omega \)।
এবার \( 5\;\Omega \) –এর দুটি রোধকে সমান্তরাল সমবায়ে যুক্ত করলে যদি তুল্য রোধ \( R_p \) হয় তবে
\( \frac1{R_p}=\frac15+\frac15 \\\)বা, \( \frac1{R_p}=\frac25 \)
বা, \( R_p=\frac52=2.5\;\Omega \)
∴ সমবায়টির রোধ \( 2.5\;\Omega \)।
\( 27\;\Omega \) রোধবিশিষ্ট একটি তারকে সমান তিনভাগে ভাগ করে সমান্তরাল সমবায়ে যুক্ত করা হল। সমবায়টির রোধ কত?
তারের রোধ \( \left(R\right)=27\;\Omega \)। তারটিকে সমান তিনভাগে ভাগ করলে প্রতিটি অংশের রোধ হবে, \( R_1=\frac R3=\frac{27}3=9\;\Omega \)
এবার \( 9\;\Omega \) -এর তিনটি রোধকে সমান্তরাল সমবায়ে যুক্ত করলে যদি তুল্য রোধ \( R_p \) হয় তবে,
\( \frac1{R_p}=\frac1{R_1}+\frac1{R_1}+\frac1{R_1}\\\)বা, \( \frac1{R_p}=\frac{1+1+1}{R_1} \)
বা, \( \frac1{R_p}=\frac3{R_1} \)
বা, \( R_p=\frac{R_1}3 \)
বা, \( R_p=\frac93=3\;\Omega \)
∴ সমবায়টির রোধ \( 3\;\Omega \)।
\( R \) মানের 3টি রোধের শ্রেণি সমবায় ও সমান্তরাল সমবায়ের তুল্য রোধ যথাক্রমে \( R_s \) ও \( R_P \) হলে \( \frac{R_s}{R_P} \) –এর মান কত?
রোধ তিনটির শ্রেণি সমবায়ের তুল্য রোধ,
\( R_s=R+R+R=3R \) ___(1)
এবং সমান্তরাল সমবায়ের ক্ষেত্রে,
\( \frac1{R_P}=\frac1R+\frac1R+\frac1R\\ \)বা, \( \frac1{R_P}=\frac3R \)
বা, \( R_P=\frac R3 \) ___(2)
∴ \( \frac{R_s}{R_P}=\frac{3R}{\displaystyle\frac R3}=9 \)
∴ \( \frac{R_s}{R_P} \) –এর মান \(9 \)
চিত্রে প্রদর্শিত বর্তনীতে A ও B বিন্দুর মধ্যে তুল্য রোধ নির্ণয় করো।
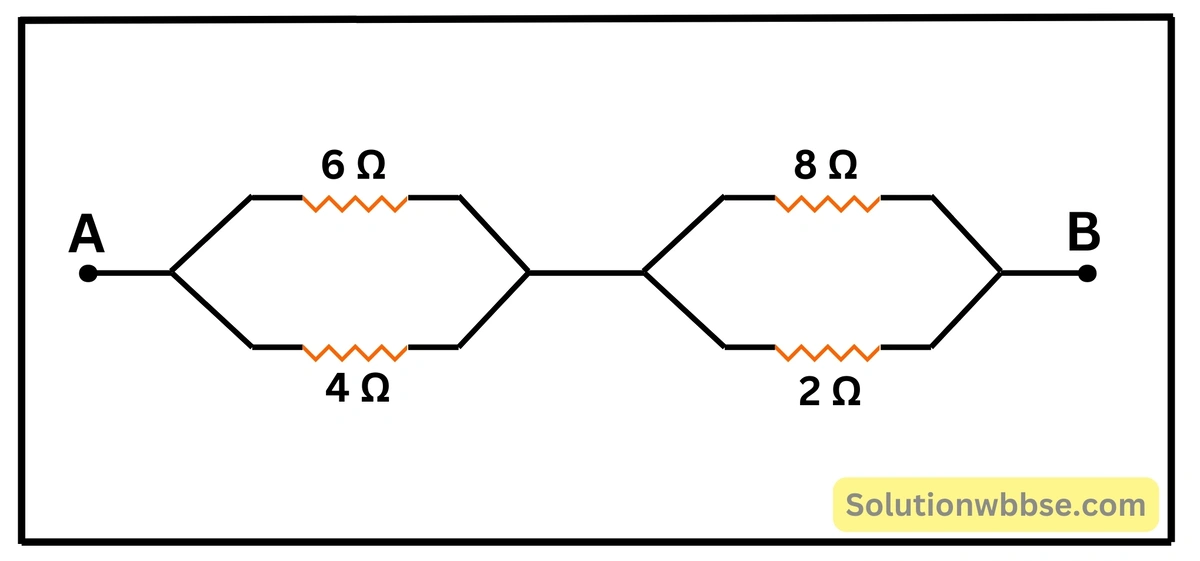
\(6\;\Omega \) ও \(4\;\Omega \) রোধদুটির সমান্তরাল সমবায়ের তুল্য রোধ,
\(R_1=\frac{6\times4}{6+4}=\frac{24}{10}=2.4\;\Omega\\ \)আবার \(8\;\Omega \) ও \(2\;\Omega \) রোধ দুটির সমান্তরাল সমবায়ের তুল্য রোধ,
\(R_2=\frac{8\times2}{8+2}=\frac{16}{10}=1.6\;\Omega \\\)এখন \(R_1 \) ও \(R_2 \) রোধ দুটি শ্রেণি সমবায়ে যুক্ত।
∴ \(R_1 \) ও \(R_2 \) রোধ দুটির শ্রেণি সমবায়ের তুল্য রোধ,
\(R=R_1+R_2=2.4\;\Omega+1.6\;\Omega=4\;\Omega\\ \)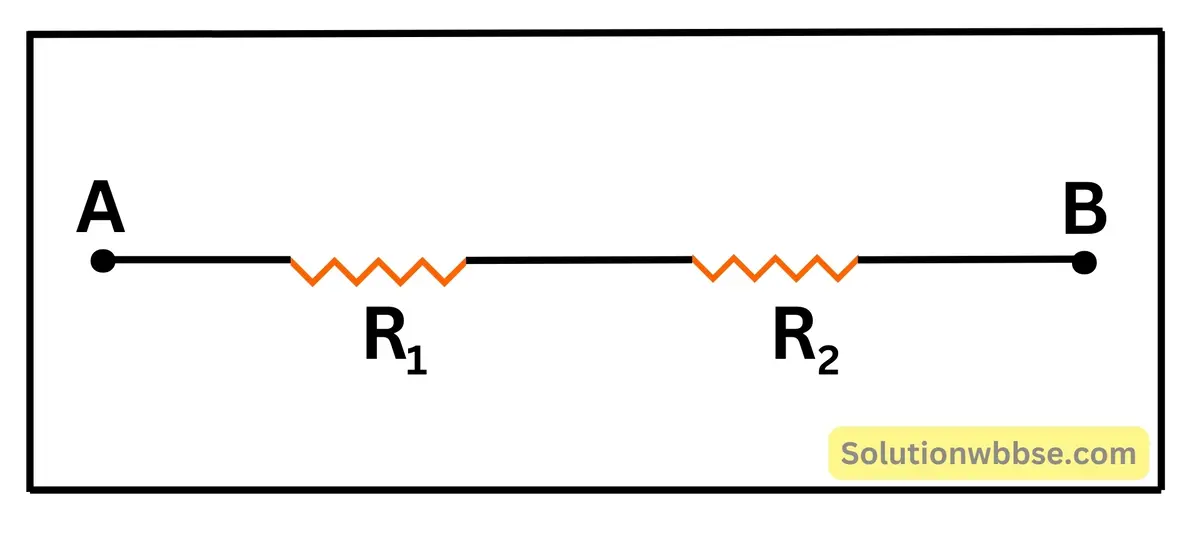
∴ \(A \) ও \(B \) বিন্দু দুটির মধ্যে তুল্য রোধ হল \( 4\;\Omega \)।
চিত্রে প্রদর্শিত বর্তনীতে \( I \) -এর মান নির্ণয় করো।
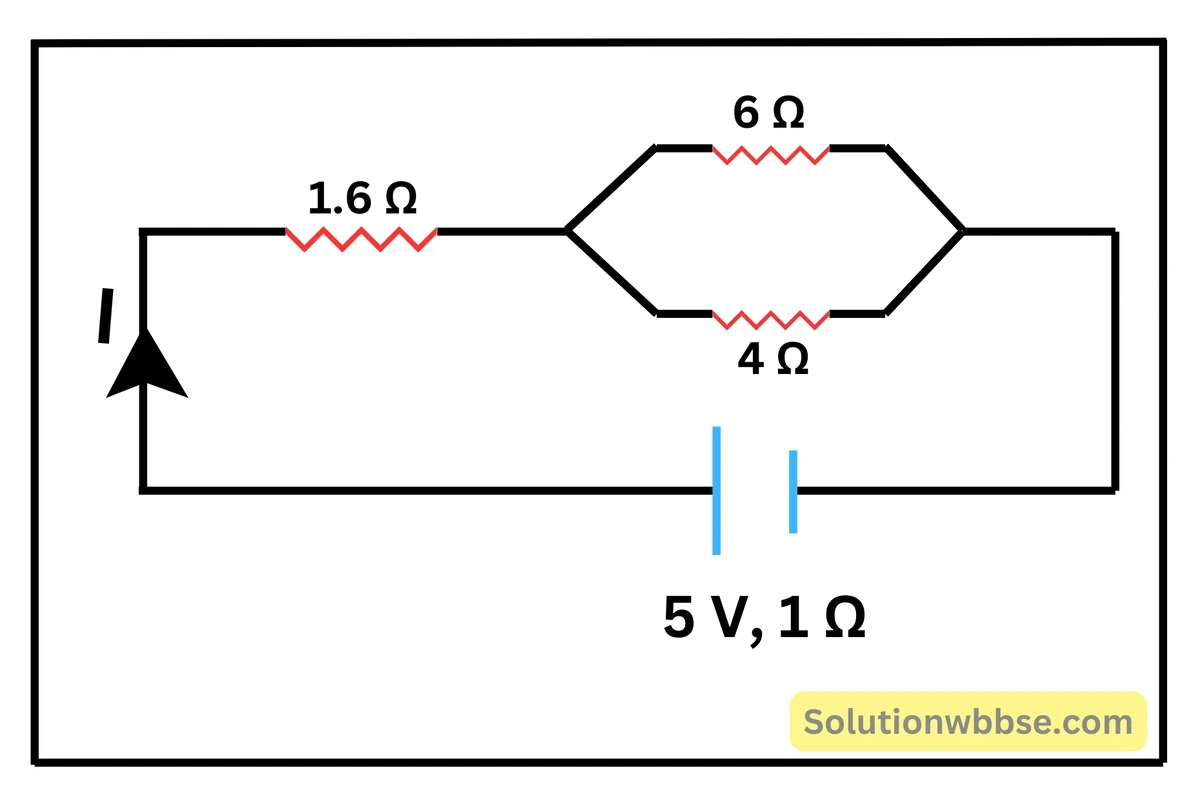
\(6\;\Omega \) ও \(4\;\Omega \) রোধদুটির সমান্তরাল সমবায়ের তুল্য রোধ \(R_1 \) হলে,
\( \frac1{R_1}=\frac16+\frac14 \\\)বা, \( \frac1{R_1}=\frac{2+3}{12} \)
বা, \( \frac1{R_1}=\frac5{12} \)
বা, \( \frac1{R_1}=\frac{12}5=2.4\;\Omega \)
\( {R_1} \) ও \( 1.6\;\Omega \) রোধ দুটি শ্রেণীর সমবায়ের তুল্য রোধ,
\( R=2.4+1.6=4\;\Omega\\ \)কোশের তড়িৎচালক বল \( \left(E\right)=5\;V \), অভ্যন্তরীণ রোধ \( \left(r\right)=1\;\Omega \)
\(∴ I=\frac E{R+r}\\ \)বা, \( I=\frac5{4+1} \)
বা, \( I=\frac55 \)
বা, \( I=1\;A \)
∴ প্রদর্শিত বর্তনীতে \( I \) -এর মান \( 1\;A \)
তড়িৎপ্রবাহের তাপীয় ফল ও তড়িৎক্ষমতা
\( 10\;\Omega \) রোধের ভিতর দিয়ে \( 1\;minute \) ধরে \( 0.8\;A \) তড়িৎপ্রবাহ হলে কত তাপ উৎপন্ন হবে?
পরিবাহীর রোধ \( \left(R\right)=10\;\Omega \), তড়িৎপ্রবাহ \( \left(I\right)=0.8\;A \) ও তড়িৎপ্রবাহের সময় \( \left(t\right)=1\;minute=60\;s \)
∴ পরিবাহীতে উৎপন্ন তাপ,
\( H=I^2Rt \\\)বা, \( H=0.8^2\times10\times60 \)
বা, \( H=384\;J \)
বা, \( H=\frac{384}{4.2}cal \)
বা, \( H=91.42\;cal \)
∴ তড়িৎপ্রবাহ হলে \( 91.42\;cal \) তাপ উৎপন্ন হবে।
একটি ক্যালোরিমিটারে \( 1.5\;kg \) তেল (আপেক্ষিক তাপ \( =0.6\;cal\cdot g^{-1}\cdot^\circ C^{-1} \)) নেওয়া হল এবং \( 3\;\Omega \) -এর একটি কুণ্ডলীকে তার মধ্যে ডুবিয়ে কুণ্ডলীতে \( 3\;A \) প্রবাহমাত্রা পাঠানো হল। ক্যালোরিমিটারে তেলের উষ্ণতা \( 10^\circ C \) বাড়াতে কত সময় ধরে তড়িৎপ্রবাহ পাঠাতে হবে? ধরে নাও ক্যালোরিমিটার কোনো তাপ গ্রহণ করেনি। \( J=4.2\;/cal \)
তেলের ভর \( \left(m\right)=1.5\;kg=1500\;g \), তেলের আপেক্ষিক তাপ \( \left(s\right)=0.6\;cal\cdot g^{-1}\cdot^\circ C^{-1} \) ও তেলের উষ্ণতা বৃদ্ধি \( \left(\theta\right)=10^\circ C \)।
তেল দ্বারা গৃহীত তাপ, \( H_1=ms\theta \)
বা, \( H_1=1500\times0.6\times10 \)
বা, \( H_1= 9000\;cal \)
আবার কুণ্ডলীর রোধ \( \left(R\right)=3\;\Omega \), কুণ্ডলীর মধ্য দিয়ে প্রবাহমাত্রা \( \left(I\right)=3\;A \)।
মনে করি, কুণ্ডলীর মধ্য দিয়ে \( t \) সময় ধরে তড়িৎপ্রবাহ পাঠাতে হবে।
∴ কুণ্ডলীতে উৎপন্ন তাপ, \( H_2=\frac{I^2Rt}J \)
বা, \( H_2=\frac{3^2\times3\times t}{27} \)
বা, \( H_2=\frac{27t}{4.2}cal \)
শর্তানুসারে, \( H_1=H_2 \)
বা, \( 9000=\frac{27t}{4.2} \)
বা, \( 27t=9000\times4.2 \)
বা, \( t=\frac{9000\times4.2}{27} \)
বা, \( t=1400\;s \)
বা, \( t=23\;minute\;20\;s \)
∴ ক্যালোরিমিটারে তেলের উষ্ণতা \( 10^\circ C \) বাড়াতে \(23\;minute\;20\;s \) সময় ধরে তড়িৎপ্রবাহ পাঠাতে হবে।
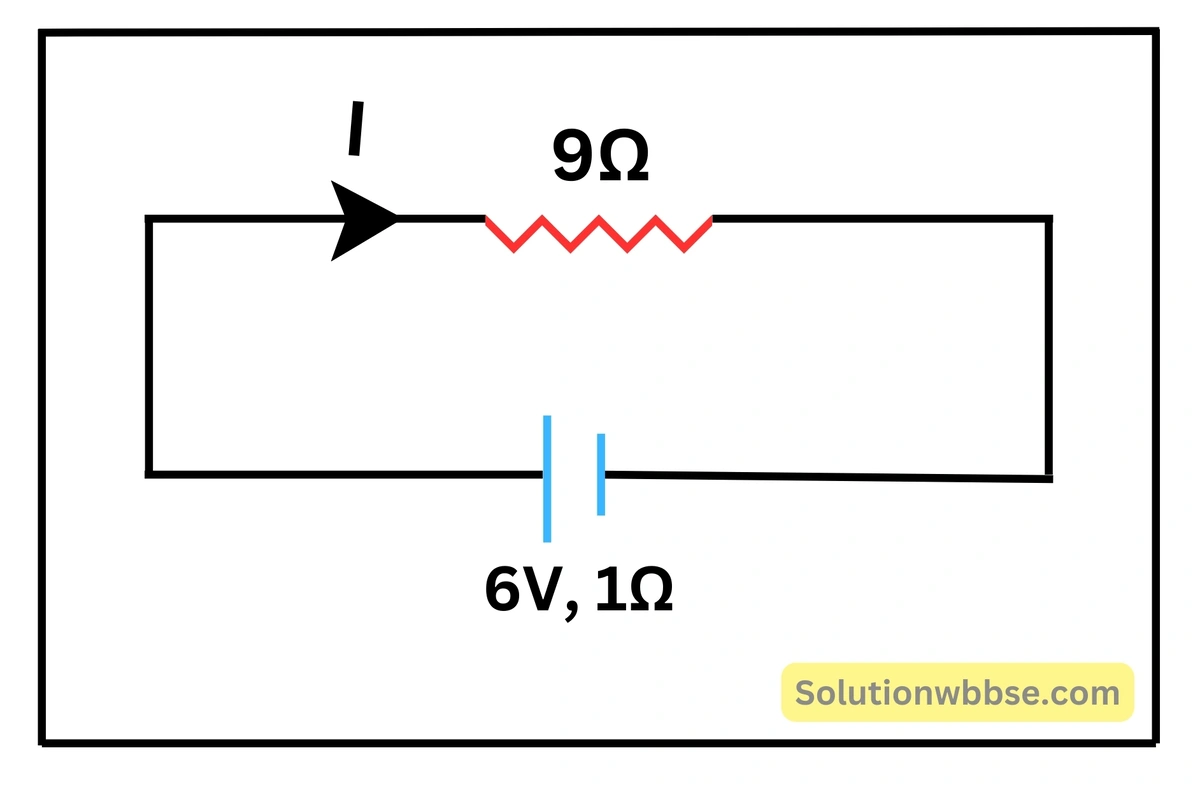
একটি তড়িৎকোশের তড়িৎচালক বল \( 6\;V \) ও অভ্যন্তরীণ রোধ \( 1\;\Omega \)। তড়িৎকোশটিকে \( 9\;\Omega \) -এর একটি রোধের সঙ্গে যুক্ত করা হল। রোধটিতে \( 21\;s \) সময়ে কত তাপ উৎপন্ন হবে?
তড়িৎকোশের তড়িৎচালক বল \( \left(E\right)=6\;V \) ও অভ্যন্তরীণ রোধ \( \left(r\right)=1\;\Omega \)।
বহির্বর্তনীর রোধ \( \left(R\right)=9\;\Omega \)
∴ বর্তনীতে তড়িৎপ্রবাহ,
\( I=\frac E{R+r} \\\)বা, \( I=\frac6{9+1} \)
বা, \( I=0.6\;A \)
\( t=21\;s \) সময়ে \( R \) রোধে উৎপন্ন তাপ,
\( H=\frac{I^2Rt}{4.2} \\\)বা, \( H=\frac{0.6^2\times9\times21}{4.2} \)
বা, \( H=16.2\;cal \)
∴ রোধটিতে \( 21\;s \) সময়ে \( 16.2\;cal \) তাপ উৎপন্ন হবে।
সমান রোধবিশিষ্ট দুটি পরিবাহীর মধ্য দিয়ে একই সময়ের জন্য তড়িৎ পাঠালে দ্বিতীয় তারে উৎপন্ন তাপ প্রথম তারের 16 গুণ হয়। পরিবাহী দুটিতে তড়িৎপ্রবাহের অনুপাত নির্ণয় করো।
মনে করি, প্রথম ও দ্বিতীয় তারে তড়িৎপ্রবাহ যথাক্রমে \( I_1 \) ও \( I_2 \)।
উভয় পরিবাহীর রোধ ও তড়িৎপ্রবাহের সময় যথাক্রমে \( R \) ও \( t \) হলে, প্রথম পরিবাহীতে উৎপন্ন তাপ, \( H_1=\frac{I_1^2Rt}{4.2}cal \) এবং দ্বিতীয় পরিবাহীতে উৎপন্ন তাপ, \( H_2=\frac{I_2^2Rt}{4.2}cal \)
শর্তানুসারে, \( H_2=16H_1 \)
বা, \( \frac{I_2^2Rt}{4.2}=16\times\frac{I_1^2Rt}{4.2} \)
বা, \( I_2^2=16I_1^2 \)
বা, \( I_2=4I_1 \)
বা, \( \frac{I_1}{I_2}=\frac14 \)
∴ পরিবাহী দুটিতে তড়িৎপ্রবাহের অনুপাত 1 : 4
একটি বাড়িতে \( 6\)টি \( 40\;W \) -এর বাতি, \( 4 \)টি \( 80\;W \) -এর পাখা, একটি \( 100\;W \) -এর \( TV \) দৈনিক \( 5\;h \) করে চলে। \( 30 \) দিনের মাসে ওই বাড়ির মাসিক শক্তি ব্যয় কত \( BOT \) হবে?
\( 1\;kW\cdot h=1\;BOT=1 \) ইউনিট।
বাতি, পাখা ও TV প্রত্যেকটি দৈনিক 5 h করে চলে।
ব্যয়িত ক্ষমতা \( =40\times6+80\times4+100=660\;W \)
একদিনে ব্যয়িত তড়িৎশক্তি
\( =660\;W\times5\;h\\ \)\( =3300\;W\cdot h \\\)\(=\frac{3300}{1000}kW\cdot h\\\)\(=3.3\;BOT\\\)∴ 30 দিনের মাসে ব্যয়িত তড়িৎশক্তি \( =3.3\times30=99\;BOT \)
একটি বাড়িতে \( 1 \)টি \( 60\;W \) ও \( 2 \)টি \( 100\;W \) -এর বৈদ্যুতিক বাতি, \( 1 \)টি \( 80\;W \) -এর পাখা এবং \( 1 \)টি \( 1000\;W \) -এর হিটার আছে। যদি মে মাসে প্রতিদিন প্রত্যেক বাতি \( 6\;h \) করে জ্বলে, পাখা \( 12\;h \) চলে এবং হিটার \( 4\;h \) চলে তবে ওই মাসের বিদ্যুৎ বিল কত হবে? \( 1\;BOT \) -এর মূল্য \( 5 \) টাকা।
মে মাস 31 দিনের।
বৈদ্যুতিক বাতি, পাখা ও হিটারের জন্য প্রতিদিন ব্যয়িত তড়িৎশক্তি
= \( \left(1\times60\times6+2\times100\times6+1\times80\times12+1\times1000\times4\right)\;W\cdot h\)
\(= 6520\;W\cdot h\\ \)\(=6.52\;kW\cdot h\\ \)\(=6.52\;BOT\\ \)∴ মে মাসে ব্যয়িত তড়িৎশক্তি \( = 6.52\times31=202.12\;BOT \)
অর্থাৎ মে মাসে বিদ্যুৎ বিল \( =202.12\times5=1010.60 \) টাকা।
একটি তড়িৎকোশকে পরপর দুটি বহিস্থ রোধ \( R \) ও \( S \) -এর সঙ্গে যুক্ত করা হল। যদি উভয় রোধে ব্যয়িত ক্ষমতা সমান হয় তাহলে কোশের অভ্যন্তরীণ রোধ নির্ণয় করো।
মনে করি, তড়িৎকোশের তড়িৎচালক বল \( =E \) ও অভ্যন্তরীণ রোধ \( =r \)।
তড়িৎকোশের সঙ্গে \( R \) রোধ যুক্ত করলে বর্তনীতে তড়িৎপ্রবাহ, \( I_1=\frac E{R+r} \)
আবার, তড়িৎকোশের সঙ্গে \( S \) রোধ যুক্ত করলে বর্তনীতে তড়িৎপ্রবাহ, \( I_2=\frac E{S+r} \)
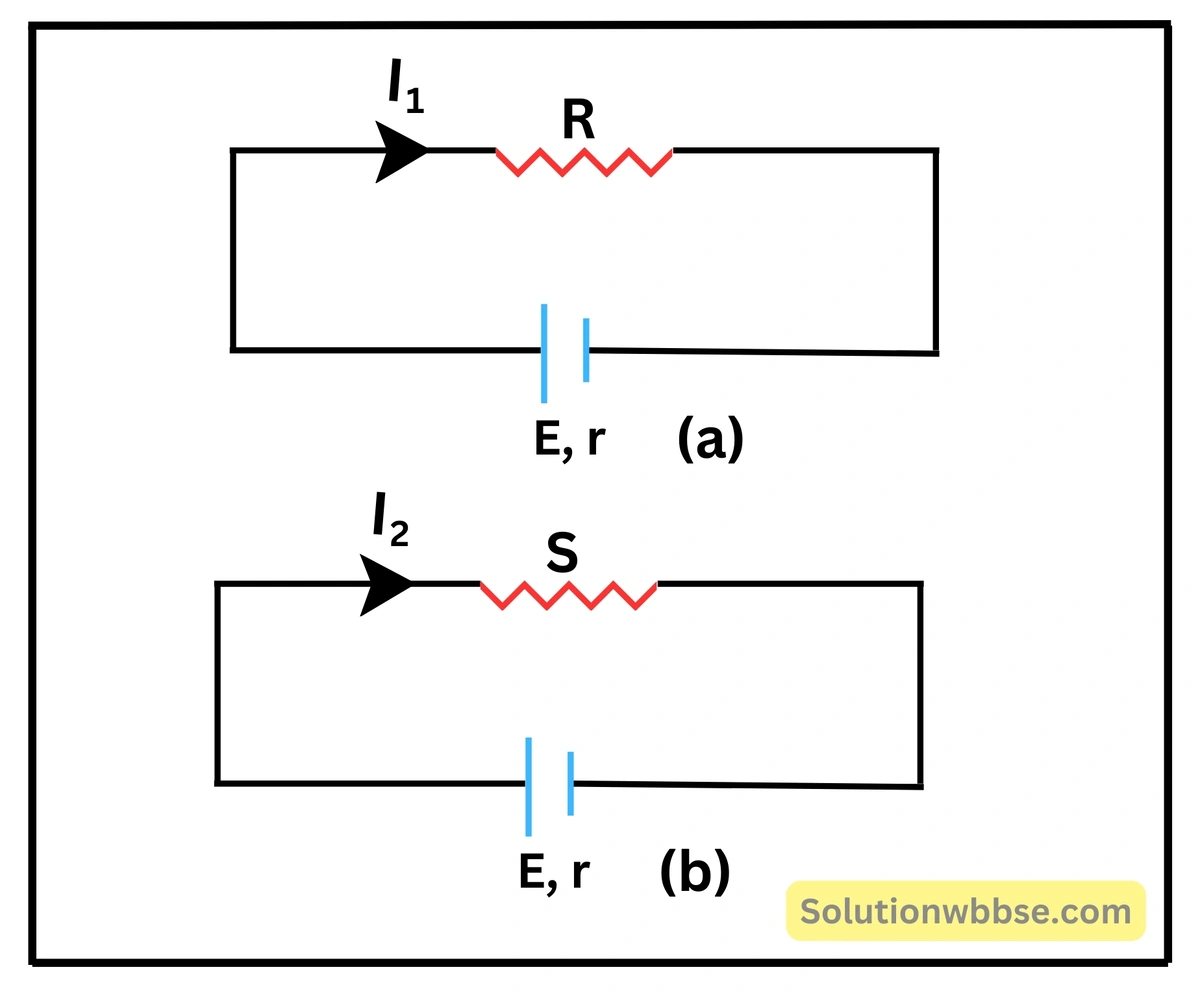
শর্তানুসারে, \( I_1^2R=I_2^2S \)
বা, \( I_1\cdot\sqrt R=I_2\cdot\sqrt S \)
বা, \( \frac{E\sqrt R}{R+r}=\frac{E\sqrt S}{S+r} \)
বা, \( \sqrt R\cdot S+\sqrt R\cdot r=R\cdot\sqrt S+r\cdot\sqrt S \)
বা, \( \sqrt R\cdot r-r\cdot\sqrt S=R\cdot\sqrt S-\sqrt R\cdot S \)
বা, \( r\left(\sqrt R-\sqrt S\right)=\sqrt{RS}\left(\sqrt R-\sqrt S\right) \)
বা, \( r=\sqrt{RS} \)
∴ যদি উভয় রোধে ব্যয়িত ক্ষমতা সমান হয় তাহলে কোশের অভ্যন্তরীণ রোধ \( \sqrt{RS} \) হবে।
একটি তড়িৎকোশের তড়িৎচালক বল \( 10\;V \), অভ্যন্তরীণ রোধ \( 1\;\Omega \)। তড়িৎকোশটিকে \( 3\;\Omega \) রোধের সঙ্গে যুক্ত করলে কোশের তাপ উৎপাদনের হার কত?
তড়িৎকোশের তড়িৎচালক বল \( \left(E\right)=10\;V \), অভ্যন্তরীণ রোধ \( \left(r\right)=1\;\Omega \)।
তড়িৎকোশটিকে \( 3\;\Omega \) রোধের সঙ্গে যুক্ত করলে বর্তনীতে তড়িৎপ্রবাহ, \( I=\frac E{R+r} \) যেখানে \( R=3\;\Omega \)।
বা, \( R=\frac{10}{3+1} \)
বা, \( I=2.5\;A \)
∴ কোশের তাপ উৎপাদনের হার
\(= I^2\left(R+r\right)\\\)\(=2.5^2\left(3+1\right)\\\)\(=25\;J/s\\\)\( =\frac{25}{4.2}cal/s \\\)\(=5.95\;cal/s \\\)∴ তড়িৎকোশটিকে \( 3\;\Omega \) রোধের সঙ্গে যুক্ত করলে কোশের তাপ উৎপাদনের হার \(5.95\;cal/s \)
একটি বাড়িতে শক্তি মিটারের রেটিং \( 220\;V-10\;A \)। ওই বাড়িতে সর্বাধিক কতগুলি \( 60\;W \) -এর বাতি একসঙ্গে জ্বালানো যাবে?
মনে করি, বাড়িতে সর্বাধিক \( x \)টি \( 60\;W \) -এর বাতি একসঙ্গে জ্বালানো যাবে।
বাড়িতে ব্যয়িত সর্বাধিক ক্ষমতা = \( 220\;V\times10\;A=2200\;W \)
শর্তানুসারে, \( 60x=2200 \)
বা, \( x=\frac{2200}{60} \)
বা, \( x=36.67 \)
∴ ওই বাড়িতে সর্বাধিক \( 36 \)টি বাতি জ্বালানো যাবে।
একটি পরিবাহী তারের দুই প্রান্তে বিভবপ্রভেদ একই রেখে দৈর্ঘ্য ও ব্যাসার্ধ উভয়ই দ্বিগুণ করলে তাপ উৎপন্নের হারের কীরূপ পরিবর্তন হবে?
মনে করি, প্রথম ক্ষেত্রে তারের দৈর্ঘ্য \( =l \), ব্যাসার্ধ \(=r\)।
∴ প্রস্থচ্ছেদের ক্ষেত্রফল, \( A=\pi r^2 \)
তারের উপাদানের রোধাঙ্ক \( \rho \) হলে, তারের রোধ,
\( R=\rho\frac lA \\\)তারের দুই প্রান্তে বিভবপ্রভেদ \( =V \) হলে, তাপ উৎপন্নের হার,
\( H=\frac{V^2}{4.2R}cal/s \) ___(1)
দ্বিতীয় ক্ষেত্রে তারের দৈর্ঘ্য, \( \left(l_1\right)=2l \), ব্যাসার্ধ, \( \left(r_1\right)=2r\)
∴ প্রস্থচ্ছেদের ক্ষেত্রফল,
\( A_1=\pi r_1^2\\ \)বা, \( A_1=4\pi r^2 \)
বা, \( A_1=4A \)
এখন তারের রোধ,
\( R_1=\rho\frac{l_1}{A_1}\\ \)বা, \( R_1=\rho\cdot\frac{2l}{4A} \)
বা, \( R_1=\frac12\times\frac{\rho l}A \)
বা, \( R_1=\frac R2 \)
∴ এখন তাপ উৎপন্নের হার,
\( H_1=\frac{V^2}{4.2R_1} \\\)বা, \( H_1=\frac{2V^2}{4.2\times R} \)
বা, \( H_1=2H \) ___(2)
∴ দ্বিতীয় ক্ষেত্রে তাপ উৎপন্নের হার প্রথম ক্ষেত্রের তুলায় দ্বিগুণ হবে।
সমান্তরাল সমবায়ে যুক্ত দুটি রোধের অনুপাত \( X:Y \)। কোনো নির্দিষ্ট সময়ে ওই দুই রোধে উৎপন্ন তাপের অনুপাত কত?
মনে করি, রোধ দুটির মান যথাক্রমে \( R_1 \) ও \( R_2 \)।
∴ \( \frac{R_1}{R_2}=\frac xy \)
রোধ দুটি সমান্তরাল সমবায়ে যুক্ত, তাই উভয়ের প্রান্তীয় বিভবপ্রভেদ সমান হবে।
সমবায়ের দু-প্রান্তের বিভবপ্রভেদ \( V \) এবং \( t \) সময়ে \( R_1 \) ও \( R_2 \) রোধে উৎপন্ন তাপের পরিমাণ \( H_1 \) ও \( H_2 \) (\( J \) এককে) হলে, \( H_1=\frac{V^2}{R_1}t \) ও \( H_2=\frac{V^2}{R_2}t \)।
∴ \( \frac{H_1}{H_2}=\frac{{\displaystyle\frac{V^2}{R_1}}\cdot t}{{\displaystyle\frac{V^2}{R_2}}\cdot t} \)
বা, \( \frac{H_1}{H_2}=\frac{R_2}{R_1} \)
বা, \( \frac{H_1}{H_2}=\frac yx \)
∴ কোনো নির্দিষ্ট সময়ে ওই দুই রোধে উৎপন্ন তাপের অনুপাত \( H_1\;:\;H_2=y\;:\;x \)
220 V-100 W -এর একটি বাতি রোজ 6 h করে জ্বালানো হলে 30 দিনে কত বিদ্যুৎ বিল হবে? 1 BOT -এর মূল্য 5 টাকা।
একদিনে ব্যয়িত তড়িৎশক্তি \( =100\times6=600\;W\cdot h \)
∴ 30 দিনে ব্যয়িত তড়িৎশক্তি
\(=600\times30 \\\)= \(18000\;W\cdot h\)
= \(18\;kW\cdot h\)
= \(18\;BOT \) একক
∴ বিদ্যুৎ বিল হবে \( =5\times18=90 \) টাকা।
Class 10 Physical Science – Notes for All Chapters
আমরা আমাদের আর্টিকেলে দশম শ্রেণীর ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় ‘চলতড়িৎ’ এর কিছু গাণিতিক উদাহরণ নিয়ে আলোচনা করেছি। এই প্রশ্নগুলো দশম শ্রেণীর ভৌতবিজ্ঞান পরীক্ষার জন্য বা চাকরির পরীক্ষার জন্য অনেক গুরুত্বপূর্ণ। কারণ এই প্রশ্নগুলি দশম শ্রেণীর পরীক্ষা বা চাকরির পরীক্ষায় প্রায় দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা হলে, আপনারা আমাদের সাথে টেলিগ্রামে যোগাযোগ করতে পারেন, আমরা উত্তর দেওয়ার চেষ্টা করবো। তাছাড়া নিচে আমাদের এই পোস্টটি আপনার প্রিয়জনের সাথে শেয়ার করুন, যাদের এটি প্রয়োজন হতে পারে। ধন্যবাদ।






মন্তব্য করুন