আমরা আমাদের আর্টিকেলে দশম শ্রেণীর ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় ‘চলতড়িৎ’ এর সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর নিয়ে আলোচনা করবো। এই প্রশ্নগুলো দশম শ্রেণীর ভৌতবিজ্ঞান পরীক্ষার জন্য ও প্রতিযোগিতামূলক পরীক্ষার জন্য অনেক গুরুত্বপূর্ণ।

তড়িদাধান ও কুলম্বের সূত্র
তড়িদাধান কাকে বলে? এটি কয় প্রকার ও কী কী?
তড়িদাধান হল বস্তুর এমন এক ভৌত ধর্ম যার জন্য বস্তুটি কোনো তড়িদ্গ্রস্ত বা অনাহিত বস্তুকে বল প্রয়োগ করে। তড়িদাধান দুই প্রকার – ধনাত্মক আধান ও ঋণাত্মক আধান।
ঘর্ষণ দ্বারা কোনো বস্তুকে যখন তড়িদাহিত করা হয় তখন কোন্ বস্তুর আধান কেমন হয়?
একটি বস্তুকে যখন অন্য বস্তু দ্বারা ঘর্ষণ করা হয়, তখন একটি বস্তু থেকে কিছু ইলেকট্রন অন্য বস্তুটিতে স্থানান্তরিত হয়। যে বস্তুতে ইলেকট্রনের ঘাটতি হয় সেই বস্তুটি ধনাত্মক তড়িদ্গ্রস্ত ও যে বস্তুতে ইলেকট্রনের আধিক্য হয় সেই বস্তুটি ঋণাত্মক তড়িদ্গ্রস্ত হয়।
কোনো তড়িদ্গ্রস্ত বস্তু অন্য কোনো বস্তুকে কখন আকর্ষণ ও কখন বিকর্ষণ করে?
কোনো তড়িদ্গ্রস্ত বস্তু অন্য কোনো নিস্তড়িৎ বস্তুকে ও বিপরীতধর্মী আধানে আহিত বস্তুকে আকর্ষণ করে এবং সমজাতীয় আধানে আহিত বস্তুকে বিকর্ষণ করে।
কুলম্বের সূত্রটি লেখো।
কুলম্বের সূত্র – দুটি বিন্দু-আধানের মধ্যে পারস্পরিক আকর্ষণ বা বিকর্ষণ বল আধান দুটির গুণফলের সমানুপাতিক এবং আধান দুটির মধ্যবর্তী দূরত্বের বর্গের ব্যস্তানুপাতিক।
স্যার উইলিয়াম গিলবার্ট ধাতব দণ্ডকে আহিত করতে না পারায় কী সিদ্ধান্ত নেন?
স্যার উইলিয়াম গিলবার্ট কোনোভাবেই ধাতব দণ্ডকে আহিত করতে পারেননি। তিনি এই সিদ্ধান্তে উপনীত হন যে, ধাতুকে আহিত করা যায় না। এর প্রায় 100 বছর পর ডু ফে (Du Fay) দেখান এই ধারণা ভুল। ধাতব দণ্ডকে অন্তরক হাতলে ধরে ঘষলে তড়িদাহিত করা যায়।
কুলম্বের সূত্রের গাণিতিক রূপটি লেখো।
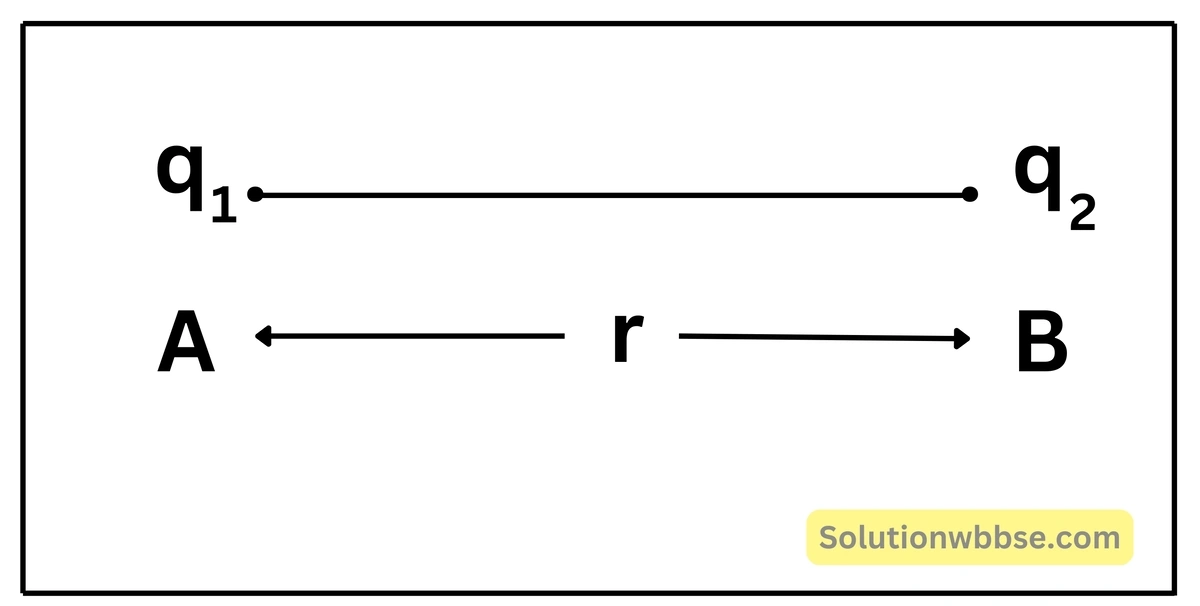
মনে করি, দুটি বিন্দু-আধান \( q_1 \) ও \( q_2 \) যথাক্রমে \( A \) ও \( B \) বিন্দুতে আছে । আধান দুটির ব্যবধান \( r \)। আধান দুটির মধ্যে পারস্পরিক বল \( F \) হলে, কুলম্বের সূত্রানুযায়ী,
\( F\propto q_1q_2 \) [যখন \( r \) স্থির] ও
\( F\propto\frac1{r^2} \) [যখন \( q_{1,}q_2 \) স্থির]
যৌগিক ভেদের সূত্রানুযায়ী,
\( F\propto\frac{q_1q_2}{r^2} \) [যখন \( q_{1,}q_{2,}r \) পরিবর্তনশীল]
বা, \( F=k\cdot\frac{q_1q_2}{r^2} \)
যেখানে k একটি ধ্রুবক যার মান পারিপার্শ্বিক মাধ্যম ও এককের পদ্ধতির ওপর নির্ভরশীল।
কুলম্বের সূত্রের সাহায্যে CGS পদ্ধতিতে একক আধানের সংজ্ঞা দাও।
\( q_1 \) ও \( q_2 \) দুটি বিন্দু-আধান \( r \) ব্যবধানে থাকলে যদি আধান দুটির মধ্যে পারস্পরিক বল \( F \) হয় তবে কুলম্বের সূত্র থেকে পাওয়া যায়, \( F=k\cdot\frac{q_1q_2}{r_2} \) যেখানে \( k \) একটি ধ্রুবক। আধান দুটি শূন্যস্থানে থাকলে CGS পদ্ধতিতে \( k=1 \) হয়।
∴ \( F=\frac{q_1q_2}{r^2} \) ___(1)
এখন \( q_1=q_2=q,\;r=1\;cm,\;F=1\;dyn \) হলে (1) নং সমীকরণ থেকে পাওয়া যায়,
\( q^2=1 \\\)বা, \( q=\pm1 \)
অর্থাৎ শূন্যস্থানে সমপ্রকৃতির ও সমমানের দুটি বিন্দু-আধান 1 cm ব্যবধানে থেকে যদি পরস্পরের ওপর 1 dyn বিকর্ষণ বল প্রয়োগ করে তবে প্রত্যেকটি আধানকে CGS পদ্ধতিতে একক আধান বা 1 esu আধান বা 1 স্ট্যাটকুলম্ব বলা হয়।
কুলম্বের সূত্রের সাহায্যে \( SI \) -তে একক আধানের সংজ্ঞা দাও।
\( q_1 \) ও \( q_2 \) দুটি বিন্দু-আধান \( r \) ব্যবধানে থাকলে যদি আধান দুটির মধ্যে পারস্পরিক বল \( F \) হয় তবে কুলম্বের সূত্র থেকে পাওয়া যায়, \( F=k\cdot\frac{q_1q_2}{r^2} \) , যেখানে \( k \) একটি ধ্রুবক। আধান দুটি শূন্যস্থানে থাকলে \( SI \) -তে \( k=9\times10^9 \) হয়।
∴ \( F=9\times10^9\frac{q_1q_2}{r^2} \) ___(1)
এখন \( q_1=q_2=q,\;r=1\;m,\;F=9\times10^9\;N \) হলে (1) নং সমীকরণ থেকে পাই,
\( 9\times10^9=9\times10^9\cdot q^2 \\\)বা, \( q^2=1 \)
বা, \( q=\pm1 \)
অর্থাৎ শূন্যস্থানে সমপ্রকৃতির ও সমমানের দুটি বিন্দু-আধান \( 1\;m \) ব্যবধানে থেকে যদি পরস্পরের ওপর \( 9\times10^9\;N \) বিকর্ষণ বল প্রয়োগ করে তবে প্রত্যেক আধানকে \( SI \) -তে একক আধান বা 1 C (কুলম্ব) বলা হয়।
আধানের \( SI \) ও \( CGS \) এককের মধ্যে সম্পর্ক স্থাপন করো।
\( SI \) -তে আধানের একক \( C \) (কুলম্ব) ও \( CGS \) পদ্ধতিতে আধানের একক \( esu \) আধান।
মনে করি, \(1\;C=x\;esu \) আধান।
∴ \(q_1=q_2=1\;C=x\;esu \) মানের দুটি বিন্দু-আধানকে \(r=1\;m=100cm \) ব্যবধানে রাখলে পারস্পরিক বিকর্ষণবল, \(F=9\times10^9\;N=9\times10^{14}\;dyn\)
∴ \( F=\frac{q_1q_2}{r^2} \) সমীকরণ থেকে পাওয়া যায়,
বা, \( 9\times10^{14}=\frac{x^2}{10^4} \)
বা, \( x^2=9\times10^{18} \)
বা, \( x=3\times10^9 \)
∴ \( 1\;C=3\times10^9\;esu \) আধান।
দুটি বিন্দু-আধানের পারস্পরিক বল সংক্রান্ত কুলম্বের সূত্রকে সর্বজনীন বলা যায় কি?
কোনো মাধ্যমে দুটি বিন্দু-আধান \( q_1 \) ও \( q_2 \) – কে ব্যবধানে রাখলে পারস্পরিক তাড়িতিক বল সংক্রান্ত কুলম্বের সূত্রের গাণিতিক রূপ হল, \( F=k\cdot\frac{q_1q_2}{r^2} \) , যেখানে \( k \) একটি ধ্রুবক। \( k \) ধ্রুবকটি মাধ্যমের প্রকৃতির ওপর নির্ভরশীল। সুতরাং দুটি বিন্দু-আধানের মধ্যে পারস্পরিক তাড়িতিক বল মাধ্যমের প্রকৃতির ওপর নির্ভরশীল এবং বিভিন্ন মাধ্যমে এই বলের মান বিভিন্ন। তাই কুলম্বের সূত্রকে সর্বজনীন বলা যায় না।
Q আধানকে দু-ভাগে ভাগ করে কিছুটা ব্যবধানে রাখা হল। কীভাবে ভাগ করা হলে পারস্পরিক বিকর্ষণ বল সর্বাধিক হবে?
মনে করি, \( Q \) আধানকে \( q \) ও \( \left(Q-q\right) \) দুটি অংশে ভাগ করে r ব্যবধানে রাখা হল।
∴ পারস্পরিক বিকর্ষণ বল,
\(F=k\frac{q\left(Q-q\right)}{r^2} \) [যেখানে, k একটি ধ্রুবক]
বা, \( F=\frac k{r^2}\left(Qq-q^2\right) \)
বা, \( F=\frac{-k}{r^2}\left(q^2-Qq\right) \)
বা, \( F=-\frac k{r^2}\left\{q^2-2q⋅\frac Q2+\left(\frac Q2\right)^2-\frac{Q^2}4\right\} \)
বা, \(F=-\frac k{r^2}\left\{\left(q-\frac Q2\right)^2-\frac{Q^2}4\right\}\)
বা, \(F=\frac k{r^2}\left\{\frac{Q^2}4-\left(q-\frac Q2\right)^2\right\}\)
\( F \) -এর সর্বোচ্চ মানের জন্য \(q-\frac Q2=0 \) হবে।
বা, \(q=\frac Q2 \)
∴ \(Q \) আধানকে সমান ভাগে বা \(\frac Q2 \) এবং \(\frac Q2\) অংশে ভাগ করে কিছুটা ব্যবধানে রাখলে পারস্পরিক বিকর্ষণ বল সর্বাধিক হবে।
আধানের কোয়ান্টিভবন কাকে বলে?
কোনো আহিত বস্তুর মোট আধান সর্বদা ইলেকট্রনের আধানের পূর্ণ গুণিতক হয়, এই ঘটনাকে আধানের কোয়ান্টিভবন বলা হয়।
আধানের সংরক্ষণ কাকে বলে?
কোনো বিচ্ছিন্ন বস্তু সংস্থার মোট আধান সর্বদা ধ্রুবক থাকে অর্থাৎ আধানের সৃষ্টি বা ধ্বংস হয় না। আধান শুধুমাত্র কোনো বস্তু সংস্থার এক অংশ থেকে অন্য অংশে স্থানান্তরিত হয়।
সমভরের দুটি বস্তু A ও B। A ও B -কে যথাক্রমে সমপরিমাণ ধনাত্মক ও ঋণাত্মক আধানে আহিত করা হল। আহিত করার পর তাদের ভরের কীরূপ পরিবর্তন হবে?
মনে করি, \( A \) বস্তুর আধান \( q \) ও \( B \) বস্তুর আধান \( -q \)। একটি ইলেকট্রনের আধানের মান \( e \) হলে \( A \) বস্তুটি \( \frac qe \) সংখ্যক ইলেকট্রন বর্জন করে ও \( B \) বস্তুটি \( \frac qe \) সংখ্যক ইলেকট্রন গ্রহণ করে। একটি ইলেকট্রনের ভর \( m \) হলে \( A \) বস্তুর ভর \( \frac{qm}e \) পরিমাণ হ্রাস পাবে এবং B বস্তুর ভর \( \frac{qm}e \) পরিমাণ বৃদ্ধি পাবে।
সাধারণ রবার তড়িতের কুপরিবাহী কিন্তু এরোপ্লেনের টায়ার কিছুটা তড়িৎ পরিবাহী করা হয় কেন?
এরোপ্লেন ওঠার বা নামার সময় রানওয়ে দিয়ে তীব্র বেগে এগিয়ে যায়। ফলে রাস্তা ও টায়ারের ঘর্ষণের ফলে টায়ার তড়িদাহিত হয়। এইজন্য দুর্ঘটনা ঘটার সম্ভবনা থাকে। টায়ার সামান্য তড়িৎ পরিবাহী করায় ঘর্ষণে উৎপন্ন আধান ভূমিতে চলে যায় ফলে দুর্ঘটনার সম্ভাবনা কমে যায়।
তড়িৎবিভব, বিভবপ্রভেদ, তড়িৎকোশ ও তড়িৎপ্রবাহমাত্রা
তড়িৎক্ষেত্র কাকে বলে?
একটি আধানকে কোনো স্থানে রাখলে সেই আধানটি তার চারপাশে এমন একটি ক্ষেত্র বা অঞ্চল তৈরি করে যেখানে অন্য কোনো আধান রাখলে সেই আধানটি একটি তড়িৎ বল অনুভব করে। এই অঞ্চলকে তড়িৎক্ষেত্র বলে।
তড়িৎবিভব কাকে বলে?
অসীম দূরত্ব থেকে একটি একক ধনাত্মক তড়িদাধানকে তড়িৎক্ষেত্রের কোনো বিন্দুতে আনতে যে কার্য করতে হয় তাকে তড়িৎক্ষেত্রের ওই বিন্দুতে তড়িৎবিভব বলা হয়।
CGS পদ্ধতি ও SI -তে তড়িৎবিভবের এককগুলি কী কী? এদের সংজ্ঞা লেখো।
CGS পদ্ধতি ও SI -তে তড়িৎবিভবের একক যথাক্রমে esu বিভব বা স্ট্যাটভোল্ট (statvolt) এবং ভোল্ট (V)।
esu বিভব বা স্ট্যাটডোল্ট – অসীম দূরত্ব থেকে 1 esu ধনাত্মক আধানকে তড়িৎক্ষেত্রের কোনো বিন্দুতে আনতে যদি 1 erg কার্য সম্পাদন করতে হয় তবে ওই বিন্দুর তড়িৎবিভবকে 1 esu বিভব বা 1 স্ট্যাটভোল্ট বলে।
ভোল্ট – অসীম দূরত্ব থেকে 1 C ধনাত্মক আধানকে তড়িৎক্ষেত্রের কোনো বিন্দুতে আনতে যদি 1 J কার্য সম্পাদন করতে হয় তবে ওই বিন্দুর তড়িৎবিভবকে 1 V (ভোল্ট) বলে।
esu বিভব ও ভোল্ট (V) -এর মধ্যে সম্পর্ক স্থাপন করো।
তড়িৎক্ষেত্রের কোনো বিন্দুতে তড়িৎবিভব \( V \) হলে অসীম দূরত্ব থেকে \( q \) আধানকে ওই বিন্দুতে আনতে কৃত কার্য,
\( W=qV \\\)বা, \( V=\frac Wq \)
∴ \( 1V=\frac{1J}{1C} \)
=
= \( \frac1{300}\;esu \) বিভব
বা, 1 esu বিভব = 300 V
একক ধনাত্মক আধানের সরণে কৃত কার্য রূপে বিভবপ্রভেদের ধারণা দাও। এর থেকে বিভবপ্রভেদের CGS ও SI এককের সংজ্ঞা দাও।
মনে করি, তড়িৎক্ষেত্রে অবস্থিত \( R \) ও \( S \) বিন্দুতে তড়িৎবিভব যথাক্রমে \( V_R \) ও \( V_S \), অর্থাৎ একক ধনাত্মক আধানকে অসীম দূরত্ব থেকে \( R \) বিন্দুতে আনতে কৃত কার্য \( V_R \) ও \( S \) বিন্দুতে আনতে কৃত কার্য \( V_S \)। সুতরাং একক ধনাত্মক আধানটিকে \( R \) থেকে \( S \) বিন্দুতে আনতে কৃত কার্য \( =V_S-V_R \)। এটিই হল \( S \) ও \( R \) বিন্দু দুটির মধ্যে বিভবপ্রভেদ ।
\( S \) ও \( R \) বিন্দু দুটির মধ্যে বিভবপ্রভেদ \( V_{SR} \) হলে, \( V_{SR}=V_S-V_R \)।
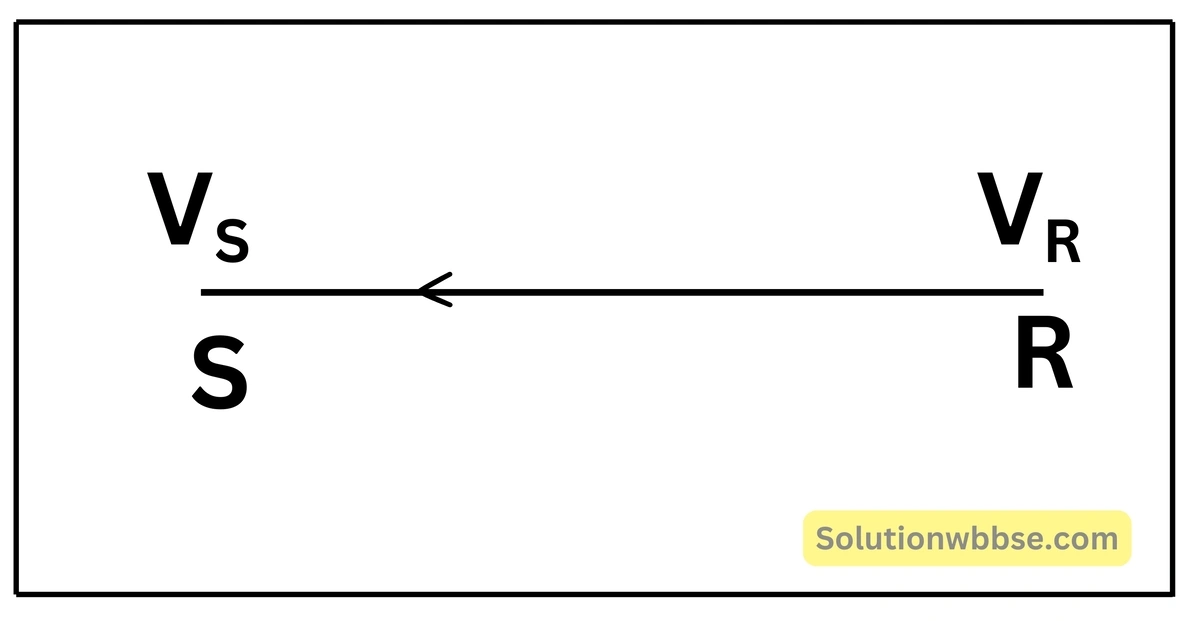
যদি \( q \) আধানকে \( R \) থেকে \( S \) বিন্দুতে আনা হয় তাহলে কৃত কার্য \( W=q\cdot V_{SR} \)
বা, \( V_{SR}=\frac Wq \) ___(1)
\( CGS \) পদ্ধতি ও \( SI \) -তে বিভবপ্রভেদের একক যথাক্রমে \( esu \) বিভব ও \( V \) (ভোল্ট)।
\( q=1\;esu,\;W=1\;erg \) হলে \( V_{SR}=1\;esu \) বিভব হবে অর্থাৎ তড়িৎক্ষেত্রে অবস্থিত একটি বিন্দু থেকে অপর একটি বিন্দুতে \( 1\;esu \) ধনাত্মক আধানকে নিয়ে যেতে যদি \( 1\;erg \) কার্য করতে হয় তবে ওই দুই বিন্দুর বিভবপ্রভেদকে \( 1\;esu \) বিভব বা \( 1 \) স্ট্যাটভোল্ট বলা হয়।
আবার, \( q=1\;C,\;W=1\;J \) হলে \( V_{SR}=1\;V \) হবে অর্থাৎ তড়িৎক্ষেত্রে অবস্থিত একটি বিন্দু থেকে অপর একটি বিন্দুতে \( 1\;C \) ধনাত্মক আধানকে নিয়ে যেতে যদি \( 1\;J \) কার্য করতে হয় তাহলে ওই দুই বিন্দুর বিভবপ্রভেদকে \( 1\;V \) (ভোল্ট) বলা হয়।
তড়িৎকোশ কাকে বলে? তড়িৎকোশকে কীভাবে প্রকাশ করা হয়?
তড়িৎকোশ হল এমন একটি ব্যবস্থা যেখানে কোনো যন্ত্রের সাহায্য ছাড়া অন্য কোনো শক্তিকে তড়িৎশক্তিতে রূপান্তরিত করা যায়।
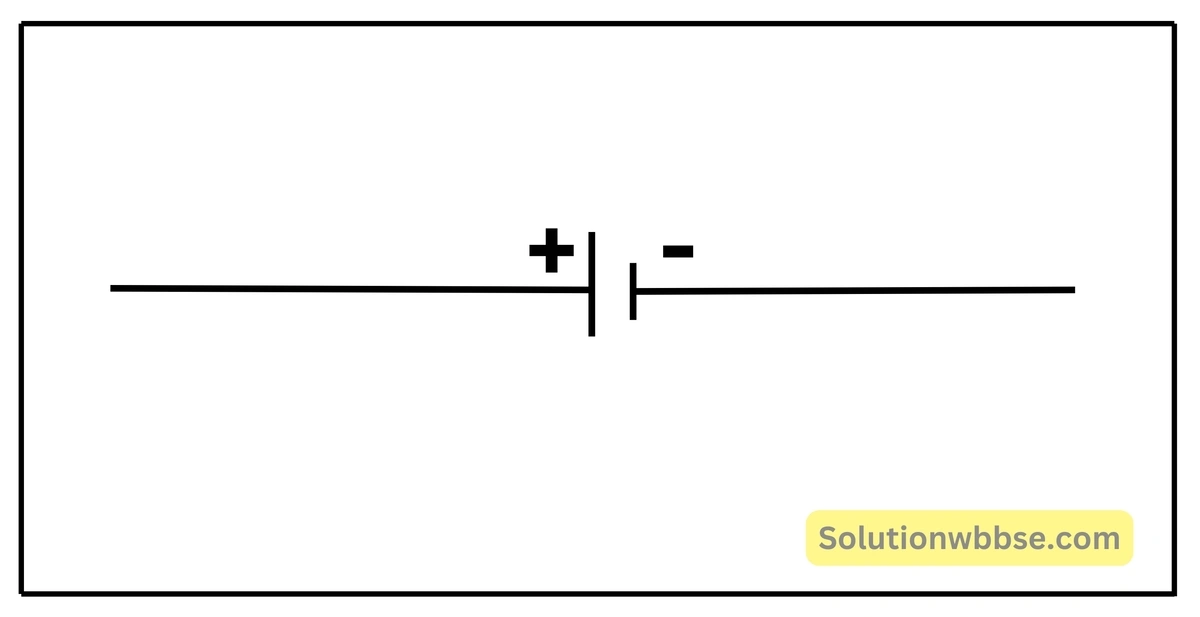
পাশাপাশি দুটি অসমান সমান্তরাল রেখাংশ দ্বারা একটি তড়িৎকোশকে প্রকাশ করা হয়। বড়ো রেখাংশটি তড়িৎকোশের ধনাত্মক মেরু ও ছোটো রেখাংশটি কোশের ঋণাত্মক মেরুকে প্রকাশ করে।
কৃত কার্যের ধারণা থেকে তড়িৎকোশের EMF -এর সংজ্ঞা দাও।
একক ধনাত্মক তড়িদাধানকে তড়িৎকোশসহ কোনো সংহত তড়িৎবর্তনী বরাবর একবার ঘুরিয়ে আনতে যে কার্য সম্পাদন করতে হয় তা হল ওই তড়িৎকোশের EMF।
SI -তে EMF -এর এককের সংজ্ঞা লেখো।
SI -তে EMF -এর একক V (ভোল্ট)।
1 C ধনাত্মক তড়িদাধানকে তড়িৎকোশসহ কোনো সংহত তড়িৎবর্তনী বরাবর একবার ঘুরিয়ে আনতে যদি 1 J কার্য সম্পাদন করতে হয় তাহলে ওই তড়িৎকোশের EMF হল 1 V।
হ্রস্ব বর্তনী বা শর্ট সার্কিট বলতে কী বোঝ?
কোনো তড়িৎ উৎসের দুটি মেরুকে প্রায় রোধহীন বা নগণ্য রোধের কোনো পরিবাহী তার দিয়ে যুক্ত করা হলে, সেই বর্তনীকে হ্রস্ব বর্তনী বা শর্ট সার্কিট বলা হয়।
রোধ অত্যন্ত কম হওয়ায় তড়িৎপ্রবাহ বেশি হয়, তাই তারটি খুবই উত্তপ্ত হয়। এতে তড়িৎ বর্তনীর ক্ষতি হতে পারে।
কোনো তড়িৎকোশের EMF 10 V – বলতে কী বোঝ?
কোনো তড়িৎকোশের EMF 10 V বলতে বোঝায়, 1 C তড়িদাধানকে তড়িৎকোশসহ কোনো সংহত তড়িৎবর্তনী বরাবর একবার ঘুরিয়ে আনতে 10 J কার্য সম্পাদন করতে হয়।
মুক্ত বর্তনীতে কোশের তড়িৎচালক বলের সংজ্ঞা দাও।
মুক্ত বর্তনীতে কোনো কোশের অভ্যন্তরে একক ধনাত্মক তড়িদাধানকে কোশের ঋণাত্মক মেরু থেকে ধনাত্মক মেরুতে নিয়ে যেতে বাহ্যিক সংস্থা দ্বারা কৃত কার্য-ই হল কোশের তড়িৎচালক বল।
তড়িৎপ্রবাহ কাকে বলে?
কোনো পরিবাহীর মধ্যে দিয়ে তড়িদ্গ্রস্ত কণার প্রবাহকে তড়িৎপ্রবাহ বলে। পরিবাহীর যে-কোনো প্রস্থচ্ছেদের মধ্য দিয়ে যে পরিমাণ তড়িদ্গ্রস্ত কণা প্রবাহিত হয় তা হল তড়িৎপ্রবাহের পরিমাণ।
তড়িৎপ্রবাহ ও আধানের মধ্যে সম্পর্ক স্থাপন করো।
পরিবাহীর কোনো প্রস্থচ্ছেদের মধ্য দিয়ে \( t \) সময়ে \( q \) আধান প্রবাহিত হলে একক সময়ে প্রবাহিত আধান \( =\frac qt \)।
∴ তড়িৎপ্রবাহ, \( I=\frac qt \)।
SI -তে তড়িৎপ্রবাহের এককের সংজ্ঞা দাও।
তড়িৎপ্রবাহের SI একক হল A (অ্যাম্পিয়ার)।
পরিবাহীর কোনো প্রস্থচ্ছেদের মধ্য দিয়ে 1 s সময়ে 1 C আধান প্রবাহিত হলে ওই তড়িৎপ্রবাহকে 1 A বলা হয়।
ধাতব পরিবাহীর মধ্যে কীভাবে তড়িৎপ্রবাহ হয়? তড়িৎপ্রবাহের অভিমুখ কী?
ধাতব পরিবাহীর মধ্যে মুক্ত ইলেকট্রনগুলি হল তড়িতের বাহক। পরিবাহীর দু-প্রান্তে বিভবপ্রভেদ প্রয়োগ করলে মুক্ত ইলেকট্রনগুলি নিম্নবিভব থেকে উচ্চবিভবের দিকে গতিশীল হয় ফলে পরিবাহীর মধ্য দিয়ে তড়িৎপ্রবাহ হচ্ছে বলা হয়।
তড়িৎপ্রবাহের অভিমুখ বলতে ধনাত্মক আধানের গতির অভিমুখকে বোঝায়। ধাতব পরিবাহীর ক্ষেত্রে তড়িৎপ্রবাহের অভিমুখ হল মুক্ত ইলেকট্রনের গতির বিপরীত অভিমুখে।
তড়িৎপ্রবাহের অভিমুখ থাকা সত্ত্বেও এটি স্কেলার রাশি কেন?
তড়িৎপ্রবাহের মান ও অভিমুখ আছে কিন্তু তড়িৎপ্রবাহ স্কেলার রাশি কারণ তড়িৎপ্রবাহের যোগ ভেক্টর যোগের নিয়মানুযায়ী হয় না।
ওহমের সূত্র
ওহমের সূত্রটি লেখো।
ওহমের সূত্র – পরিবাহীর তাপমাত্রা ও অন্যান্য ভৌত অবস্থা অপরিবর্তিত থাকলে পরিবাহীর মধ্য দিয়ে প্রবাহমাত্রা পরিবাহীর দুই প্রান্তের বিভবপ্রভেদের সমানুপাতিক।
ওহমের সূত্রটি ব্যাখ্যা করো এবং রোধের ধারণা দাও।
মনে করি, কোনো পরিবাহীর দু-প্রান্ত \( A \) ও \( B \) -এর তড়িৎবিভব যথাক্রমে \( V_A \) ও \( V_B \) । \( V_A>V_B \) হলে \( A \) থেকে \( B \) -এর দিকে তড়িৎপ্রবাহ হবে। তড়িৎপ্রবাহ \( I \) হলে, ওহমের সূত্রানুযায়ী,
\( I\propto\left(V_A-V_B\right) \\\)বা, \( \frac{V_A-V_B}I=K \)
বা, \( V_A-V_B=KI \), যেখানে \( K \) একটি ধ্রুবক।
বিভবপ্রভেদ, \( V_A-V_B=V \) হলে, \( V=KI \) ___(1)
কয়েকটি ভিন্ন পদার্থের কিন্তু জ্যামিতিকভাবে অভিন্ন পরিবাহীর দু-প্রান্তের বিভবপ্রভেদ \( V \) স্থির রাখলে দেখা যায় বিভিন্ন ক্ষেত্রে তড়িৎপ্রবাহ \( I \) বিভিন্ন হয়। অর্থাৎ যে পরিবাহীতে প্রবাহমাত্রা \( I \) -এর মান কম তার \( K \) -এর মান বেশি। আবার যে পরিবাহীতে প্রবাহমাত্রা \( I \) -এর মান বেশি তার \( K \) -এর মান কম। সুতরাং, \( K \) শুধুমাত্র একটি ধ্রুবক নয়, এটি জ্যামিতিকভাবে অভিন্ন এবং বিভিন্ন পরিবাহীর ক্ষেত্রে বিভিন্ন। অর্থাৎ \( K \) রাশিটি এমন কিছু নির্দেশ করে যাতে পরিবাহীর মধ্য দিয়ে প্রবাহমাত্রা বাধাপ্রাপ্ত হয়, তাই \( K \) -কে পরিবাহীর রোধ বলা হয় এবং একে \( R \) দ্বারা প্রকাশ করা হয়। সুতরাং, যে ধর্মের জন্য কোনো পরিবাহী ওর মধ্য দিয়ে তড়িৎপ্রবাহকে বাধা দেয়, তাকে পরিবাহীর রোধ বলে।
∴ ওহমের সূত্রের সমীকরণটি হল, \( V=IR \)।
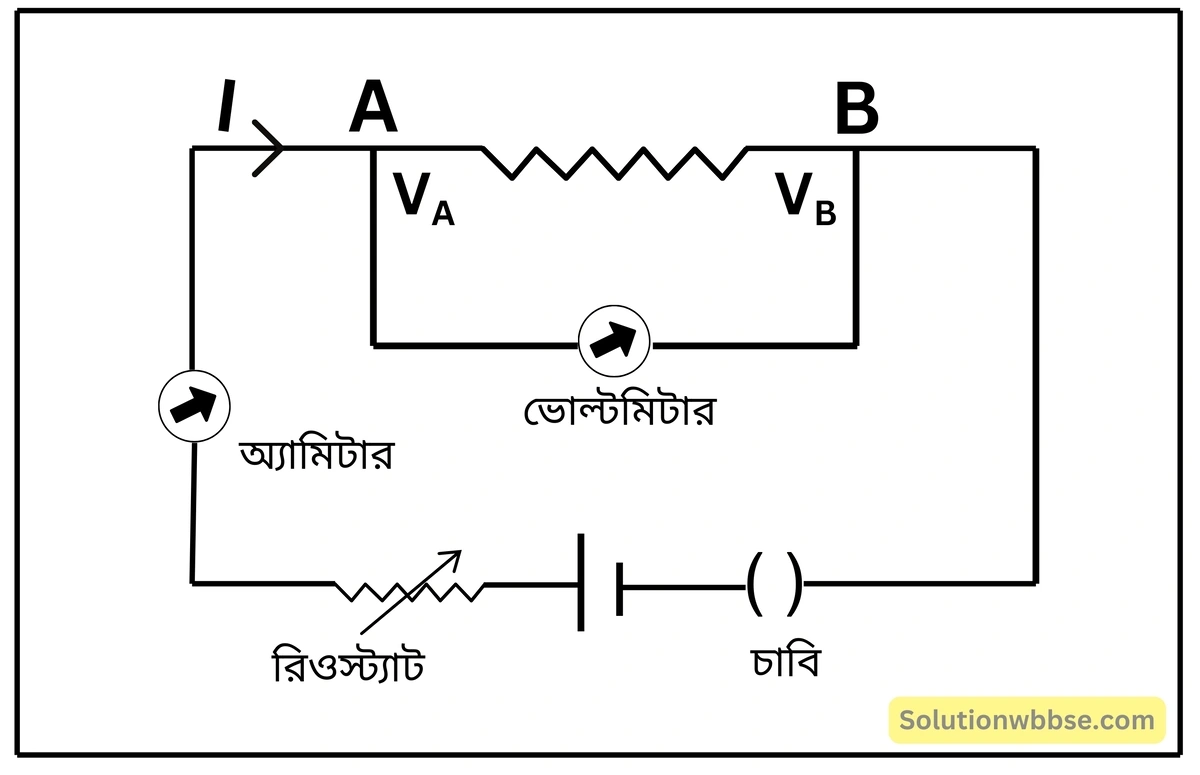
ওহমের সূত্র থেকে রোধের সংজ্ঞা দাও।
কোনো পরিবাহীর দু-প্রান্তে বিভব পার্থক্য সৃষ্টি করলে পরিবাহীর মধ্য দিয়ে তড়িৎ প্রবাহ হয়। পরিবাহীর দু-প্রান্তের বিভবপ্রভেদ ও পরিবাহীর মধ্য দিয়ে তড়িৎপ্রবাহের অনুপাতকে পরিবাহীর রোধ বলা হয়।
SI -তে রোধের এককের সংজ্ঞা দাও।
\( SI \) -তে রোধের একক ওহম (ohm বা Ω)। \( 1\;\Omega\;=1\frac VA \)। কোনো পরিবাহীর দু-প্রান্তে \( 1\;V \) বিভবপ্রভেদ প্রয়োগ করলে যদি পরিবাহীর মধ্য দিয়ে \( 1\;A \) তড়িৎপ্রবাহ হয় তাহলে পরিবাহীর রোধকে \( 1\;\Omega \) বলা হয়।
আন্তর্জাতিক অ্যাম্পিয়ার কাকে বলে?
শূন্যস্থানে \( 1\;m \) ব্যবধানে রক্ষিত দুটি অসীম দীর্ঘ, নগণ্য প্রস্থচ্ছেদের ক্ষেত্রফলযুক্ত ঋজু পরিবাহী তারের প্রতিটির মধ্য দিয়ে যে মানের তড়িৎপ্রবাহ হলে তার দুটির প্রতি মিটার দৈর্ঘ্যে \( 2\times10^{-7}\;N \) বল ক্রিয়াশীল হয় তাকে \( 1\;A \) বলা হয়।
আন্তর্জাতিক ভোল্ট কাকে বলে?
20°C উষ্ণতায় একটি ওয়েস্টন-ক্যাডমিয়াম কোশের তড়িৎচালক বলের \( \frac1{1.0183} \) অংশকে \( 1\;V\;\left(volt\right) \) বলা হয়।
আন্তর্জাতিক ওহম কাকে বলে?
0°C উষ্ণতায় রক্ষিত সুষম প্রস্থচ্ছেদবিশিষ্ট 14.4521 g ভর ও 106.3 cm দীর্ঘ পারদস্তম্ভের রোধকে 1 Ω বলা হয়।
লেখচিত্রের সাহায্যে ওহমের সূত্রকে প্রকাশ করো।
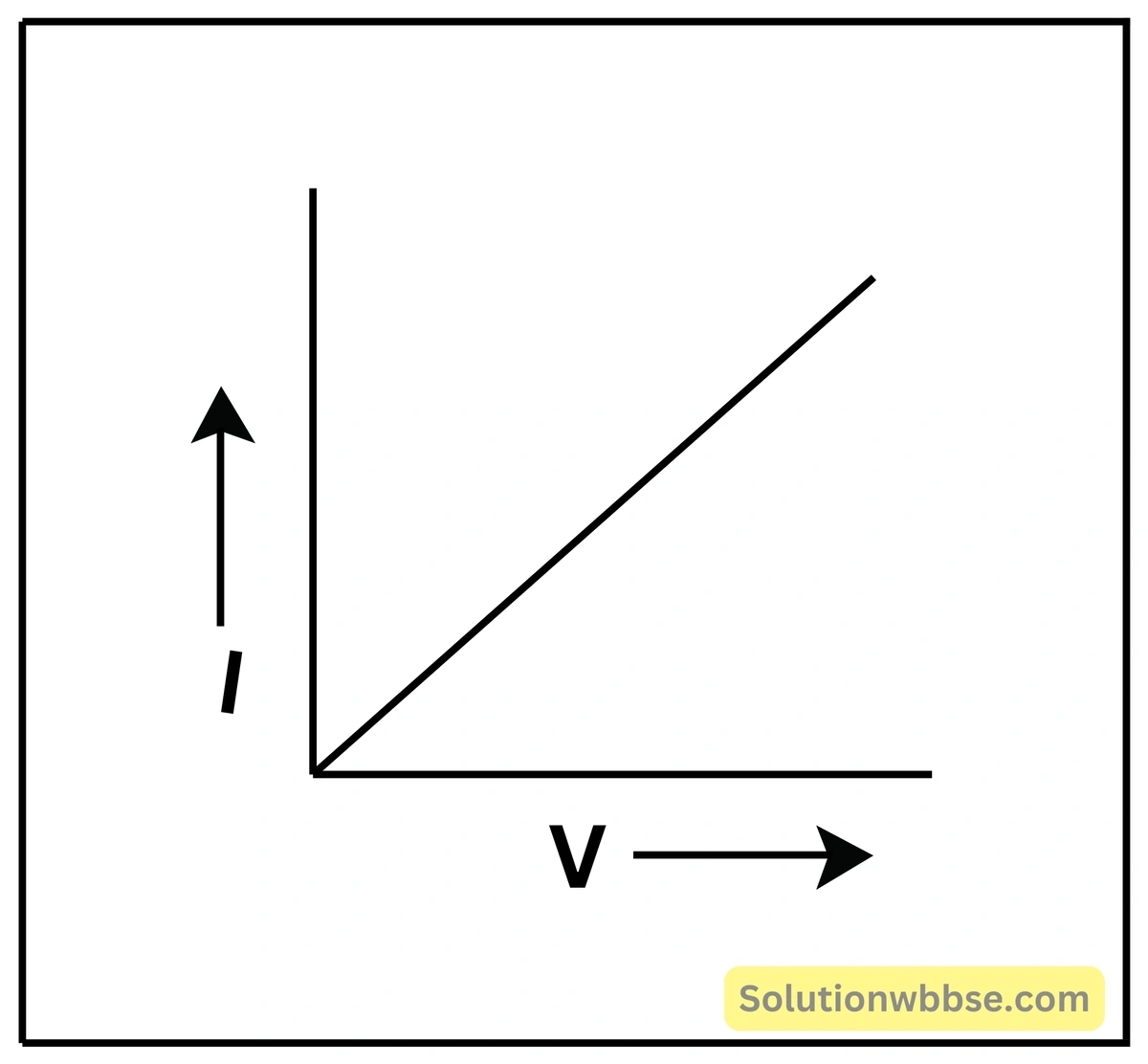
কোনো পরিবাহীর দু-প্রান্তের বিভবপ্রভেদ পরিবর্তন করলে পরিবাহীর মধ্য দিয়ে তড়িৎপ্রবাহের পরিবর্তন হয়। পরিবাহীর দু-প্রান্তের বিভবপ্রভেদ \( V \) ও তড়িৎপ্রবাহ \( I \) হলে, ওহমের সূত্রানুযায়ী, \( V=IR \)। বিভবপ্রভেদ \( V \) -কে ভুজ ও ওই সময় পরিবাহীর মধ্য দিয়ে তড়িৎপ্রবাহ \( I \) -কে কোটি ধরে লেখচিত্র অঙ্কন করলে যে লেখচিত্র পাওয়া যায় তাকে পরিবাহীর \( I-V \) লেখচিত্র বলা হয়। লেখচিত্রটি মূল বিন্দুগামী সরলরেখা। এটিই হল লেখচিত্রের সাহায্যে ওহমের সূত্রের প্রকাশ।
ওহমীয় পরিবাহী ও অ-ওহমীয় পরিবাহী কাকে বলে? উদাহরণ দাও।
ওহমীয় পরিবাহী – যে সমস্ত পরিবাহী ওহমের সূত্র মেনে চলে বা যে সমস্ত পরিবাহীর \( I-V \) লেখচিত্র মূলবিন্দুগামী সরলরেখা, তাদের ওহমীয় পরিবাহী বলা হয়। যেমন – সমস্ত ধাতব পরিবাহী।
অ-ওহমীয় পরিবাহী – যে সমস্ত পরিবাহী ওহমের সূত্র মেনে চলে না বা যে সমস্ত পরিবাহীর \( I-V \) লেখচিত্র মূলবিন্দুগামী সরলরেখা হয় না, তাদের অ-ওহমীয় পরিবাহী বলা হয়। যেমন – ডায়োড, ট্রায়োড, ট্রানজিস্টার।
পরিবাহীর রোধ কী কী বিষয়ের ওপর নির্ভরশীল?
কোনো পরিবাহীর রোধ সাধারণত নিম্নলিখিত বিষয়গুলির ওপর নির্ভরশীল –
- পরিবাহীর দৈর্ঘ্য
- প্রস্থচ্ছেদের ক্ষেত্রফল
- পরিবাহীর উপাদান
- পরিবাহীর তাপমাত্রা
এ ছাড়া কোনো কোনো পরিবাহীর রোধ –
- আলোর তীব্রতা
- চৌম্বক ক্ষেত্র প্রাবল্য
- চাপের ওপরও নির্ভরশীল।
নির্দিষ্ট তাপমাত্রায় কোনো পরিবাহীর রোধ কী কী বিষয়ের ওপর ও কীভাবে নির্ভর করে?
নির্দিষ্ট তাপমাত্রায় কোনো পরিবাহীর রোধ \( \left(R\right) \) পরিবাহীর দৈর্ঘ্য \( \left(l\right) \), প্রস্থচ্ছেদের ক্ষেত্রফল \( \left(A\right) \) ও উপাদানের ওপর নির্ভরশীল।
কোনো পরিবাহীর প্রস্থচ্ছেদের ক্ষেত্রফল অপরিবর্তিত থাকলে পরিবাহীর রোধ তার দৈর্ঘ্যের সমানুপাতিক।
অর্থাৎ \( R\propto l \) [যখন A স্থির] ___(1)
আবার, পরিবাহীর দৈর্ঘ্য অপরিবর্তিত থাকলে পরিবাহীর রোধ তার প্রস্থচ্ছেদের ক্ষেত্রফলের ব্যস্তানুপাতিক।
অর্থাৎ \( R\propto\frac 1 A \) [যখন \( l \) স্থির] ___(2)
(1) ও (2) নং সমীকরণ থেকে যৌগিক ভেদের নিয়মানুযায়ী পাই,
\( R\propto\frac lA \) [যখন \( l \) ও \( A \) উভয়ই পরিবর্তনশীল]
বা, \( R=\rho\frac lA \)
যেখানে \( \rho \) একটি ধ্রুবক; \( \rho \) -কে পরিবাহীর উপাদানের রোধাঙ্ক বলা হয়। এর মান পরিবাহীর উপাদান ও অন্যান্য ভৌত অবস্থার ওপর নির্ভর করে।
রোধাঙ্ক কাকে বলে?
একক দৈর্ঘ্য ও একক প্রস্থচ্ছেদের ক্ষেত্রফলবিশিষ্ট কোনো পরিবাহীর দুই বিপরীত পৃষ্ঠের রোধকে ওই পরিবাহীর উপাদানের রোধাঙ্ক বলা হয়।
তামার রোধাঙ্ক \( 1.68\times10^{-6}\;\Omega\cdot cm \) (20°C উষ্ণতায়) বলতে কী বোঝ?
তামার রোধাঙ্ক \( 1.68\times10^{-6}\;\Omega\cdot cm \) (20°C উষ্ণতায়) বলতে বোঝায় 20°C উষ্ণতায় \( 1\;cm \) দৈর্ঘ্য ও \( 1\;cm^2 \) প্রস্থচ্ছেদের ক্ষেত্রফলবিশিষ্ট তামার ব্লকের দুই বিপরীত পৃষ্ঠের রোধ \( 1.68\times10^{-6}\;\Omega \)।
SI -তে রোধাঙ্কের একক নির্ণয় করো।
\( l \) দৈর্ঘ্য, \( A \) প্রস্থচ্ছেদের ক্ষেত্রফলবিশিষ্ট কোনো পরিবাহীর উপাদানের রোধাঙ্ক \( \rho \) হলে, রোধ, \( R=\rho\cdot\frac lA \)
বা, \( \rho=\frac{RA}l \)
∴ SI -তে রোধাঙ্কের একক =
বা, \( SI \) -তে রোধাঙ্কের একক = \( \frac{\Omega\times m^2}m=\Omega\cdot m \)
পরিবাহীর রোধের ওপর চাপের প্রভাব কী?
বেশিরভাগ ধাতুর ওপর চাপ প্রয়োগ করলে রোধ কমে যায়। তবে \( Li,\;Ca,\;Bi \) -এর ওপর চাপ প্রয়োগ করলে রোধ কমার পরিবর্তে বৃদ্ধি পায়। কার্বনের ওপর চাপ প্রয়োগ করলে রোধ কমে।
পরিবাহীর রোধের ওপর আলোর প্রভাব কী?
কিছু পরিবাহীর রোধ আপতিত আলোর তীব্রতার ওপর নির্ভরশীল। সেলেনিয়াম ধাতুর ওপর আলো ফেললে রোধ কমে যায়। আলোর তীব্রতা বাড়ালে রোধ আরও কমে যায়।
কতকগুলি পদার্থের রোধাঙ্ক
| পদার্থ | রোধাঙ্ক \( \left(\Omega\cdot m\right) \) [20°C উষ্ণতায়] |
| রুপো | 1.59 × 10-8 |
| তামা | 1.68 × 10-8 |
| সোনা | 2.44 × 10-8 |
| টাংস্টেন | 5.6 × 10-8 |
| জিংক | 5.9 × 10-8 |
| নিকেল | 6.99 × 10-8 |
| লোহা | 10.0 × 10-8 |
| টিন | 10.9 × 10-8 |
| কনস্ট্যানটান | 49 × 10-8 |
পরিবাহিতা ও পরিবাহিতাঙ্ক কাকে বলে? এদের রাশিমালা ও SI একক লেখো।
পরিবাহিতা – পরিবাহী যে ধর্মের জন্য ওর মধ্য দিয়ে তড়িৎপ্রবাহ যেতে সাহায্য করে, তাকে পরিবাহীর পরিবাহিতা বলা হয়। কোনো পরিবাহীর রোধ \( R \) হলে, পরিবাহিতা, \( k=\frac1R \) ।
পরিবাহিতার একক হল mho (℧), \( SI \) -তে \( mho \) -এর অন্য নাম সিমেন্স \( \left(S\right) \)।
পরিবাহিতাঙ্ক – একক দৈর্ঘ্য ও একক প্রস্থচ্ছেদের ক্ষেত্রফলযুক্ত কোনো পরিবাহীর পরিবাহিতাকে ওই পরিবাহীর উপাদানের পরিবাহিতাঙ্ক বলা হয়।
কোনো পরিবাহীর উপাদানের রোধাঙ্ক \( \rho \) হলে পরিবাহিতাঙ্ক \( \sigma=\frac1\rho \)।
\( SI \) -তে পরিবাহিতাঙ্কের একক \( mho\cdot m^{-1}\)(℧⋅m-1) তবে এটি \( S\cdot m^{-1} \) এককেও ব্যবহৃত হয়।
পরিবাহীর রোধের মাত্রীয় সংকেত নির্ণয় করো।
কোনো পরিবাহীর দুই প্রান্তে \( V \) বিভবপ্রভেদ প্রয়োগ করলে যদি \( I \) তড়িৎপ্রবাহ হয় তাহলে পরিবাহীর রোধ, \( R=\frac VI \)
রোধ =
রোধ =
রোধ =
∴ রোধের মাত্রীয় সংকেত \( =\frac{ML^2T^{-2}}{I^2\times T}=ML^2T^{-3}I^{-2} \)
কোনো পরিবাহীর দৈর্ঘ্য বাড়লে পরিবাহীর রোধ বাড়ে কিন্তু প্রস্থচ্ছেদের ক্ষেত্রফল বাড়লে রোধ কমে কেন?
কোনো পরিবাহীর প্রস্থচ্ছেদের ক্ষেত্রফল অপরিবর্তিত অবস্থায় দৈর্ঘ্য বেশি হলে পরিবাহীর মধ্যে তড়িতের বাহক মুক্ত ইলেকট্রনগুলি আরও বেশি সংখ্যক ধাক্কার সম্মুখীন হয়, তাই বাধা বা রোধ বাড়ে। আবার দৈর্ঘ্য অপরিবর্তিত অবস্থায় প্রস্থচ্ছেদের ক্ষেত্রফল বেশি হলে পরিবাহীর মধ্যে তড়িতের বাহক মুক্ত ইলেকট্রনগুলি যাতায়াতের জন্য বেশি জায়গা পায়, তাই কম সংখ্যক ধাক্কার সম্মুখীন হয় ফলে বাধা বা রোধ কমে।
দেখাও কোনো ওহমীয় পরিবাহীর \( I-V \) লেখচিত্র বিভবপ্রভেদ অক্ষের সঙ্গে \( \theta \) কোণ করলে পরিবাহীর রোধ, \( R=cot\theta \)
নীচের চিত্রে একটি ওহমীয় পরিবাহীর \( I-V \) লেখচিত্র \( \left(OA\right) \) দেখানো হয়েছে। লেখচিত্রটি মূলবিন্দুগামী সরলরেখা। \( OA \) সরলরেখার ওপর একটি বিন্দু \( C \) নেওয়া হল। \( C \) থেকে বিভবপ্রভেদ অক্ষের ওপর \( CB \) লম্ব টানা হল। অর্থাৎ পরিবাহীর দু-প্রান্তে \( OB=V \) বিভবপ্রভেদ প্রয়োগ করা হলে তড়িৎপ্রবাহ হয় \( BC=I \)
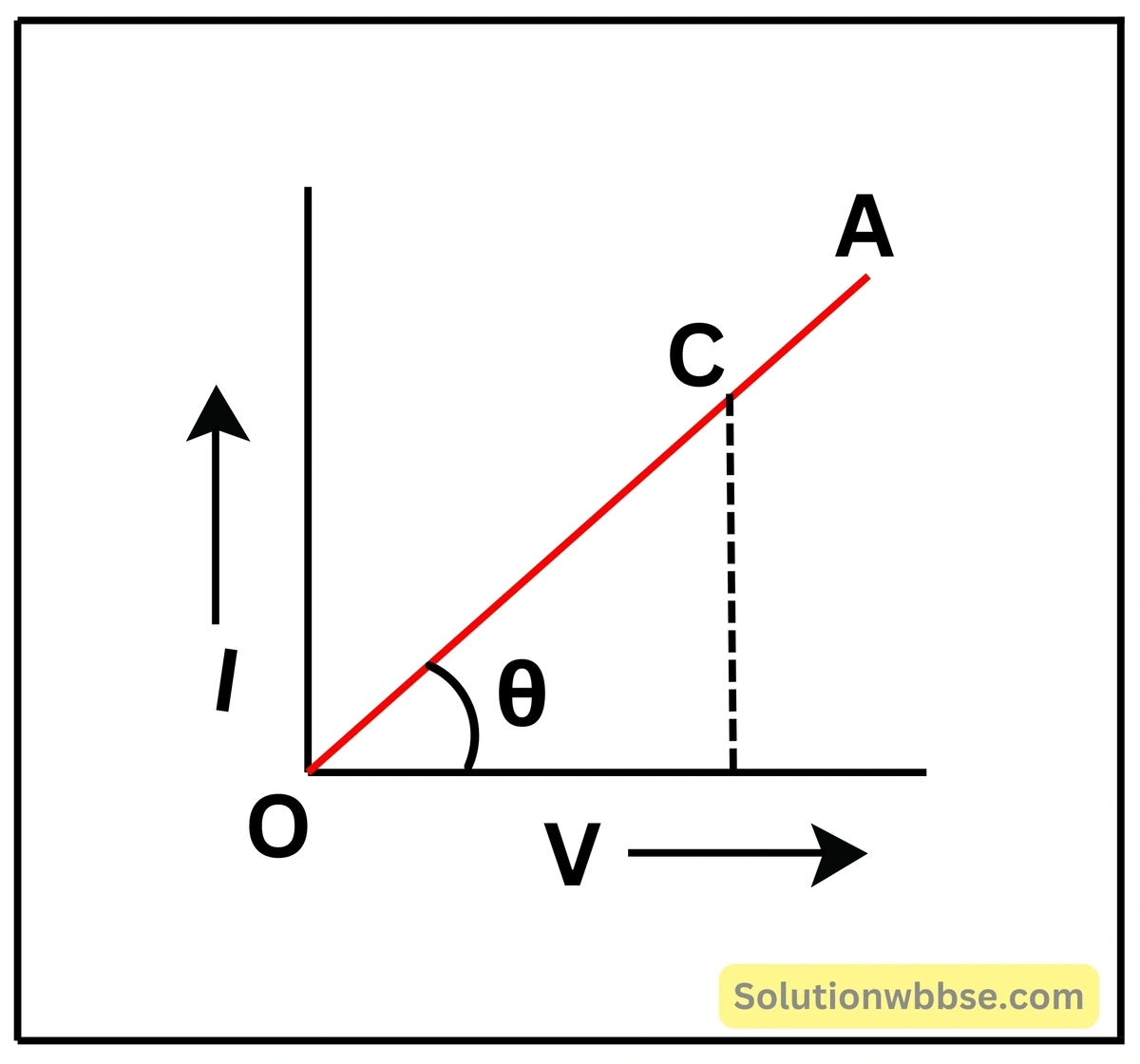
∴ পরিবাহীর রোধ, \( R=\frac VI=\frac{OB}{BC}=cot\theta \)
∴ \( R=cot\theta \) [প্রমাণিত]
তড়িতের সুপরিবাহী, অন্তরক ও অর্ধপরিবাহী কাকে বলে? প্রতিটির রোধাঙ্কের মান কত?
সুপরিবাহী – যেসব পদার্থ সহজে তড়িৎ পরিবহণ করতে পারে তাদের সুপরিবাহী বলা হয়। যেমন – ধাতব পরিবাহী।
সুপরিবাহীর রোধাঙ্কের মান প্রায় \( 10^{-8}\;\Omega\cdot m \) থেকে \( 10^{-6}\;\Omega\cdot m \) -এর মধ্যে হয়।
অন্তরক – যেসব পদার্থ সাধারণত তড়িৎ পরিবহণ করতে পারে না তাদের অন্তরক বলা হয়। যেমন – কাচ, প্লাস্টিক, রবার।
অন্তরকের রোধাঙ্কের মান প্রায় \( 10^{10}\;\Omega\cdot m \) থেকে \( 10^{17}\;\Omega\cdot m \) -এর মধ্যে হয়।
অর্ধপরিবাহী – যেসব পদার্থের তড়িৎ পরিবাহিতা সুপরিবাহীর তুলনায় কম কিন্তু অন্তরকের তুলনায় বেশি তাদের অর্ধপরিবাহী বলা হয়। যেমন – জার্মেনিয়াম, সিলিকন।
অর্ধপরিবাহীর রোধাঙ্কের মান প্রায় \( 10^{-5}\;\Omega\cdot m \) থেকে \( 10^{-2}\;\Omega\cdot m \) -এর মধ্যে হয়।
দৈনন্দিন জীবনে অন্তরকের ব্যবহার সংক্ষেপে লেখো।
কোনো পরিবাহীর মধ্য দিয়ে তড়িৎপ্রবাহ হলে তা যদি স্পর্শ করা হয় তাহলে শক লাগে, কারণ আমাদের শরীর তড়িতের সুপরিবাহী। তড়িতের শক লাগা খুবই বিপজ্জনক। এর থেকে রক্ষা করে অন্তরক পদার্থ। তাই পরিবাহী তারে সর্বদা অন্তরক পদার্থ যেমন পলিইথিলিন -এর আবরণ দেওয়া হয়। ট্রেনের ওভারহেড তারে সেরামিক অন্তরক ব্যবহার করা হয়। আবার তড়িতের কাজে লাগে এমন অনেক তড়িৎযন্ত্র যেমন প্লায়ার্স, টেস্টার -এর হাতল অন্তরক পদার্থের তৈরি হয়।

কোনো অর্ধপরিবাহীর রোধাঙ্ক-উষ্ণতা লেখচিত্র আঁকো।
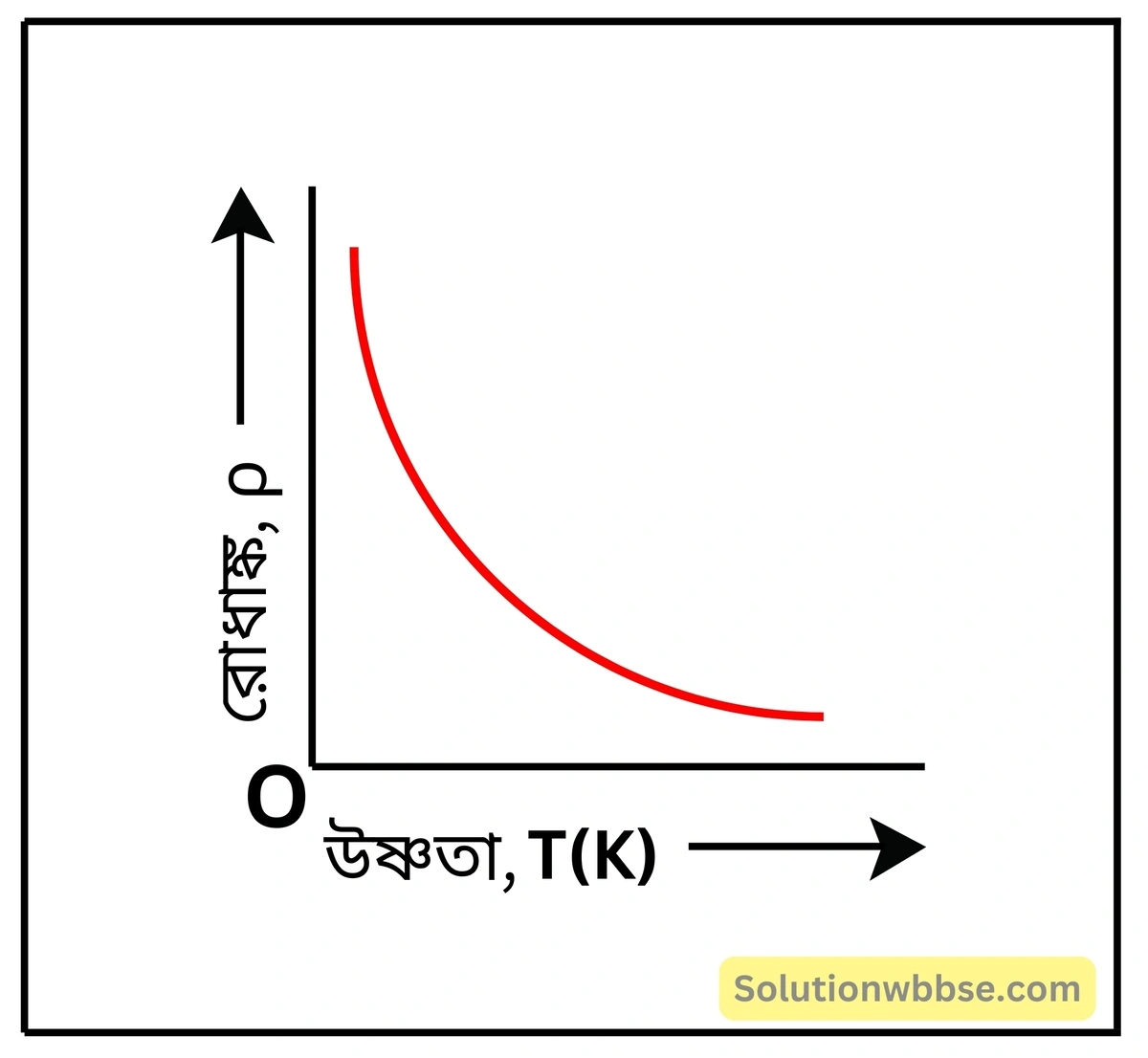
অর্ধপরিবাহীর রোধাঙ্ক সুপরিবাহীর তুলনায় বেশি কিন্তু অন্তরকের তুলনায় কম। এই ধরনের পদার্থে মুক্ত ইলেকট্রন ঘনত্ব কম। তাপমাত্রা বৃদ্ধি পেলে সমযোজী বন্ধন ভেঙে কিছু ইলেকট্রন পরমাণু থেকে বেরিয়ে আসে ফলে মুক্ত ইলেকট্রন ঘনত্ব বৃদ্ধি পায় এবং রোধাঙ্ক কমে। অর্থাৎ কোনো অর্ধপরিবাহীর তাপমাত্রা বৃদ্ধি করলে রোধাঙ্ক হ্রাস পায়। নীচের চিত্রে তাপমাত্রার পরিবর্তনের সঙ্গে অর্ধপরিবাহীর রোধাঙ্কের পরিবর্তন লেখচিত্রের সাহায্যে দেখানো হয়েছে।
অতিপরিবাহী বলতে কী বোঝ? রোধাঙ্ক-উষ্ণতা লেখচিত্র এঁকে দেখাও।
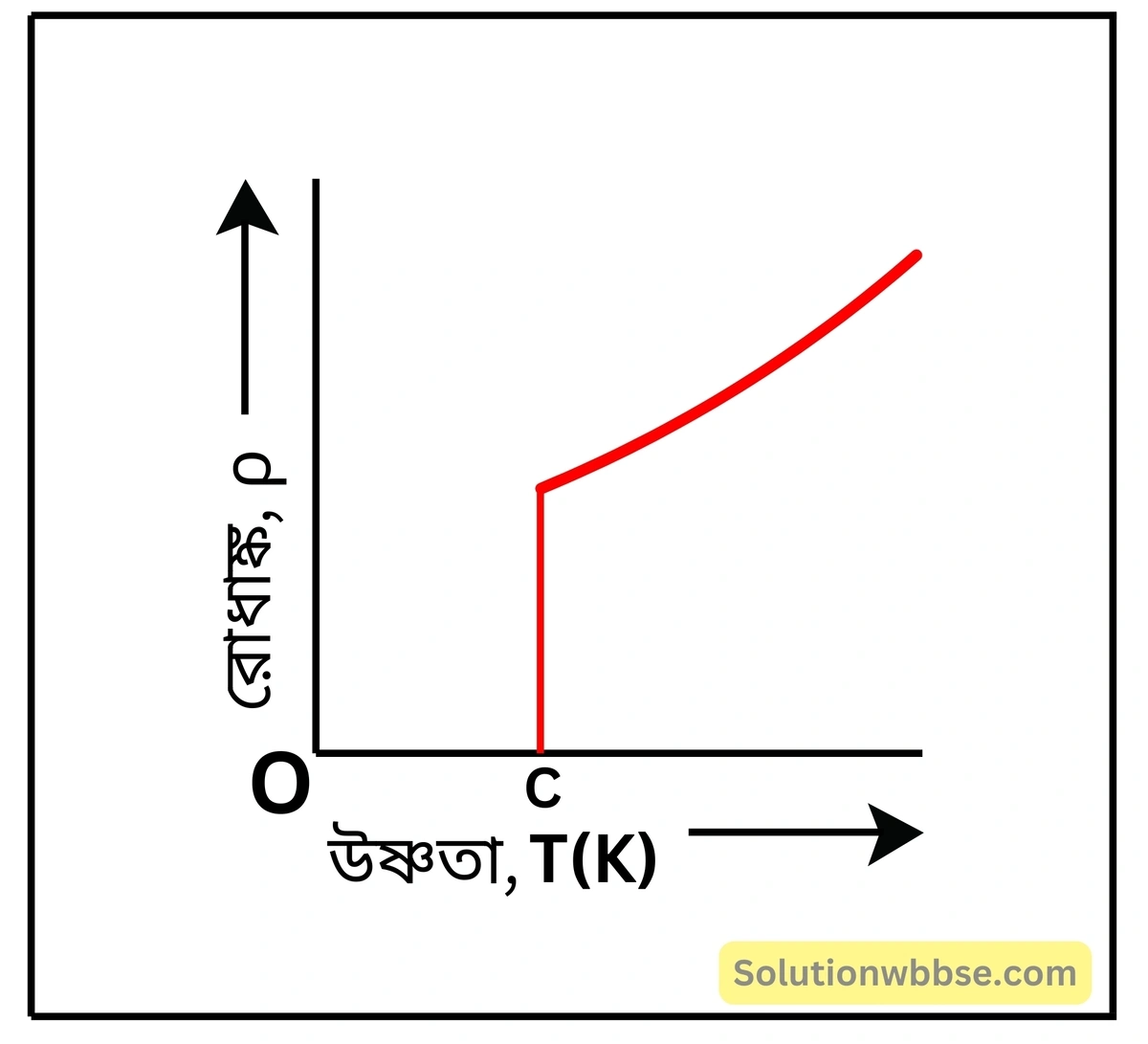
তাপমাত্রা হ্রাস করলে সাধারণত ধাতুর রোধাঙ্ক হ্রাস পায়। এক ধরনের ধাতু ও যৌগিক পদার্থ আছে যাদের তাপমাত্রা একটি নির্দিষ্ট তাপমাত্রা অপেক্ষা কম হলে রোধাঙ্ক শূন্য হয়ে যায়। এই নির্দিষ্ট উষ্ণতাকে সংকট উষ্ণতা বলা হয়। এই ধরনের ঘটনাকে অতিপরিবাহিতা এবং তখন ওই সব পদার্থকে অতিপরিবাহী বলা হয়। নীচের চিত্রে এই ধরনের পদার্থের উষ্ণতা পরিবর্তনের সঙ্গে রোধাঙ্কের পরিবর্তন লেখচিত্রের সাহায্যে দেখানো হয়েছে। লেখচিত্রে C হল সংকট উষ্ণতা। যেমন পারদ 4.2 K তাপমাত্রায়, সিসা 7 K বা নিওবিয়াম নাইট্রাইড (NbN) 16 K তাপমাত্রায় অতিপরিবাহী হয়।
রোধাঙ্ক-উষ্ণতা লেখচিত্র –
উচ্চ উষ্ণতা অতিপরিবাহিতা কাকে বলে?
1986 খ্রিস্টাব্দে বিজ্ঞানী বেডনোর্ডজ [Bednorz] এবং মুলার [Muller] আবিষ্কার করেন ইট্রিয়াম নির্ভর কিউপ্রেট পেরোক্সাইট পদার্থ [yttrium based cuprate perovskite] যা 92 K উষ্ণতায় অতিপরিবাহী হয়। এই ঘটনাকে উচ্চ উষ্ণতা অতিপরিবাহিতা বলা হয়।
তুল্য রোধ কাকে বলে?
কোনো তড়িৎবর্তনীর দুটি বিন্দুর মধ্যে সংযুক্ত একাধিক রোধের পরিবর্তে একটি রোধ ব্যবহার করে রোধটির দুই প্রান্তে একই বিভবপ্রভেদ প্রয়োগ করলে যদি একই তড়িৎপ্রবাহ পাওয়া যায় তবে ওই রোধকে উক্ত রোধগুলির তুল্য রোধ বলে।
রোধের শ্রেণি সমবায় ও সমান্তরাল সমবায় কাকে বলে?
রোধের শ্রেণি সমবায় – যদি কতকগুলি রোধ পরপর এমনভাবে যুক্ত থাকে যে, একটির শেষ প্রান্ত পরেরটির প্রথম প্রান্তের সঙ্গে যুক্ত থাকে এবং রোধগুলিকে কোনো তড়িৎবর্তনীতে যুক্ত করলে প্রতিটির মধ্য দিয়ে একই তড়িৎপ্রবাহ হয় তাহলে রোধগুলির এই সমবায়কে শ্রেণি সমবায় বলা হয়।
রোধের সমান্তরাল সমবায় – যদি কতকগুলি রোধ এমনভাবে যুক্ত থাকে যে রোধগুলির একপ্রান্ত একটি নির্দিষ্ট বিন্দুতে ও অপর প্রান্ত অপর একটি নির্দিষ্ট বিন্দুতে যুক্ত থাকে এবং কোনো তড়িৎবর্তনীতে যুক্ত করলে প্রতিটি রোধের দু-প্রান্তের বিভবপ্রভেদ একই হয় তাহলে রোধগুলির এই সমবায়কে সমান্তরাল সমবায় বলা হয়।
তিনটি রোধের শ্রেণি সমবায়ের তুল্য রোধ নির্ণয় করো।
নীচের (a) নং চিত্রে \( R_{1,}R_2 \) ও \( R_3 \) রোধ তিনটির শ্রেণি সমবায় মূল বর্তনীর সঙ্গে \( A \) ও \( D \) বিন্দুতে যুক্ত। বর্তনীর তড়িৎপ্রবাহ \( \left(I\right)\;A \) থেকে \( D \) -এর দিকে চলছে।
মনে করি, \( A,B,C \) ও \( D \) বিন্দুর তড়িৎবিভব যথাক্রমে \( V_{A,}\;V_{B,}\;V_C \) ও \( V_D \)।
ওহমের সূত্র থেকে পাই, \( V_A-V_B=IR_1 \) ___(1)
\( V_B-V_C=IR_2 \) ___(2)
\( V_C-V_D=IR_3 \) ___(3)
(1), (2) ও (3) নং সমীকরণ তিনটি যোগ করে পাই,
\( V_A-V_D=I\left(R_1+R_2+R_3\right) \) ___(4)
এই তিনটি রোধের পরিবর্তে \( A \) ও \( D \) বিন্দুর মধ্যে \( R_s \) রোধ ব্যবহার করে একই বিভবপ্রভেদ প্রয়োগ করলে যদি একই প্রবাহমাত্রা \( I \) পাওয়া যায় তাহলে \( R_s \) হল রোধ তিনটির শ্রেণি সমবায়ের তুল্য রোধ।
∴ \( V_A-V_D=IR_s \) ___(5)
(4) নং ও (5) নং সমীকরণ তুলনা করে পাই,
\( R_s=R_1+R_2+R_3 \) ___(6)
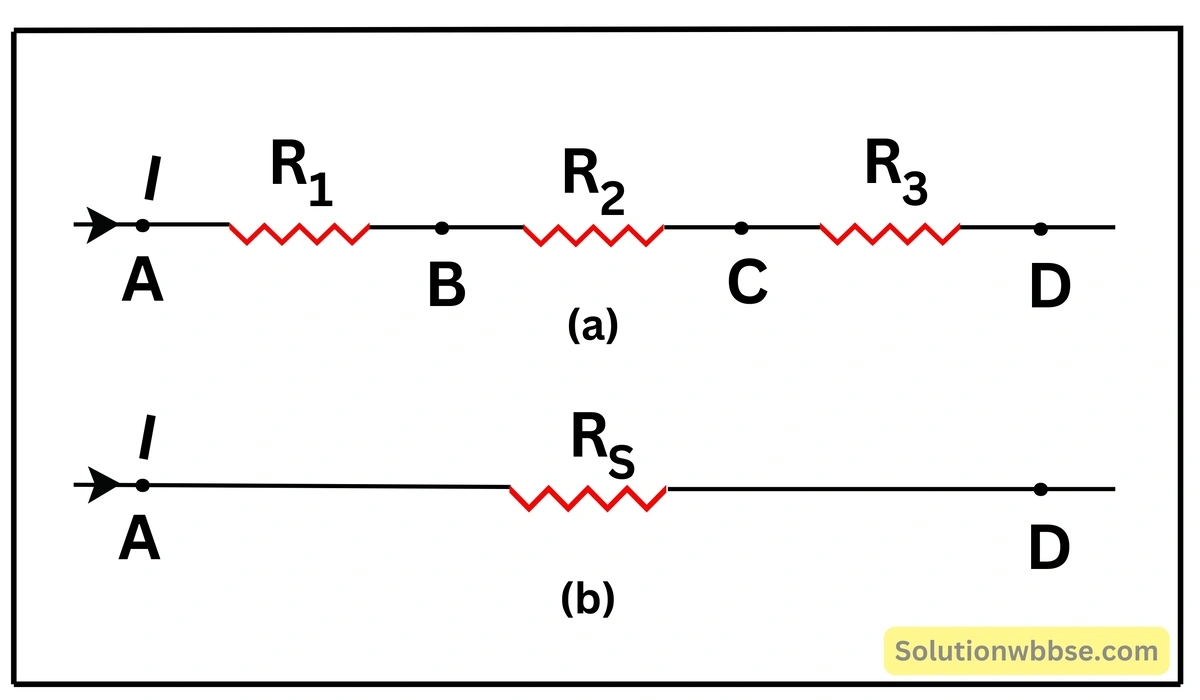
রোধের শ্রেণি সমবায়ের বৈশিষ্ট্যগুলি লেখো।
রোধের শ্রেণি সমবায়ের বৈশিষ্ট্য –
- প্রতিটি রোধের মধ্য দিয়ে একই তড়িৎপ্রবাহ হয়।
- সমবায়ের তুল্য রোধ, প্রতিটি রোধের সমষ্টির সমান।
- সমবায়ের দু-প্রান্তে বিভবপার্থক্য প্রয়োগ করলে বিভিন্ন রোধের দু-প্রান্তের বিভবপ্রভেদ, রোধের সমানুপাতিক হয়।
- সমবায়ের তুল্য রোধ, সমবায়ের প্রতিটি রোধের মানের চেয়ে বড়ো হয়।
তিনটি রোধের সমান্তরাল সমবায়ের তুল্য রোধ নির্ণয় করো।
নীচের (a) নং চিত্রে \( R_{1,}\;R_{2,}\;R_3 \) রোধ তিনটির সমান্তরাল সমবায় মূল বর্তনীর সঙ্গে \( A \) ও \( B \) বিন্দুতে যুক্ত। \( A \) ও \( B \) বিন্দুর মধ্যে বিভবপ্রভেদ, \( V_A-V_B=V \), বর্তনীর মূল প্রবাহমাত্রা \( I \) এবং \( R_{1,}R_2 \) ও \( R_3 \) রোধে প্রবাহমাত্রা যথাক্রমে \( I_{1,}\;I_2 \) ও \( I_3 \)। যেহেতু রোধগুলি সমান্তরাল সমবায়ে যুক্ত সেহেতু প্রতিটি রোধের দু-প্রান্তের বিভবপ্রভেদ সমান।
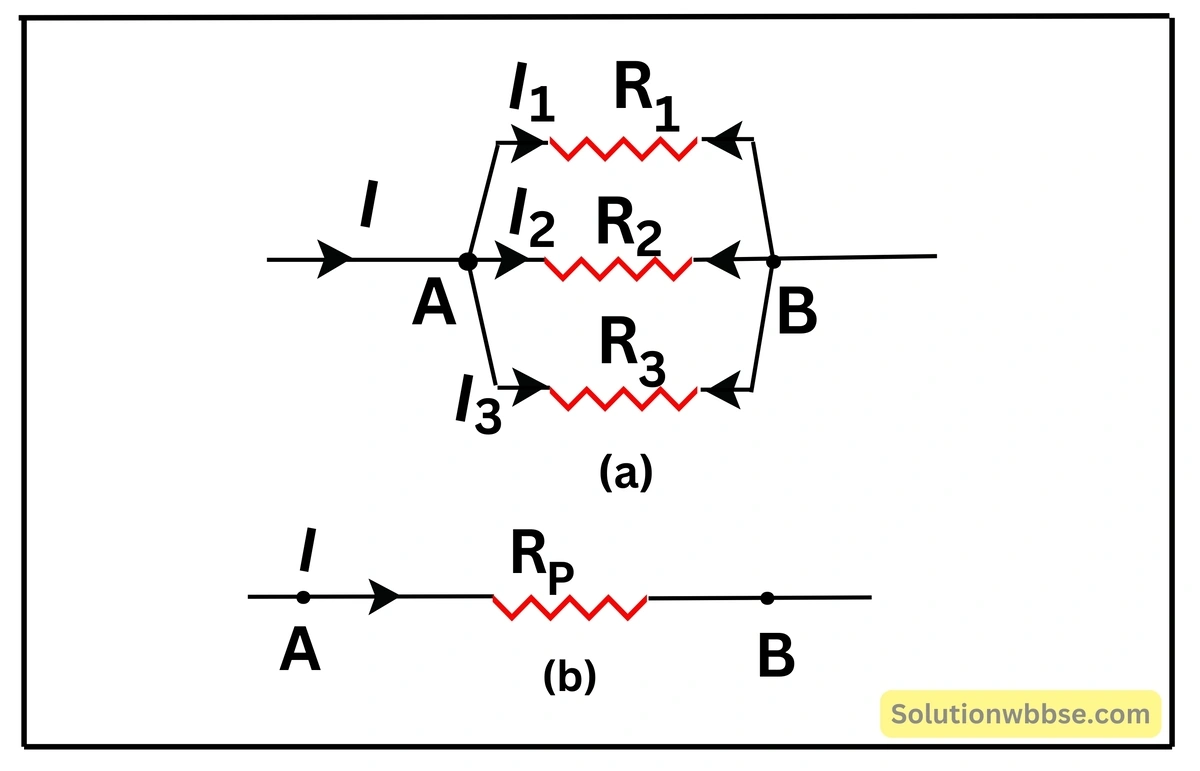
ওহমের সূত্র প্রয়োগ করে পাই,
প্রথম রোধের ক্ষেত্রে, \( V=I_1R_1 \)
বা, \( I_1=\frac V{R_1} \) ___(1)
\( R_2 \) রোধের ক্ষেত্রে, \( V=I_2R_2 \)
বা, \( I_2=\frac V{R_2} \) ___(2)
ও \( R_3 \) রোধের ক্ষেত্রে, \( V=I_3R_3 \)
বা, \( I_3=\frac V{R_3} \) ___(3)
আবার, \( I=I_1+I_2+I_3 \)
বা, \( I=\frac V{R_1}+\frac V{R_2}+\frac V{R_3} \)
বা, \( I=V\left(\frac1{R_1}+\frac1{R_2}+\frac1{R_3}\right) \) ___(4)
\( A \) ও \( B \) বিন্দুর মধ্যে তিনটি রোধের পরিবর্তে \( R_p \) মানের একটি রোধ ব্যবহার করে একই বিভবপ্রভেদ প্রয়োগ করলে যদি একই প্রবাহমাত্রা \( I \) পাওয়া যায় তাহলে \( R_p \) -কে বলা হয় রোধ তিনটির সমান্তরাল সমবায়ের তুল্য রোধ।
∴ \( V=IR_p \)
বা, \( I=\frac V{R_p} \) ___(5)
(4) নং ও (5) নং সমীকরণ তুলনা করে পাই, \( \frac1{R_p}=\frac1{R_1}+\frac1{R_2}+\frac1{R_3} \) ___(6)
রোধের সমান্তরাল সমবায়ের বৈশিষ্ট্যগুলি লেখো।
রোধের সমান্তরাল সমবায়ের বৈশিষ্ট্য –
- প্রতিটি রোধের দু-প্রান্তের বিভবপার্থক্য সমান হয়।
- সমবায়ের তুল্য রোধের অন্যোন্য, প্রতিটি রোধের অন্যোন্যের সমষ্টির সমান হয়।
- সমবায়ের তুল্য রোধ, সমবায়ের ক্ষুদ্রতম রোধটি অপেক্ষা ক্ষুদ্রতর হয়।
- যেহেতু প্রান্তীয় বিভবপ্রভেদ ধ্রুবক, তাই যে-কোনো রোধের মধ্য দিয়ে প্রবাহমাত্রা হল ওই রোধের সমানুপাতিক।
n টি R মানের রোধ শ্রেণি সমবায়ে ও সমান্তরাল সমবায়ে যুক্ত থাকলে তুল্য রোধ নির্ণয় করো। এই দুই ক্ষেত্রে তুল্য রোধের অনুপাত কত?
\( R_{1,}\;R_{2,}\;R_3 \) ,…., \( R_n \) মানের \( n \)টি রোধ শ্রেণি সমবায়ে থাকলে তুল্য রোধ যদি \( R_s \) হয় তাহলে,
\( R_s=R_1+R_2+R_3+…+R_n \\\)এখন, \( R_1=R_2=R_3=…=R_n=R \) হলে, \( R_s=nR \)।
আবার, রোধগুলির সমান্তরাল সমবায়ের তুল্য রোধ \( R_p \) হলে,
\( \frac1{R_p}=\frac1{R_1}+\frac1{R_2}+\frac1{R_3}+…+\frac1{R_n} \\\)\( R_1=R_2=R_3=…=R_n=R \) হলে,
\( \frac1{R_p}=\frac nR\\ \)বা, \( R_p=\frac Rn \)
এই দুই ক্ষেত্রে তুল্য রোধের অনুপাত, \( \frac{R_s}{R_p}=\frac{nR}{\displaystyle\frac Rn}=n^2 \)
দেখাও তিনটি রোধের সমান্তরাল সমবায়ের তুল্য রোধ সমবায়ের ক্ষুদ্রতম রোধটি অপেক্ষা ক্ষুদ্রতর।
মনে করি, \(R_{1,}R_2 \) ও \(R_3 \) মানের তিনটি রোধ সমান্তরাল সমবায়ে যুক্ত, এদের মধ্যে \(R_1 \) ক্ষুদ্রতম।
সমবায়ের তুল্য রোধ \( R_p \) হলে,
\( \frac1{R_p}=\frac1{R_1}+\frac1{R_2}+\frac1{R_3} \\\)বা, \( \frac1{R_p}=\frac1{R_1}+x\;\left[\frac1{R_2}+\frac1{R_3}=x(Suppose)\right] \)
যেখানে \( x \) একটি ধনাত্মক রাশি।
∴ \( \frac1{R_p}>\frac1{R_1} \)
বা, \( R_p<R_1 \)
∴ রোধ তিনটির সমান্তরাল সমবায়ের তুল্য রোধ সমবায়ের ক্ষুদ্রতম রোধটি অপেক্ষা ক্ষুদ্রতর।
তড়িৎকোশের অভ্যন্তরীণ রোধ ও নষ্ট ভোল্ট কাকে বলে?
অভ্যন্তরীণ রোধ – বদ্ধ বর্তনীতে যখন কোনো তড়িৎকোশ তড়িৎপ্রবাহ পাঠায় তখন তড়িৎকোশের মধ্য দিয়েও তড়িৎপ্রবাহ হয়। এই কোশের তড়িদ্দ্বার দুটির মাঝে সক্রিয় তরল বা তড়িদবিশ্লেষ্য পদার্থ এই তড়িৎপ্রবাহের বিরুদ্ধে বাধার সৃষ্টি করে। কোশের মধ্যে এই বাধাকেই অভ্যন্তরীণ রোধ বলা হয়।
নষ্ট ভোল্ট – বদ্ধ বর্তনীতে যখন কোনো তড়িৎকোশ তড়িৎপ্রবাহ পাঠায় তখন কোশের অভ্যন্তরে তড়িৎপ্রবাহ চালনা করার জন্য প্রয়োজনীয় বিভবপ্রভেদ, কোশের EMF ও বহির্বর্তনীর তড়িদ্দ্বার দুটির বিভবপ্রভেদের বিয়োগফলের সমান, একে কোশের নষ্ট ভোল্ট বলা হয়।
E তড়িৎচালক বল ও r অভ্যন্তরীণ রোধবিশিষ্ট একটি তড়িৎকোশের সহিত R রোধ যুক্ত করা হলে R রোধের প্রবাহমাত্রার রাশিমালাটি প্রতিষ্ঠা করো। এখানে নষ্ট ভোল্টের মান কত?
মনে করি, \( E \) তড়িৎচালক বলবিশিষ্ট একটি তড়িৎকোশকে নগণ্য রোধের পরিবাহী তার দ্বারা একটি রোধ \( R \) -এর সঙ্গে যুক্ত করা হল। এর ফলে বর্তনীতে একটি স্থির মানের তড়িৎপ্রবাহ \( I \) চলবে। এই তড়িৎপ্রবাহ বহির্বর্তনীতে কোশের ধনাত্মক মেরু থেকে ঋণাত্মক মেরুর দিকে এবং কোশের অভ্যন্তরে ঋণাত্মক মেরু থেকে ধনাত্মক মেরুর দিকে হয়। বর্তনীতে যখন তড়িৎপ্রবাহ পরিমাপ করা হয় তখন বর্তনীর মোট রোধ হিসেবে কোশের বাইরের বর্তনীর রোধ \( R \) ও কোশের অভ্যন্তরীণ রোধ \( r \) -এর সমষ্টিকে ধরা হয়।
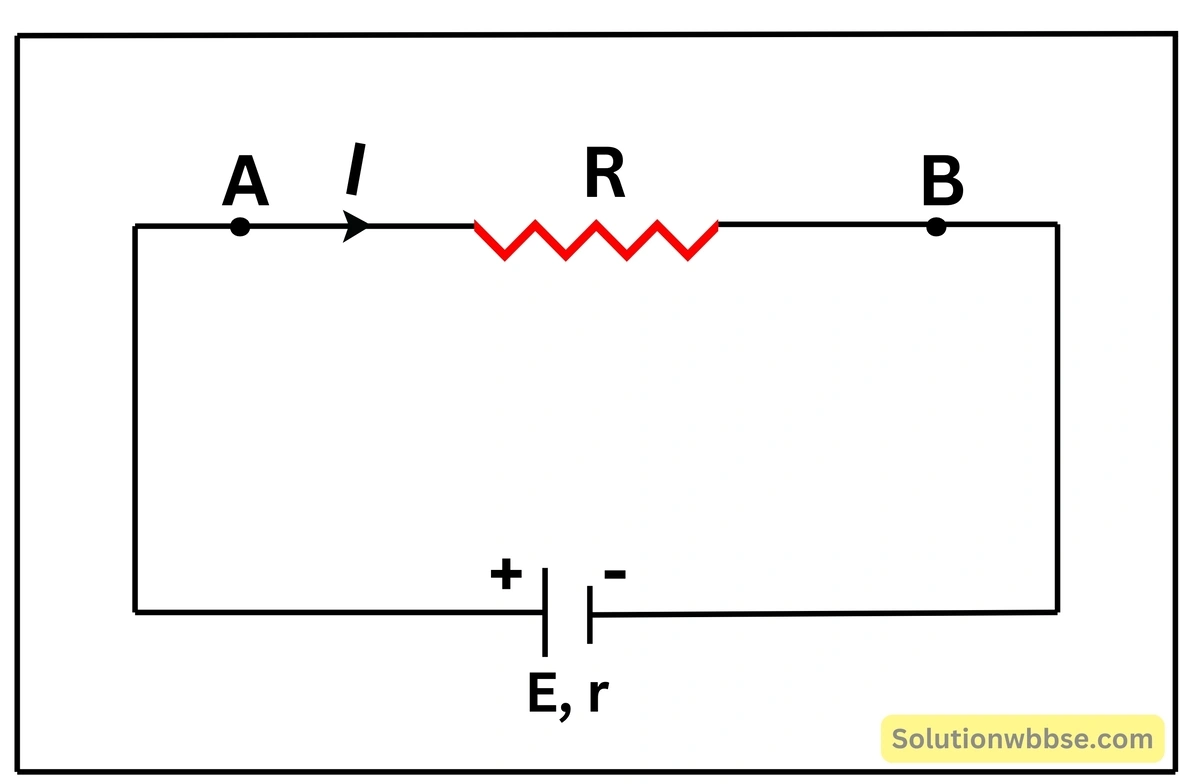
সুতরাং, বর্তনীর প্রবাহমাত্রা, \( I=\frac E{R+r} \) ___(1)
(1) নং সমীকরণ থেকে পাওয়া যায়,
\( IR=Ir=E \\\)বা, \( rI=E-RI \)
∴ নষ্ট ভোল্ট, \( rI=E-RI \)
দেখাও কোনো তড়িৎকোশের EMF হল V = IR এবং v = Ir কার্যের যোগফল। এখান থেকে EMF -এর সংজ্ঞা দাও। R = 0 হলে কী হবে?
\( E \) তড়িৎচালক বল ও \( r \) অভ্যন্তরীণ রোধবিশিষ্ট একটি তড়িৎকোশের সঙ্গে \( R \) রোধ যুক্ত করা হলে, \( R \) রোধের মধ্য দিয়ে তড়িৎপ্রবাহ
\( I=\frac E{R+r} \\\)বা, \( E=RI+rI \) ___(1)
(1) নং সমীকরণ থেকে দেখা যাচ্ছে বহির্বর্তনীতে কোশ দ্বারা সৃষ্ট বিভবপ্রভেদ, \( V=RI \) এবং নষ্ট ভোল্ট, \( v=rI \)। কোশের \( EMF \), \( E \) হল \( V=RI \) ও \( v=rI \) -এর সমষ্টি। \( V=RI \) হল একক ধনাত্মক আধানকে কোশের ধনাত্মক মেরু থেকে রোধ \( R \) -এর মধ্য দিয়ে ঋণাত্মক মেরুতে নিয়ে যেতে কোশ দ্বারা কৃত কার্য এবং \( v=rI \) হল একক ধনাত্মক আধানকে কোশের ঋণাত্মক মেরু থেকে কোশের মধ্য দিয়ে ধনাত্মক মেরুতে নিয়ে যেতে কোশ দ্বারা কৃত কার্য।
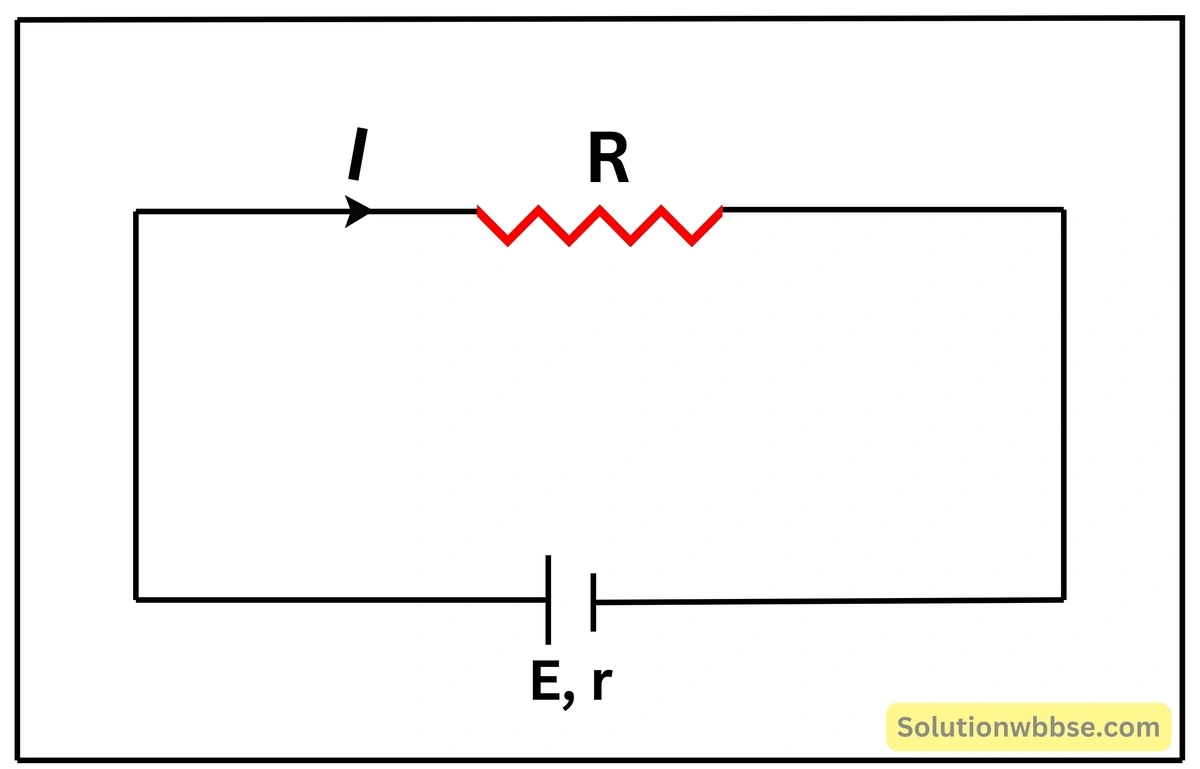
একক ধনাত্মক আধানকে কোশের ধনাত্মক মেরু থেকে বাহ্যিক রোধের মধ্য দিয়ে তড়িৎবর্তনীতে একবার ঘুরিয়ে আনতে কোশ দ্বারা কৃত কার্য-ই হল কোশের \( EMF \) -এর সমান।
বহির্বর্তনীর রোধ \( R=0 \) হলে, \( E=rI \) হয় অর্থাৎ ওই বর্তনীতে একটি তড়িৎকোশের মেরু দুটির মধ্যে বিভবপ্রভেদই হল কোশের \( EMF\)।
একটি তড়িৎকোশের তড়িৎচালক বল E ও অভ্যন্তরীণ রোধ r। কোশের সর্বোচ্চ প্রবাহমাত্রা কত?
তড়িৎকোশের দু-প্রান্তে \( R \) রোধ যুক্ত করা হলে তড়িৎপ্রবাহ,
\( I=\frac E{R+r}\\ \)যদি তড়িৎকোশের দুটি মেরুকে নগণ্য রোধের কোনো পরিবাহী তার দিয়ে যুক্ত করা হয় তাহলে \( R\approx0 \) হয়। তখন বর্তনীতে প্রবাহমাত্রা, \( I=\frac Er \)। এটিই হল কোশের সর্বোচ্চ প্রবাহমাত্রা।
তড়িৎকোশের জ্ঞাতব্য বিষয় গুলি কী কী?
- একটি তড়িৎকোশের তড়িৎচালক বলের মান তড়িৎকোশের সক্রিয় উপাদান ও তড়িদ্দ্বারের প্রকৃতির ওপর নির্ভরশীল, কোশের আয়তন বা সক্রিয় উপাদানগুলির পরিমাণের ওপর নির্ভরশীল নয়।
- একটি তড়িৎকোশের অভ্যন্তরীণ রোধ নিম্নলিখিত বিষয়গুলির ওপর নির্ভরশীল – তড়িদ্দ্বারের আকার, তড়িদ্দ্বার দুটির ব্যবধান ও সক্রিয় তরলের প্রকৃতি। তড়িৎকোশের তড়িদ্দ্বারের আকার বড়ো এবং তড়িদ্দ্বারগুলির ব্যবধান কম হলে অভ্যন্তরীণ রোধ কম হয়।
- কোনো তড়িৎকোশে সক্রিয় তড়িদবিশ্লেষ্য ও তড়িদ্দ্বার দুটির স্পর্শতলে তড়িৎচালক বল অবস্থান করে।
একটি তড়িৎকোশের তড়িৎচালক বল E ও অভ্যন্তরীণ রোধ r কোশটিকে একটি বাহ্যিক রোধের সঙ্গে যুক্ত করা হল। বাহ্যিক রোধে বিভবপার্থক্য কোশের তড়িৎচালক বলের অর্ধেক হলে বাহ্যিক রোধের মান কত?
মনে করি, বাহ্যিক রোধের মান \( =R \)।
বর্তনীতে তড়িৎপ্রবাহ, \( I=\frac E{R+r} \)
\( R \) রোধের দু-প্রান্তে বিভবপ্রভেদ \( =RI=\frac{RE}{R+r} \)
শর্তানুসারে, \( \frac{RE}{R+r}=\frac E2 \)
বা, \( R+r=2R \)
বা, \( r=R \)
বা, \( R=r \)
\( R_1 \) ও \( R_2 \) দুটি রোধ সমান্তরাল সমবায়ে যুক্ত। সমবায়টির সঙ্গে একটি তড়িৎকোশ যুক্ত করায় বর্তনীর মূল প্রবাহ হয় \( I \)। \( R_1 \) ও \( R_2 \) রোধের মধ্য দিয়ে তড়িৎপ্রবাহ নির্ণয় করো।
মনে করি, \( R_1 \) ও \( R_2 \) রোধের মধ্য দিয়ে প্রবাহমাত্রা যথাক্রমে \( I_1 \) ও \( I_2 \)।
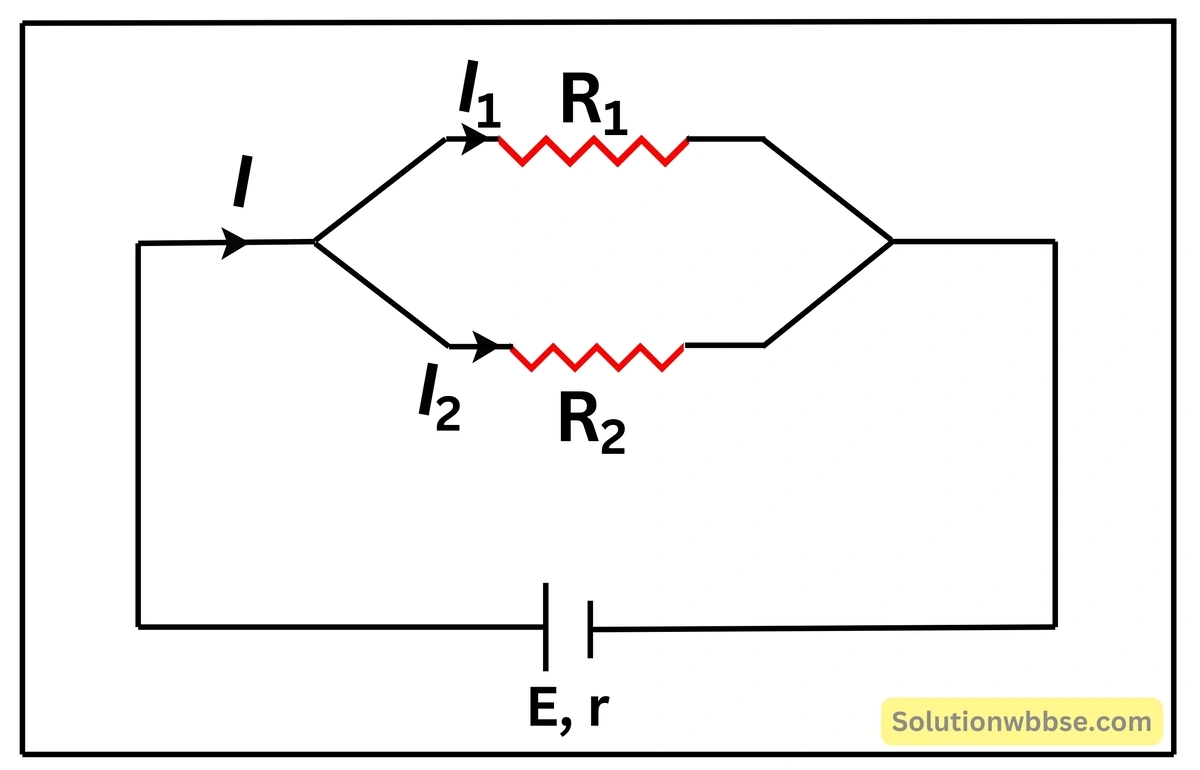
∴ \( I=I_1+I_2 \)
বা, \( I_2=I-I_1 \) ___(1)
\( R_1 \) ও \( R_2 \) রোধদুটি সমান্তরাল সমবায়ে যুক্ত, তাই দু-প্রান্তের বিভবপ্রভেদ সমান হবে।
∴ \( I_1R_1=I_2R_2 \)
বা, \( I_1R_1=\left(I-I_1\right)R_2 \)
বা, \( I_1R_1=IR_2-I_1R_2\)
বা, \( I_1R_1+I_1R_2=R_2I \)
বা, \( I_1\left(R_1+R_2\right)=R_2I \)
বা, \( I_1=\frac{R_2}{R_1+R_2}\cdot I \)
\(∴ I_2=I-I_1\\\)বা, \( I_2=I-\frac{R_2}{R_1+R_2}\cdot I \)
বা, \( I_2=\frac{R_1I+R_2I-R_2I}{R_1+R_2} \)
বা, \( I_2=\frac{R_1}{R_1+R_2}\cdot I \)
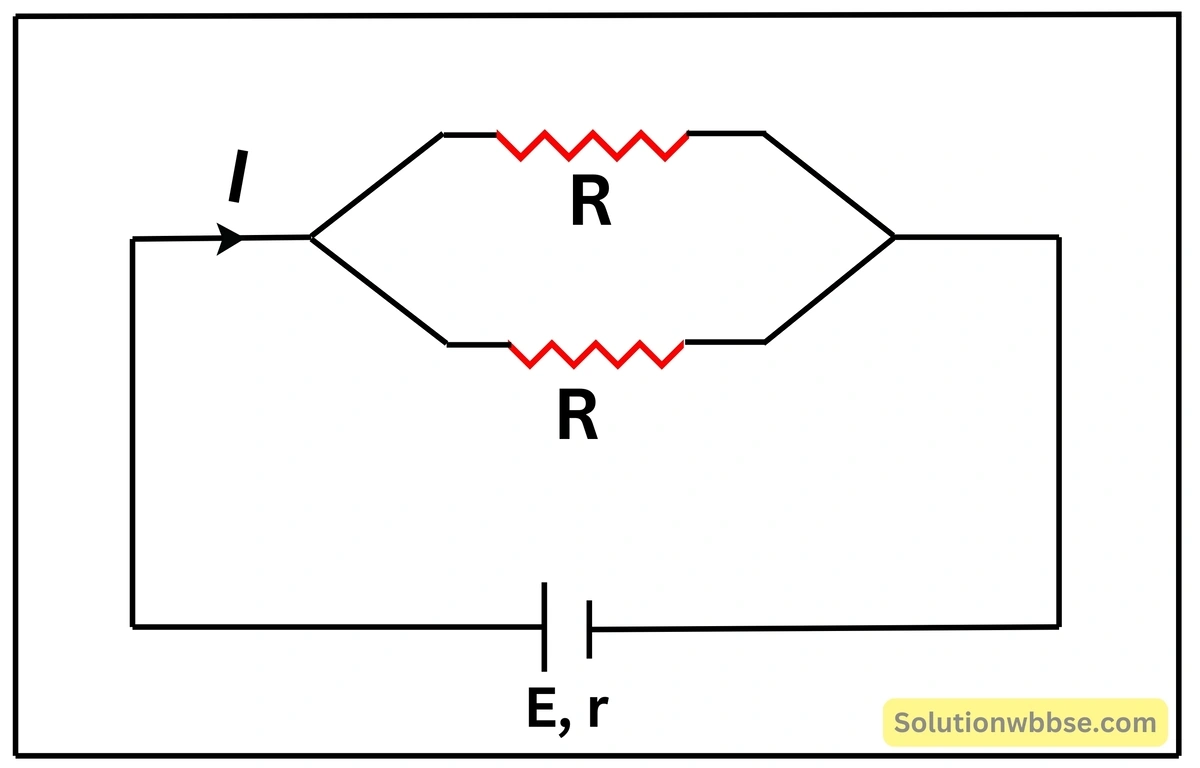
চিত্রে প্রদর্শিত বর্তনীতে R = r হলে I -এর মান নির্ণয় করো।
বহির্বর্তনীর তুল্য রোধ \( R_1 \) হলে, \( \frac1{R_1}=\frac1R+\frac1R \)
বা, \( \frac1{R_1}=\frac2R \)
বা, \( R_1=\frac R2=\frac r2 \)
∴ \( I=\frac E{R_1+r} \)
বা, \( I=\frac E{{\displaystyle\frac r2}+r} \)
বা, \( I=\frac E{\displaystyle\frac{3r}2} \)
বা, \( I=\frac{2E}{3r} \)
তড়িৎপ্রবাহের তাপীয় ফল ও তড়িৎক্ষমতা
তড়িৎপ্রবাহের তাপীয় ফল সংক্রান্ত জুলের সূত্রগুলি লেখো এবং সমীকরণের আকারে প্রকাশ করো।
1841 খ্রিস্টাব্দে ইংরেজ পদার্থবিদ জেমস প্রেসকট জুল তড়িৎপ্রবাহের তাপীয় ফল সংক্রান্ত তিনটি সূত্র প্রকাশ করেন। সূত্রগুলি হল –
- প্রবাহমাত্রার সূত্র – কোনো পরিবাহীর রোধ \( \left(R\right) \) ও তড়িৎপ্রবাহের সময় \( \left(t\right) \) স্থির থাকলে পরিবাহীতে উৎপন্ন তাপ \( \left(H\right) \), প্রবাহমাত্রার \( \left(I\right) \) বর্গের সমানুপাতিক। অর্থাৎ \( H\propto I^2 \) [যখন R এবং t ধ্রুবক]।
- রোধের সূত্র – কোনো পরিবাহীর মধ্য দিয়ে প্রবাহমাত্রা \(\left(I\right) \) ও তড়িৎপ্রবাহের সময় \(\left(t\right) \) স্থির থাকলে পরিবাহীতে উৎপন্ন তাপ \(\left(H\right) \), পরিবাহীর রোধের \(\left(R\right) \) সমানুপাতিক। অর্থাৎ \(H\propto R\) [যখন \( I \) এবং \( t \) ধ্রুবক]।
- সময়ের সূত্র – কোনো পরিবাহীর রোধ \( \left(R\right) \) ও প্রবাহমাত্রা \( \left(I\right) \) স্থির থাকলে পরিবাহীতে উৎপন্ন তাপ \( \left(H\right) \), তড়িৎপ্রবাহের সময়ের \( \left(t\right) \) সমানুপাতিক। অর্থাৎ \( H\propto t \) [যখন \( R \) এবং \( I \) ধ্রুবক]।
সূত্র তিনটি থেকে যৌগিক ভেদের নিয়মানুযায়ী পাই,
\( H\propto I^2Rt \) [যখন \( I,R \) ও \( t \) তিনটিই পরিবর্তনশীল]
বা, \( H=\frac{I^2Rt}J \)
যেখানে \( J \) একটি ধ্রুবক, যাকে তাপের যান্ত্রিক তুল্যাঙ্ক বলা হয়। কার্য বা শক্তিকে জুল \( \left(J\right) \) এককে এবং তাপকে ক্যালোরি (cal) এককে প্রকাশ করা হলে, \( J=4.2\;J/cal \)
∴ \( H=\frac{I^2Rt}{4.2}cal \)
যেখানে \( I \) -এর একক \( A,R \) -এর একক \( \Omega \) ও \( t \) এর একক \( s \)।
কার্যের ধারণা থেকে তড়িৎপ্রবাহের তাপীয় ফল সংক্রান্ত জুলের সূত্রটি প্রতিষ্ঠা করো।
মনে করি, \( R \) রোধের দুই প্রান্ত \( A \) ও \( B \) -এর সঙ্গে একটি তড়িৎকোশ যুক্ত যার তড়িৎচালক বল \( E \) ও অভ্যন্তরীণ রোধ \( r \)। \( A \) ও \( B \) বিন্দুর তড়িৎবিভব যথাক্রমে \( V_A \) ও \( V_B \) হলে \( V_A>V_B \) এবং \( A \) ও \( B \) বিন্দুর মধ্যে বিভবপ্রভেদ, \( V=V_A-V_B \)। বর্তনীতে প্রবাহমাত্রা \( I \) ও \( R \) রোধের মধ্য দিয়ে \( t \) সময়ে প্রবাহিত আধান \( q \) হলে, \( I=\frac qt \)
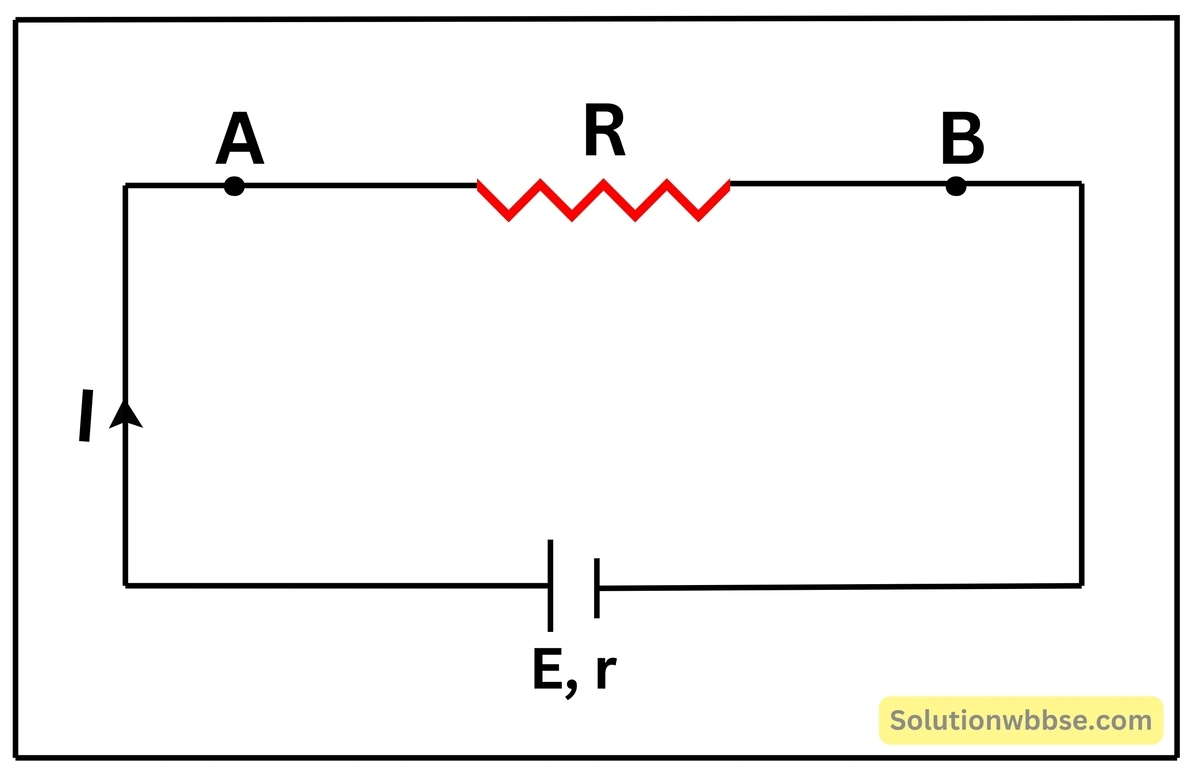
অর্থাৎ \( q=It \) ___(1)
এই \( q \) আধানকে \( V \) বিভবপ্রভেদের মধ্য দিয়ে নিয়ে যেতে তড়িৎকোশকে কার্য সম্পাদন করতে হয়।
∴ তড়িৎকোশ দ্বারা কৃত কার্য, \( W=qV \)
বা, \( W=VIt \) ___(2)
এবার ওহমের সূত্র থেকে পাই, \( V=IR \)।
∴ \( W=IR\cdot It \)
বা, \( W=I^2Rt \) ___(3)
তড়িৎকোশ দ্বারা এই কৃত কার্য তাপশক্তিতে রূপান্তরিত হয়। উৎপন্ন তাপ \( H \) হলে, তাপ ও কার্যের তুল্যতা থেকে পাই,
\( W=JH \\\)বা, \( H=\frac WJ \)
বা, \( H=\frac{I^2Rt}J \) ___(4)
যেখানে \( J=4.2\;J/Cal \) হল তাপের যান্ত্রিক তুল্যাঙ্ক।
∴ \( H=\frac{I^2Rt}{4.2}cal \) ___(5)
আবার \( SI \) -তে তাপ ও কার্য উভয়েরই একক \( J \) (জুল), তাই উৎপন্ন তাপ \( \left(H\right)J \) এককে প্রকাশ করা হলে,
\( H=I^2Rt\;J \) ___(6)
(4), (5) বা 6 নং সমীকরণ হল তড়িৎপ্রবাহের তাপীয় ফল সংক্রান্ত জুলের সূত্র।
জুলের সূত্র থেকে তাপের যান্ত্রিক তুলাঙ্কের (J) সংজ্ঞা দাও।
\( R \) রোধের কোনো পরিবাহীর মধ্য দিয়ে \( t \) সময় ধরে \( I \) তড়িৎপ্রবাহ হলে যদি \( H \) তাপ উৎপন্ন হয় তাহলে জুলের সূত্রানুযায়ী,
\( H=\frac{I^2Rt}J \\\)বা, \( J=\frac{I^2Rt}H \) ___(1)
(1) নং সমীকরণে, \( I=1,R=1 \) ও \(t=1 \) হলে \( J=\frac1H \)।
অর্থাৎ একক রোধের কোনো পরিবাহীর মধ্য দিয়ে একক তড়িৎপ্রবাহ, একক সময় ধরে পাঠালে যে তাপ উৎপন্ন হয় তার অন্যোন্যকে তাপের যান্ত্রিক তুল্যাঙ্ক বলা হয়।
তড়িৎপ্রবাহের তাপীয় ফল সংক্রান্ত জুলের সূত্রে তড়িৎপ্রবাহের অভিমুখ বিপরীত করলে কী হবে?
জুলের সূত্রানুযায়ী, পরিবাহীর রোধ \( \left(R\right) \) ও সময় \( \left(t\right) \) অপরিবর্তিত থাকলে উৎপন্ন তাপ \( \left(H\right) \), প্রবাহমাত্রার \( \left(I\right) \) বর্গের সমানুপাতিক। তাই প্রবাহমাত্রা বিপরীত করলেও উৎপন্ন তাপ একই থাকবে।
কতকগুলি রোধ সমান্তরাল সমবায়ে থাকলে উৎপন্ন তাপের ওপর কীভাবে নির্ভর করে?
\( R \) রোধের কোনো পরিবাহীর মধ্য দিয়ে \( t \) সময় ধরে \( I \) তড়িৎপ্রবাহ হলে জুলের সূত্রানুযায়ী উৎপন্ন তাপ,
\( H=I^2Rt \) [উৎপন্ন তাপ \(J \) এককে প্রকাশিত] ___(1)
কতকগুলি রোধ সমান্তরাল সমবায়ে থাকলে রোধগুলির প্রতিটির দু-প্রান্তের বিভবপ্রভেদ, \( V \) স্থির থাকে।
আবার, \( V=IR \)
বা, \( I=\frac VR \)
(1) নং সমীকরণ থেকে পাই,
\( H=\frac{V^2}{R^2}\cdot R\cdot t \\\)বা, \( H=\frac{V^2}R\cdot t \) ___(2)
(2) নং সমীকরণ থেকে পাই, \( H\propto\frac1R \) [যখন V ও t স্থির]
অর্থাৎ কতকগুলি রোধ সমান্তরাল সমবায়ে থাকলে উৎপন্ন তাপ, রোধের ব্যস্তানুপাতিক হয়।
কোনো পরিবাহীর মধ্য দিয়ে তড়িৎপ্রবাহ হলে তাপ উৎপন্ন হয় কেন?
সাধারণত কোনো পরিবাহীতে মুক্ত ইলেকট্রনগুলি হল তড়িতের বাহক। পরিবাহীর দু-প্রান্তে বিভবপ্রভেদ প্রয়োগ করলে মুক্ত ইলেকট্রনগুলি নিম্নবিভব থেকে উচ্চবিভবের দিকে গতিশীল হয়। এইসময় মুক্ত ইলেকট্রনগুলি পরিবাহীর অণুগুলির সঙ্গে সংঘর্ষ ঘটায় এবং অণুগুলির স্পন্দনজনিত গতিশক্তি বৃদ্ধি পায়। গতিশক্তি বৃদ্ধি পাওয়ার অর্থ হল উষ্ণতা বৃদ্ধি, ফলে পরিবাহীতে তাপ উৎপন্ন হয়।
পরিবাহীর প্রস্থচ্ছেদের ক্ষেত্রফল ও উৎপন্ন তাপের মধ্যে সম্পর্ক স্থাপন করো।
কতকগুলি রোধ শ্রেণি সমবায়ে থাকলে প্রতিটি রোধের মধ্য দিয়ে তড়িৎপ্রবাহ \(\left(I\right) \) স্থির থাকে।
∴ উৎপন্ন তাপ, \(H\propto R \) [যখন, \(I,\;t \) স্থির]
আবার পরিবাহীর রোধ, \( R=\rho\frac lA \) যেখানে \( \rho \) হল পরিবাহীর উপাদানের রোধাঙ্ক, \( l \) হল দৈর্ঘ্য ও \( A \) হল প্রস্থচ্ছেদের ক্ষেত্রফল।
∴ এক্ষেত্রে \( H\propto l \) [যখন, \( I,\;A,\;t \) স্থির]
ও \( H\propto\frac1A \) [যখন, \( I,\;l,t \) স্থির]
আবার কতকগুলি রোধ সমান্তরাল সমবায়ে থাকলে প্রতিটি রোধের দু-প্রান্তের বিভবপ্রভেদ \( \left(V\right) \) স্থির থাকে।
∴ উৎপন্ন তাপ \( H\propto\frac1R\) [যখন, \(V,\;t \) স্থির]
∴ এক্ষেত্রে, \(H\propto\frac1l \) [যখন,\( V,\;A,\;t\) স্থির]
ও \(H\propto A \) [যখন,\(V,\;l,\;t \) স্থির]
তড়িৎক্ষমতা কাকে বলে? তড়িৎক্ষমতার রাশিমালাটি প্রতিষ্ঠা করো।
কোনো তড়িৎযন্ত্রের সময়ের সাপেক্ষে বৈদ্যুতিক শক্তি ব্যয়ের হারকে তড়িৎক্ষমতা বলা হয়।
কোনো তড়িৎযন্ত্র কোনো পরিবাহীর মধ্য দিয়ে \( t \) সময় ধরে \( I \) তড়িৎপ্রবাহ পাঠালে ব্যয়িত তড়িৎশক্তি, \( W=VIt \), যেখানে \( V \) হল পরিবাহীর দুই প্রান্তের বিভবপ্রভেদ।
∴ তড়িৎক্ষমতা, \( P=\frac Wt \)
বা, \( P=\frac{VIt}t \)
বা, \( P=VI \)
অর্থাৎ, তড়িৎক্ষমতা = বিভবপ্রভেদ × প্রবাহমাত্রা
আবার, পরিবাহীর রোধ \( R \) হলে, \( V=IR \)
∴ \( P=IR\cdot I=I^2R \)
আবার, \( I=\frac VR \)
সুতরাং, \( I=\frac{V^2}{R^2}\cdot R \)
বা, \( P=\frac{V^2}R \)
∴ তড়িৎক্ষমতা, \( P=VI=I^2R=\frac{V^2}R \)
SI -তে তড়িৎক্ষমতার এককের সংজ্ঞা লেখো।
SI -তে তড়িৎক্ষমতার একক হল W (বা watt)।
তড়িৎবর্তনীর কোনো অংশে 1 V বিভবপ্রভেদের মধ্য দিয়ে 1 A তড়িৎপ্রবাহ পাঠাতে যে ক্ষমতার প্রয়োজন হয় বা 1 Ω রোধের মধ্য দিয়ে 1 A তড়িৎপ্রবাহ চালনা করতে যে ক্ষমতার প্রয়োজন হয় বা 1 Ω রোধের দুই প্রান্তে 1 V বিভবপ্রভেদ বজায় রাখতে যে ক্ষমতার প্রয়োজন হয় তাকে 1 W বলা হয়।
\( W\cdot h,\;kW\cdot h \) বা BOT একক (board of trade unit) কাকে বলে? এগুলি কোন্ ভৌতরাশির একক?
\( 1\;W\cdot h \) – 1 W (বা watt) ক্ষমতাসম্পন্ন একটি তড়িৎযন্ত্র 1 h (hour) চললে যে বৈদ্যুতিক শক্তি ব্যয় করে তাকে \( 1\;W\cdot h \) বলা হয়।
\( 1\;W\cdot h \) বা BOT একক – 1 kW ক্ষমতাসম্পন্ন একটি তড়িৎযন্ত্র 1 h (hour) চললে যে বৈদ্যুতিক শক্তি ব্যয় হয় তাকে \( 1\;kW\cdot h \) বা BOT একক বলা হয়।
\( W\cdot h \) ও \( kW\cdot h \) বা BOT একক হল তড়িৎশক্তির একক।
\( 1\;W\cdot h \) ও \( 1\;kW\cdot h \) -কে ‘J’ এককে প্রকাশ করো।
\( 1\;W\cdot h=1\frac Js\times3600s=3600J \\\)এবং \( 1\;kW\cdot h=1000\;W\cdot h\)
বা, \( 1\;kW\cdot h=1000\frac Js\times3600s \)
∴ \( 1\;kW\cdot h=3.6\times10^6\;J \)
MW ও kW কোন ভৌতরাশির একক? MW -কে kW এককে প্রকাশ করো।
MW ও kW হল তড়িৎক্ষমতার ব্যাবহারিক একক।
\( 1\;MW=10^6\;W \\\)বা, \( 1\;MW=10^3\cdot10^3\;W \)
∴ \( 1\;MW=1000\;kW \)
একটি বৈদ্যুতিক বাতির কীভাবে মূল্যায়নকরণ করা হয়?
অথবা, একটি বৈদ্যুতিক বাতির ভোল্টেজ রেটিং ও ক্ষমতা রেটিং বলতে কী বোঝ?
যে-কোনো বৈদ্যুতিক যন্ত্রই এমনভাবে তৈরি করা হয় যাতে একটি নির্দিষ্ট বিভবপ্রভেদে যন্ত্রটি ক্ষতিগ্রস্ত না হয়ে সবচেয়ে বেশি কার্যকর হয়। যন্ত্রের গায়ে এই নির্দিষ্ট বিভবপ্রভেদের মান লেখা থাকে। একে ভোল্টেজ রেটিং বলা হয়।
কোনো বৈদ্যুতিক বাতির গায়ে 220 V লেখা থাকলে বুঝতে হবে বাতিটিকে 220 V -এর সরবরাহ লাইনে যুক্ত করলে বাতিটি ক্ষতিগ্রস্ত না হয়ে সবচেয়ে বেশি কর্মক্ষম হবে। বিভবপ্রভেদ 220 V -এর কম হলে এটি কম উজ্জ্বলভাবে জ্বলবে এবং বিভবপ্রভেদ 220 V -এর বেশি হলে বাতিটি ক্ষতিগ্রস্ত বা পুড়ে যেতে পারে।
ভোল্টেজ রেটিং ছাড়া বাতির গায়ে আরও একটি রেটিং থাকে, সেটি হল ক্ষমতা রেটিং। এটিকে ওয়াট রেটিংও বলা হয়।
কোনো বৈদ্যুতিক বাতিকে যে ভোল্টেজ রেটিং -এ তৈরি করা হয়েছে সেই বিভবপ্রভেদ প্রয়োগ করলে বৈদ্যুতিক বাতিটি একক সময়ে যে তড়িৎশক্তি ব্যয় করে তাই হল বাতিটির ক্ষমতা রেটিং বা ওয়াট রেটিং।
কোনো বৈদ্যুতিক বাতির গায়ে 220 V-100 W লেখা আছে। এর থেকে কী জানা যায়?
কোনো বৈদ্যুতিক বাতির গায়ে 220 V-100 W লেখা থাকলে বোঝা যায়, বাতিটির দু-প্রান্তের বিভবপ্রভেদ 220 V হলে বাতিটি সবচেয়ে উজ্জ্বলভাবে জ্বলবে এবং বাতিটি প্রতি সেকেন্ডে 100 J তড়িৎশক্তি ব্যয় করবে।
কয়েকটি তড়িৎযন্ত্রের ভোল্টেজ রেটিং ও ক্ষমতা রেটিং
| তড়িৎযন্ত্র | ভোল্টেজ রেটিং (V) | ক্ষমতা রেটিং (W) |
| বৈদ্যুতিক বাতি | 220 | 10-200 |
| বৈদ্যুতিক পাখা | 220 | 70-100 |
| হিটার | 220 | 1000-2000 |
| মিক্সার | 220 | 750 |
| TV | 220 | 100-120 |
| টিউবলাইট | 220 | 40 |
| ফ্রিজ | 220 | 120-150 |
| গিজার | 220 | 1500 |
220 V-100 W বাতির রোধ ও সর্বোচ্চ প্রবাহমাত্রা নির্ণয় করো।
বাতির রেটিং 220 V-100 W – অর্থাৎ বাতির দু-প্রান্তের বিভবপ্রভেদ V = 220 V হলে ব্যয়িত ক্ষমতা হবে, P = 100 W।
বাতিটির রোধ R হলে,
\( P=\frac{V^2}R \\\)বা, \( R=\frac{V^2}P \)
বা, \( R=\frac{200^2}{100}=484\Omega \)
বাতিটির সর্বোচ্চ প্রবাহমাত্রা \( I \) হলে,
\( P=VI \\\)বা, \( I=\frac PV \)
বা, \( I=\frac{100}{220}=0.454\;A \)
240 V-60 W ও 240 V-100 W -এর দুটি বৈদ্যুতিক বাতিকে শ্রেণি সমবায়ে যুক্ত করা হলে কোন্ বাতিটি অধিকতর উজ্জ্বলভাবে জ্বলবে?
\( R \) রোধের কোনো বাতির দুই প্রান্তে \( V \) বিভবপ্রভেদ প্রয়োগ করলে যদি ব্যয়িত ক্ষমতা \( P \) হয় তবে
\( P=\frac{V^2}R \\\)বা, \( R=\frac{V^2}P \) ___(1)
(1) নং সমীকরণ থেকে পাই,
প্রথম বাতির রোধ, \( R_1=\frac{240^2}{60}=960\;\Omega \)
ও দ্বিতীয় বাতির রোধ, \( R_2=\frac{240^2}{100}=576\;\Omega \)
বাতি দুটিকে শ্রেণি সমবায়ে যুক্ত করলে প্রতিটি বাতির মধ্য দিয়ে একই তড়িৎপ্রবাহ \( \left(I\right) \) হবে। তাই জুলের সূত্র, \( H\propto I^2Rt \) থেকে বলা যায়, যে বাতির রোধ বেশি অর্থাৎ প্রথম বাতিটির ক্ষেত্রে উৎপন্ন তাপের পরিমাণ বেশি, তাই প্রথম বাতিটিই অধিকতর উজ্জ্বলভাবে জ্বলবে।
240 V-500 W ও 240 V-1000 W এই দুটি বৈদ্যুতিক বাতির কোনটির ফিলামেন্ট মোটা?
\( R \) রোধের কোনো বাতির দুই প্রান্তে \( V \) বিভবপ্রভেদ প্রয়োগ করলে যদি ব্যয়িত ক্ষমতা \( P \) হয় তবে
\( P=\frac{V^2}R \\\)\( R=\frac{V^2}P \) ___(1)
(1) নং সমীকরণ থেকে প্রথম বাতির রোধ, \( R_1=\frac{240^2}{500}=115.2\;\Omega \) ও দ্বিতীয় বাতির রোধ, \( R_2=\frac{240^2}{1000}=57.6\;\Omega \) । আবার কোনো পরিবাহীর দৈর্ঘ্য \( \left(l\right) \) অপরিবর্তিত থাকলে রোধ, \( R\propto\frac1A \), যেখানে \( A \) হল পরিবাহীর প্রস্থচ্ছেদের ক্ষেত্রফল। যেহেতু দ্বিতীয় বাতির রোধ কম তাই দ্বিতীয় বাতির ফিলামেন্টের প্রস্থচ্ছেদের ক্ষেত্রফল বেশি বা ফিলামেন্টটি প্রথমটির তুলনায় মোটা হবে।
220 V-100 W -এর একটি বাতিকে 440 V লাইনে যুক্ত করলে কী হবে? বাতিটিকে 160 V লাইনে যুক্ত করলে কী হবে?
220 V-100 W -এর একটি বাতিকে 440 V লাইনে যুক্ত করলে বাতির মধ্য দিয়ে সর্বোচ্চ প্রবাহমাত্রা অপেক্ষা বেশি তড়িৎপ্রবাহ হবে, ফলে অত্যন্ত বেশি তাপ উৎপন্ন হবে ও বাতিটি পুড়ে যাবে। তাই খুব অল্প সময়ের জন্য বাতিটি উজ্জ্বলভাবে জ্বলার পর নষ্ট হয়ে যাবে।
বাতিটিকে 160 V লাইনে যুক্ত করলে বাতির মধ্য দিয়ে তড়িৎপ্রবাহ সর্বোচ্চ মান অপেক্ষা কম হবে তাই বাতিটি কম উজ্জ্বলভাবে জ্বলবে।
কাৰ্যনীতিসহ বৈদ্যুতিক বাতির বর্ণনা দাও।
তড়িৎপ্রবাহের তাপীয় ফলের ব্যাবহারিক প্রয়োগের একটি উৎকৃষ্ট উদাহরণ হল বৈদ্যুতিক বাতি। একটি সিল করা কাচের বাল্বের মধ্যে দুটি মোটা পরিবাহী তার প্রবেশ করানো থাকে। এই

তার দুটির প্রান্তের সঙ্গে টাংস্টেন নির্মিত একটি লম্বা ফিলামেন্ট থাকে। তড়িৎপ্রবাহ পাঠালে ফিলামেন্টটি অত্যন্ত উত্তপ্ত হয় এবং ভাস্বর হয়ে আলো দেয়। টাংস্টেনের গলনাঙ্ক বেশি (3380°C) হওয়ায় উচ্চ তাপমাত্রাতেও এটি গলে যায় না। আবার এটি যাতে জারিত হতে না পারে সেইজন্য বাল্বটি বায়ুশূন্য করা হয় অথবা কোনো নিষ্ক্রিয় গ্যাস যেমন আর্গন বা কোনো কোনো ক্ষেত্রে নাইট্রোজেন গ্যাস দ্বারা পূর্ণ করা হয়। বর্তমানে ফিলামেন্টটি টাংস্টেনের পরিবর্তে উলফ্রেমাইটের (টাংস্টেন, লোহা ও ম্যাঙ্গানিজের সংকর ধাতু) তৈরি হয়।
নির্বাত বাল্ব ও গ্যাসপূর্ণ বাল্ব কী? কোনটি বেশি আলো দিতে পারে?
বায়ুশূন্য বৈদ্যুতিক বাল্বকে নির্বাত বাল্ব (vacuum bulb) ও কোনো নিষ্ক্রিয় গ্যাস বা N2 পূর্ণ বাল্বকে গ্যাসপূর্ণ বাল্ব (gas filled bulb) বলা হয়।
নির্বাত বাল্বের অপেক্ষা গ্যাসপূর্ণ বাল্বের ফিলামেন্টের উষ্ণতা বেশি বাড়ানো যায়, তাই গ্যাসপূর্ণ বাল্ব বেশি আলো দিতে পারে।
বৈদ্যুতিক বাতির ফিলামেন্ট টাংস্টেনের তৈরি হয় কেন?
টাংস্টেনের গলনাঙ্ক (3380°C) বেশি হওয়ায় উচ্চ তাপমাত্রাতেও এটি গলে না। এছাড়া টাংস্টেনের রোধাঙ্কও বেশি হওয়ায়, তারের রোধ বেশি হয় এবং তড়িৎপ্রবাহে অত্যন্ত উত্তপ্ত হয়ে আলো বিকিরণ করে। আবার টাংস্টেন ধাতু দিয়ে সরু ও লম্বা তার তৈরি করা যায়। এইসব কারণে বৈদ্যুতিক বাতির ফিলামেন্ট টাংস্টেনের তৈরি হয়।
বৈদ্যুতিক বাল্ব বায়ুশূন্য বা বায়ুপূর্ণ না করে নিষ্ক্রিয় গ্যাস বা নাইট্রোজেন পূর্ণ করা হয় কেন?
কোনো বৈদ্যুতিক বাল্ব বায়ুশূন্য করলে ফিলামেন্টটি উচ্চ তাপমাত্রায় বাষ্পীভূত হয়, তাই কিছুদিন পরে ফিলামেন্টটি ক্ষয়প্রাপ্ত হয়ে ফেটে যায় এবং বাষ্পীভূত হয়ে বাল্বের ভিতরের দেয়ালে একটি আস্তরণ তৈরি করে। এর ফলে কাচের স্বচ্ছতা কমে যায় এবং বাল্বের উজ্জ্বলতা হ্রাস পায়। আবার বাল্বটি বায়ুপূর্ণ করা হলে উচ্চ তাপমাত্রায় বায়ুর অক্সিজেন দ্বারা ফিলামেন্টটি জারিত হয়ে ধাতব অক্সাইড উৎপন্ন করে এবং বাল্বের কর্মক্ষমতা হ্রাস পায়। এইসব কারণে বৈদ্যুতিক বাল্বে নিষ্ক্রিয় গ্যাস বা নাইট্রোজেন গ্যাস পূর্ণ করা হয়। ফলে ফিলামেন্টের জারিত হবার সম্ভাবনা থাকে না এবং বাষ্পীভবন খুব কম হওয়ার জন্য বাল্ব বেশি দিন চলে।
বৈদ্যুতিক বাল্বে যে দুটি মোটা পরিবাহী তারের প্রান্তে ফিলামেন্টটি যুক্ত করা থাকে সেই তারে একই তড়িৎপ্রবাহ যাওয়া সত্ত্বেও আলো বিকিরণ করে না কেন?
বৈদ্যুতিক বাল্বে যে দুটি মোটা পরিবাহী তারের প্রান্তে ফিলামেন্টটি যুক্ত থাকে সেই তার দুটির দৈর্ঘ্য কম এবং প্রস্থচ্ছেদের ক্ষেত্রফল বেশি হওয়ায় রোধ কম হয়। রোধ কম হওয়ার জন্য একই তড়িৎপ্রবাহ যাওয়া সত্ত্বেও তার দুটি কম উত্তপ্ত হয়, তাই আলো বিকিরণ করে না।
কার্যনীতিসহ বৈদ্যুতিক হিটারের বর্ণনা দাও।
বৈদ্যুতিক হিটারে একটি ধাতব পাত্রের মধ্যে তড়িতের কুপরিবাহী পদার্থ, যেমন অভ্র বা ফায়ার ক্লে নির্মিত একটি খাঁজকাটা গোল চাকতি থাকে। ওই খাঁজের মধ্যে নাইক্রোম (Ni, Cr ও Fe -এর সংকর ধাতু) নির্মিত একটি লম্বা তারকে স্প্রিং -এর মতো পেঁচিয়ে বসানো হয়। নাইক্রোম তারের দুই প্রান্ত প্লাগের সাহায্যে বৈদ্যুতিক লাইনে যুক্ত করলে নাইক্রোম তারের কুণ্ডলীটি উত্তপ্ত হয়ে লাল হয়ে যায়। নাইক্রোমের রোধাঙ্ক বেশি, তাই বেশি উত্তপ্ত হয় এবং এটি সহজে জারিত হয় না। এছাড়া নাইক্রোমের গলনাঙ্ক বেশি, তাই এইসব কারণে হিটারে নাইক্রোম তার ব্যবহৃত হয়। ফায়ার ক্লে বা অভ্রের চাকতির ওপর তাপ সহনশীল পদার্থ যেমন পোর্সেলিনের পাটাতন থাকে যার ওপর রান্নার সামগ্রী রাখা হয়, ফলে রান্নার সামগ্রীর সঙ্গে তড়িৎ সংযোগ ঘটার সম্ভাবনা থাকে না।

একটি বৈদ্যুতিক হিটারে যদিও অনবরত তাপ উৎপন্ন হয়, কিন্তু হিটারটি জ্বালানোর কিছুক্ষণ পরেই তার উষ্ণতা স্থির হয়ে যায়। এর কারণ কী?
একটি বৈদ্যুতিক হিটারে তড়িৎপ্রবাহ পাঠালে হিটারের কুণ্ডলীতে জুলের সূত্রানুযায়ী তাপ উৎপন্ন হয় এবং কুণ্ডলীর তাপমাত্রা বৃদ্ধি পায়, ফলে পারিপার্শ্বিকের সঙ্গে হিটারের কুণ্ডলীর তাপমাত্রার পার্থক্য বাড়তে থাকে। এই উষ্ণতার পার্থক্য যত বেশি হয় কুণ্ডলীর তাপ বিকিরণের হারও তত বেশি হয়। এইভাবে তাপমাত্রা বাড়তে বাড়তে কুণ্ডলীর তাপমাত্রা এমন হয় যে, কুণ্ডলীতে যে হারে তাপ উৎপন্ন হয়, কুণ্ডলী সেই হারে তাপ বিকিরণ করে। এই অবস্থায় কুণ্ডলীর তাপমাত্রা আর বাড়ে না, একটি নির্দিষ্ট মানে স্থির হয়ে যায়।
বৈদ্যুতিক হিটারে নাইক্রোম তার ব্যবহার করা হয় কেন?
নাইক্রোম হল নিকেল, ক্রোমিয়াম ও লোহার সংকর ধাতু। নাইক্রোমের রোধাঙ্ক বেশি তাই বেশি উত্তপ্ত হয় এবং গলনাঙ্ক (প্রায় 1400°C) বেশি তাই উত্তপ্ত অবস্থাতে এটি সহজে গলে যায় না। তাছাড়া উচ্চ তাপমাত্রাতেও এটি সহজে জারিত হয় না। এইসব কারণে হিটারে নাইক্রোম তার ব্যবহার করা হয়।
হিটারে যে নাইক্রোম তারের কুণ্ডলী আছে তার দৈর্ঘ্য একটু কেটে দিলে কী হবে?
নাইক্রোম তারের দৈর্ঘ্য কমালে কুণ্ডলীর রোধ কম হয়। আমরা জানি, বাড়িতে বিভিন্ন বৈদ্যুতিক যন্ত্র সমান্তরাল সমবায়ে থাকে এবং সমান্তরাল সমবায়ে থাকার জন্য বিভিন্ন তড়িৎযন্ত্রের দুই প্রান্তের বিভবপ্রভেদ স্থির থাকে। এক্ষেত্রে উৎপন্ন তাপ রোধের ব্যস্তানুপাতিক হয় \( (H=\frac{V^2}{R^2}Rt \) বা, \( H\propto\frac1R) \) তাই বেশি তাপ উৎপন্ন হয়। সুতরাং হিটারে যে নাইক্রোম তারের কুণ্ডলী আছে তার দৈর্ঘ্য একটু কেটে দিলে পূর্বাপেক্ষা বেশি তাপ উৎপন্ন হবে।
কার্যনীতিসহ বৈদ্যুতিক ইস্ত্রির বর্ণনা দাও।
বৈদ্যুতিক ইস্ত্রিতে একটি নাইক্রোম তারের কুণ্ডলীকে ত্রিভুজাকৃতি দুটি অভ্রের পাতের মধ্যে লাগানো থাকে। এটিকে লোহার আবরণের মধ্যে ভালোভাবে রাখা হয়। কুণ্ডলীর মধ্য দিয়ে তড়িৎপ্রবাহ পাঠালে সেটি উত্তপ্ত হয় তাই লোহার আবরণটিও উত্তপ্ত হয়ে ওঠে এবং এর সাহায্যে জামাকাপড় ইস্ত্রি করা যায়। লোহার আবরণের তলদেশ মসৃণ করা হয়। নাইক্রোম তারের কুণ্ডলীটি অভ্রের পাত দ্বারা ঢাকা থাকে বলে শক লাগার সম্ভাবনা থাকে না। তবে অভ্রের পাত ছিদ্রযুক্ত হলে সেই ইস্ত্রি থেকে শক লাগতে পারে। জামাকাপড় ইস্ত্রি করার সময় যাতে হাতে তাপ না লাগে সেইজন্য ইস্ত্রির হাতল কুপরিবাহী পদার্থের তৈরি হয়।

ইলেকট্রিক ফিউজ কী? ফিউজ তার কী? ইলেকট্রিক ফিউজের কার্যনীতি লেখো।
ইলেকট্রিক ফিউজ হল এমন একটি ব্যবস্থা যেটিকে তড়িৎবর্তনীতে শ্রেণি সমবায়ে যুক্ত করা হয় এবং যা অতিরিক্ত প্রবাহের জন্য বর্তনীকে ক্ষতিগ্রস্ত হওয়া থেকে রক্ষা করে।
ফিউজ তার হল টিন ও সিসার সংকর ধাতুর (টিন 75%, সিসা 25%) তৈরি এক ধরনের কম গলনাঙ্ক বিশিষ্ট তার। একটি চিনামাটির হোল্ডারে তারটিকে যুক্ত করে বৈদ্যুতিক লাইনের সঙ্গে লাগানো হয়।
ইলেকট্রিক ফিউজকে বৈদ্যুতিক লাইনের লাইভ তারের সঙ্গে শ্রেণি সমবায়ে যুক্ত করা হয়। ফিউজ তারের গলনাঙ্ক ও রোধাঙ্ক কম। প্রতিটি ফিউজ তার একটি সর্বোচ্চ তড়িৎপ্রবাহ বহন করতে পারে। কোনো কারণে বৈদ্যুতিক লাইনে তড়িৎপ্রবাহ হঠাৎ বেড়ে গেলে তারটি গলে গিয়ে বর্তনীকে বিচ্ছিন্ন করে দেয় এবং বিপদ থেকে রক্ষা করে।
10 A ফিউজ বলতে কী বোঝ?
10 A ফিউজ বলতে বোঝায় ওই ফিউজ তারের সর্বোচ্চ প্রবাহমাত্রা 10 A। ওই তারে তড়িৎপ্রবাহ 10 A অপেক্ষা বেশি হলে তারটি উত্তপ্ত হয়ে গলে যাবে এবং বর্তনীকে বিচ্ছিন্ন করে দেবে। এর ফলে বর্তনীতে তড়িৎপ্রবাহ বন্ধ হয়ে যাবে।
ফিউজ তারে সর্বোচ্চ তড়িৎপ্রবাহ ব্যাসার্ধের মধ্যে সম্পর্কটি লিখো।
প্রতিটি ফিউজ তার একটি নির্দিষ্ট মানের তড়িৎপ্রবাহ সহ্য করতে পারে। ফিউজ তারে সর্বোচ্চ তড়িৎপ্রবাহ \( I \) ও ব্যাসার্ধ \( r \) হলে, \( I^2\propto r^3 \)।
ভাস্বর ল্যাম্প, CFL ও LED -এর মধ্যে শক্তি সাশ্রয়ের সাপেক্ষে তুলনামূলক আলোচনা করো।
ভাস্বর ল্যাম্পে ব্যয়িত তড়িৎশক্তির প্রায় 98% তাপশক্তিতে রূপান্তরিত হয় এবং প্রায় 2% দৃশ্যমান আলো উৎপন্ন করে। CFL (Compact Fluorescent Lamps) ব্যয়িত তড়িৎশক্তির 7% থেকে 9% দৃশ্যমান আলো উৎপন্ন করে এবং LED (Light Emitting Diode) ব্যয়িত তড়িৎশক্তির প্রায় 4% থেকে 18% দৃশ্যমান আলো উৎপন্ন করে। তাই ভাস্বর ল্যাম্প শক্তি সাশ্রয়কারী নয়। এর চেয়ে CFL ও LED বেশি শক্তি সাশ্রয়কারী। ভাস্বর ল্যাম্পের তুলনায় CFL ও LED -এর দাম বেশি হলেও এগুলি অনেক তড়িৎশক্তি সাশ্রয় করে খরচ কমায়।

CFL ও LED -এর মধ্যে পার্থক্য কী?
CFL ও LED -এর মধ্যে পার্থক্য –
- LED বাল্বের দাম CFL -এর তুলনায় বেশি।
- LED অর্ধপরিবাহী দ্বারা তৈরি করা হয়, কিন্তু CFL তৈরিতে পারদ ব্যবহার করা হয়। ভেঙে যাওয়া CFL খুবই বিপজ্জনক, কারণ পারদ স্বাস্থ্যের পক্ষে ক্ষতিকারক।
- LED বাল্বের আয়ুষ্কাল CFL -এর তুলনায় বেশি।
- LED বাল্ব CFL -এর তুলনায় বেশি শক্তি সাশ্রয়কারী।
ভাস্বর ল্যাম্প, CFL ও LED -এর কোনটির জীবনকাল কত?
একটি ভাস্বর ল্যাম্পের CFL ও LED -এর জীবনকাল যথাক্রমে প্রায় 1000 h, প্রায় 10000 h ও প্রায় 30000 h।
একই উপাদানের ও একই দৈর্ঘ্যের একটি সরু ও একটি মোটা তারের মধ্য দিয়ে একই তড়িৎপ্রবাহ একই সময় ধরে পাঠানো হলে কোনটি বেশি উত্তপ্ত হবে?
একই উপাদান ও একই দৈর্ঘ্যের সরু তারের রোধ মোটা তারের তুলনায় বেশি, তাই একই সময় ধরে একই তড়িৎপ্রবাহ পাঠানো হলে সরু তারটি বেশি উত্তপ্ত হবে।
একই উপাদান ও একই প্রস্থচ্ছেদের ক্ষেত্রফলযুক্ত দুটির তারের প্রথমটির দৈর্ঘ্য, দ্বিতীয়টির তুলনায় বেশি। উভয় তারের মধ্য দিয়ে একই সময় ধরে একই তড়িৎপ্রবাহ পাঠানো হলে কোনটি বেশি উত্তপ্ত হবে?
একই উপাদান ও একই প্রস্থচ্ছেদের ক্ষেত্রফলবিশিষ্ট দুটি তারের যেটির দৈর্ঘ্য বেশি তার রোধ বেশি হবে। অর্থাৎ প্রথম তারটির রোধ দ্বিতীয় তারটির অপেক্ষা বেশি হবে। তাই উভয় তারের মধ্য দিয়ে একই সময় ধরে একই তড়িৎপ্রবাহ পাঠানো হলে প্রথম তারটি বেশি উত্তপ্ত হবে।
বৈদ্যুতিক বাতির ফিলামেন্ট আলো বিকিরণ করে কিন্তু হিটারের কুণ্ডলী আলো বিকিরণ করে না কেন?
বৈদ্যুতিক বাতির ফিলামেন্ট টাংস্টেনের তৈরি। এটি খুব সরু। আবার হিটারের কুণ্ডলী নাইক্রোমের তৈরি, এটির প্রস্থচ্ছেদের ক্ষেত্রফল বেশি অর্থাৎ ফিলামেন্টের তুলনায় মোটা। ফলে বাতির ফিলামেন্টের রোধ তুলনামূলকভাবে বেশি। রোধ বেশি হওয়ার জন্য ফিলামেন্ট বেশি উত্তপ্ত হয় ও শ্বেততপ্ত হয়ে আলো বিকিরণ করে। কিন্তু হিটারের কুণ্ডলীর রোধ কম হওয়ায় সেইভাবে উত্তপ্ত হয় না, তাই শ্বেততপ্ত হয়ে আলো বিকিরণ করে না।
তড়িৎপ্রবাহের চৌম্বক ক্রিয়া
তড়িৎপ্রবাহের চৌম্বক ক্রিয়া দেখানোর জন্য ওরস্টেডের পরীক্ষাটি বর্ণনা করো।
অথবা, একটি সহজ পরীক্ষার দ্বারা তড়িৎপ্রবাহের চৌম্বক ক্রিয়া দেখাও।
বিজ্ঞানী ওরস্টেড 1820 খ্রিস্টাব্দে তড়িৎপ্রবাহের চৌম্বক ক্রিয়া দেখানোর জন্য একটি পরীক্ষা করেন। সেই পরীক্ষা অনুযায়ী নিম্নলিখিত পরীক্ষাটি করা হল।
উপকরণ – 1.5 V -এর দুটি ব্যাটারি, একটি মোটা তামার তার, সংযোগকারী তার, টোস্টার, সুইচ, চুম্বক শলাকা, রোধক তার।
পরীক্ষা – ব্যাটারি দুটিকে টোস্টারে লাগিয়ে, মোটা তামার তার, রোধক তার (R) ও সুইচকে সংযোগকারী তার দিয়ে সংযোগ স্থাপন করে একটি টেবিলের ধার ঘেঁষে রাখা হল, যেখানে AB হল মোটা তামার তার। এবার AB তারটিকে টেবিলের বাইরে স্থাপন করা হল যাতে AB তার পড়ে না যায় বা হেলে না যায়। AB তারকে এমনভাবে রাখা হল যাতে A দক্ষিণ দিকে ও B উত্তর দিকে থাকে। সুইচ অফ করে চুম্বক শলাকাকে AB তারের নীচে রাখা হল। এই অবস্থায় চুম্বক শলাকা উত্তর-দক্ষিণ দিক বরাবর মুখ করে থাকে। এবার সুইচ অন করলে দেখা যাবে চুম্বক শলাকার উত্তর মেরু পশ্চিম দিকে বিক্ষিপ্ত হল। সুইচ অফ করে চুম্বক শলাকাকে AB তারের ওপরে ধরে, সুইচ অন করে দেখা গেল চুম্বক শলাকার উত্তর মেরু পূর্ব দিকে বিক্ষিপ্ত হল।
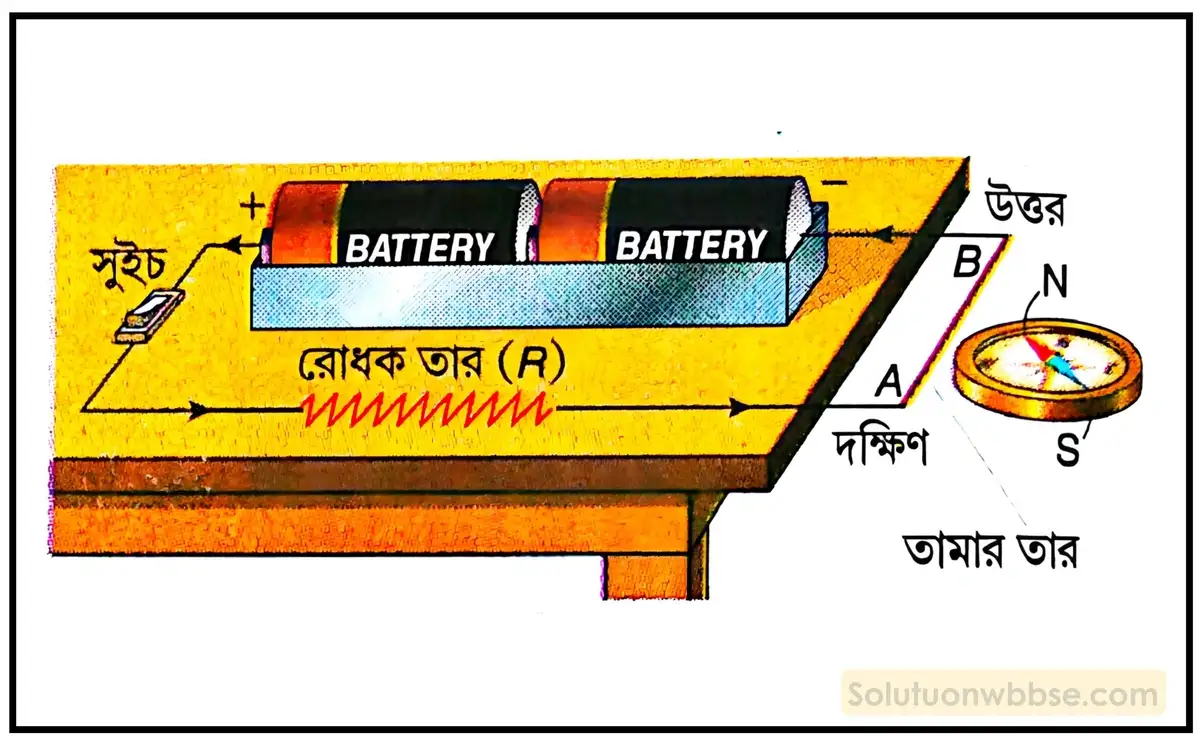
এবার ব্যাটারির মেরু দুটি উলটে দেওয়া হল, ফলে AB তারে তড়িৎপ্রবাহ B থেকে A -এর দিকে বা উত্তর থেকে দক্ষিণ দিকে হয়। পূর্বের মতো চুম্বক শলাকাকে AB তারের নীচে ও ওপরে রাখা হলে দেখা যায় চুম্বক শলাকার উত্তর মেরু যথাক্রমে পূর্ব দিকে ও পশ্চিম দিকে বিক্ষিপ্ত হয়।
সিদ্ধান্ত – ওরস্টেডের এই পরীক্ষা থেকে এই সিদ্ধান্তে আসা যায় যে, কোনো তড়িদবাহী তারের চারপাশে একটি চৌম্বক ক্ষেত্র উৎপন্ন হয় এবং তড়িৎপ্রবাহের অভিমুখ বিপরীত করলে চৌম্বক ক্ষেত্রের অভিমুখও বিপরীত দিকে হয়।
ওরস্টেডের পরীক্ষার সাহায্যে বোঝা যায় একটি পরিবাহী তারের মধ্য দিয়ে তড়িৎপ্রবাহ চালনা করলে তারটির চারপাশে চৌম্বক ক্ষেত্র উৎপন্ন হয়। কিন্তু তারটি কি চুম্বকিত হয়?
না, এক্ষেত্রে তারটি চুম্বকিত হবে না। তড়িদবাহী তারের সংস্পর্শে একটি কাগজে কিছু লৌহচূর্ণ রেখে নিয়ে গেলে দেখা যাবে লৌহচূর্ণগুলো তার দ্বারা আকর্ষিত হচ্ছে না।
চৌম্বক ক্ষেত্রের অভিমুখ কী? কীভাবে চৌম্বক ক্ষেত্রের দিক নির্ণয় করা হয়?
চৌম্বক ক্ষেত্রে একটি ক্ষুদ্র বিচ্ছিন্ন উত্তর মেরু স্থাপন করলে উত্তর মেরুর ওপর চৌম্বক ক্ষেত্র যে দিকে বল প্রয়োগ করে সেটিই হল চৌম্বক ক্ষেত্রের অভিমুখ।
বিচ্ছিন্ন চৌম্বক মেরু পাওয়া সম্ভব নয়, তাই চৌম্বক ক্ষেত্রের অভিমুখ নির্ণয়ের জন্য চুম্বক শলাকা ব্যবহার করে তার উত্তর মেরুর বিক্ষেপ নেওয়া হয়।
অ্যাম্পিয়ারের সন্তরণ নিয়মটি লেখো।
অ্যাম্পিয়ারের সন্তরণ নিয়ম – তড়িদবাহী তার বরাবর কোনো ব্যক্তি চুম্বক শলাকার দিকে মুখ করে তড়িৎপ্রবাহের অভিমুখে সাঁতার কাটতে থাকলে, ব্যক্তিটির প্রসারিত বাম হাতটি যেদিকে থাকবে চুম্বক শলাকার উত্তর মেরু সেইদিকে বিক্ষিপ্ত হবে, অর্থাৎ চৌম্বক ক্ষেত্রের দিক নির্দেশ করবে।
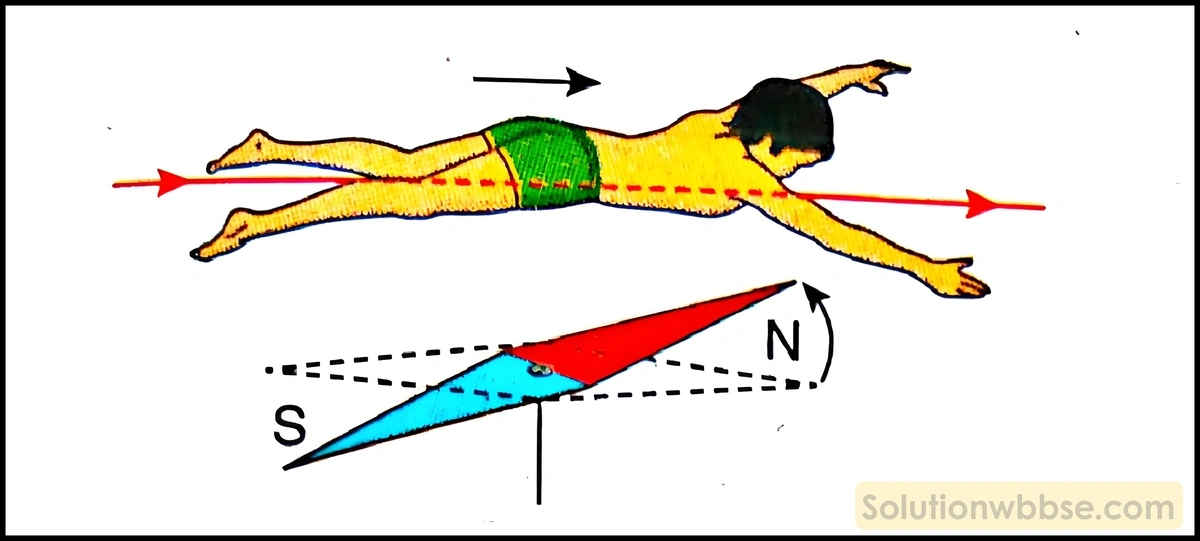
ওরস্টেডের পরীক্ষার সাহায্যে অ্যাম্পিয়ারের সন্তরণ নিয়মটি ব্যাখ্যা করো।
মনে করি, কোনো ব্যক্তি দক্ষিণ থেকে উত্তর দিকে সাঁতার কাটছে অর্থাৎ তড়িদবাহী তারে প্রবাহমাত্রা দক্ষিণ থেকে উত্তর দিকে চলছে। ওরস্টেডের পরীক্ষা থেকে পাওয়া যায়, তড়িদবাহী তারের মধ্য দিয়ে প্রবাহমাত্রা দক্ষিণ থেকে উত্তরে হলে তারের নীচে থাকা চুম্বক শলাকার উত্তর মেরুর বিক্ষেপ পশ্চিম দিকে হয়। ব্যক্তি দক্ষিণ থেকে উত্তর দিকে সাঁতার কাটলে তাঁর প্রসারিত বাম হাত থাকে পশ্চিম দিকে, অর্থাৎ তড়িদবাহী তার বরাবর কোনো ব্যক্তি চুম্বক শলাকার দিকে মুখ করে সাঁতার কাটতে থাকলে ব্যক্তির প্রসারিত বাম হাতের দিকে চুম্বক শলাকার উত্তর মেরুর বিক্ষেপ হয় – এটিই হল অ্যাম্পিয়ারের সন্তরণ নিয়ম।
চৌম্বক বলরেখা কাকে বলে? চিত্রের সাহায্যে বলরেখা থেকে চৌম্বক ক্ষেত্রের অভিমুখ দেখাও।
চৌম্বক ক্ষেত্রে একটি সর্ববাধামুক্ত ও বিচ্ছিন্ন উত্তর মেরু যে পথে গমন করে, তাকে চৌম্বক বলরেখা বলা হয়। চৌম্বক বলরেখা হল কতকগুলি কল্পিত রেখা, যে রেখার যে-কোনো বিন্দুতে অঙ্কিত স্পর্শক ওই বিন্দুতে চৌম্বক ক্ষেত্রের অভিমুখ নির্দেশ করে।
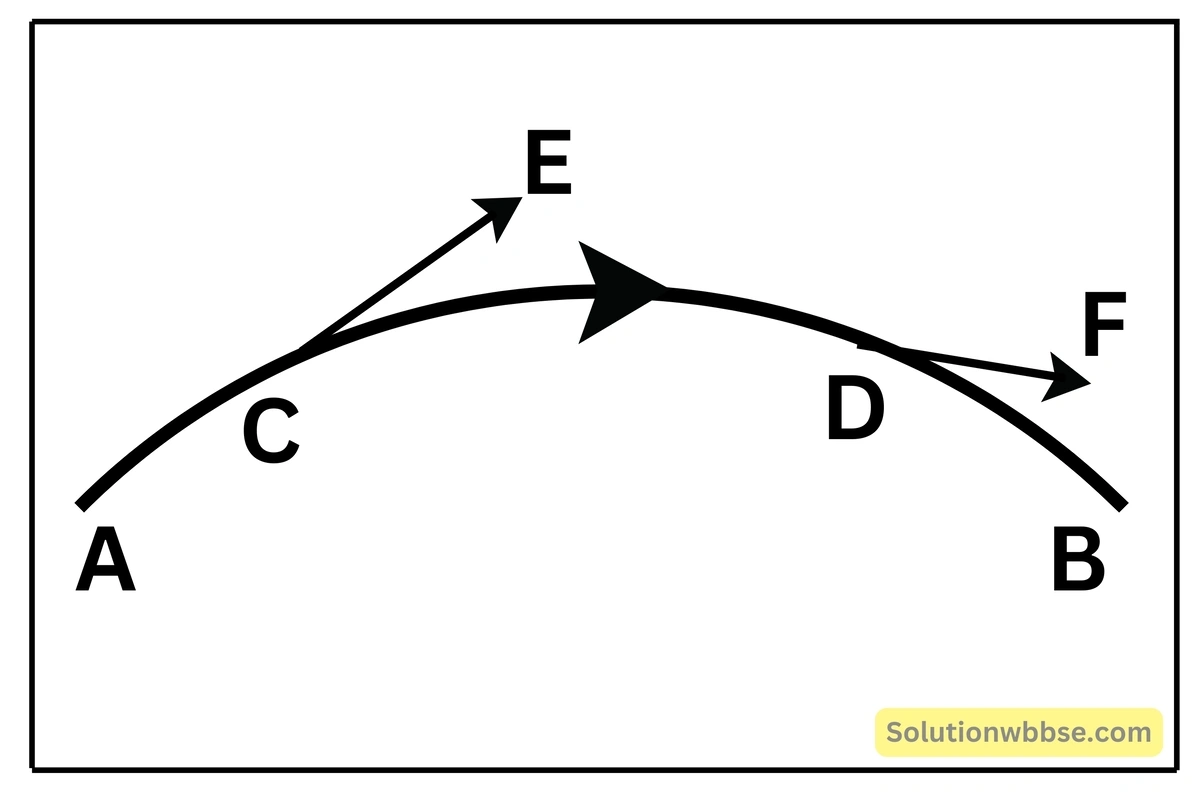
চিত্রে AB হল একটি চৌম্বক বলরেখা। AB বলরেখার ওপর C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি হল যথাক্রমে CE ও DF। তাই C ও D বিন্দুতে চৌম্বক ক্ষেত্রের অভিমুখ হল যথাক্রমে CE ও DF বরাবর।
দক্ষিণ মুষ্টি নিয়মটি লেখো এবং ওরস্টেডের পরীক্ষার সাহায্যে ব্যাখ্যা করো।
দক্ষিণ মুষ্টি নিয়ম – কোনো তড়িদবাহী তারকে ডান হাতের মুষ্টিতে ধরে বৃদ্ধাঙ্গুষ্ঠ বরাবর তড়িৎপ্রবাহ দেখানো হলে বাকি আঙুলগুলি চৌম্বক বলরেখার অভিমুখ নির্দেশ করবে।

ওরস্টেডের পরীক্ষার সাহায্যে দক্ষিণ মুষ্টি নিয়মের ব্যাখ্যা – ধরা যাক, মুষ্টিবদ্ধ ডান হাতের বৃদ্ধাঙ্গুষ্ঠটি উত্তর দিক বরাবর মুখ করে রাখা আছে। বৃদ্ধাঙ্গুষ্ঠ বরাবর তড়িৎপ্রবাহ হলে তড়িৎপ্রবাহ হয় দক্ষিণ থেকে উত্তরদিক বরাবর। এবার হাতের তর্জনী একটু খোলা হলে দেখা যাবে তর্জনী পশ্চিম দিক বরাবর মুখ করে আছে, অর্থাৎ যদি তারের নীচে কোনো চুম্বক শলাকা রাখা হয় তাহলে চুম্বক শলাকার উত্তর মেরু পশ্চিম দিকে বিক্ষিপ্ত হবে। সুতরাং ডান হাতের বৃদ্ধাঙ্গুষ্ঠ তড়িৎপ্রবাহের দিক নির্দেশ করলে বাকি আঙুলগুলি চৌম্বক বলরেখার অভিমুখ নির্দেশ করবে – এটিই হল দক্ষিণ মুষ্টি নিয়ম।
একটি লম্বা ও সোজা পরিবাহীর মধ্য দিয়ে তড়িৎপ্রবাহ পাঠালে তার চারপাশে উৎপন্ন চৌম্বক ক্ষেত্রের বলরেখা লৌহচূর্ণের সাহায্যে কীভাবে প্রদর্শন করা যায় তা ব্যাখ্যা করো।
একটি লম্বা ও সোজা পরিবাহী তার নেওয়া হল। তারটিকে একটি অনুভূমিক কার্ডবোর্ডের মধ্য দিয়ে এমনভাবে প্রবেশ করানো হল যাতে তারটি উল্লম্ব থাকে। এবার তারটির সঙ্গে একটি সুইচ ও একটি তড়িৎকোশ যুক্ত করা হল। কার্ডবোর্ডের ওপর কিছু লৌহচূর্ণ ছড়িয়ে দেওয়া হল। এবার সুইচ অন করে কার্ডবোর্ডটিকে ধীরে ধীরে টোকা দেওয়া হলে দেখা যাবে লৌহচূর্ণগুলো ছেদযুক্ত রেখার মতো সজ্জিত হয়েছে। এগুলি চৌম্বক বলরেখা সূচিত করে। চৌম্বক বলরেখার অভিমুখ বোঝার জন্য একটি চুম্বক শলাকাকে বলরেখার ওপর বসানো হল। চুম্বক শলাকার উত্তর মেরুর অবস্থানের দিকে তিরচিহ্ন দেওয়া হল। বলরেখাগুলি হল কতকগুলি ক্রমবর্ধমান ব্যাসার্ধের সমকেন্দ্রিক বৃত্ত।
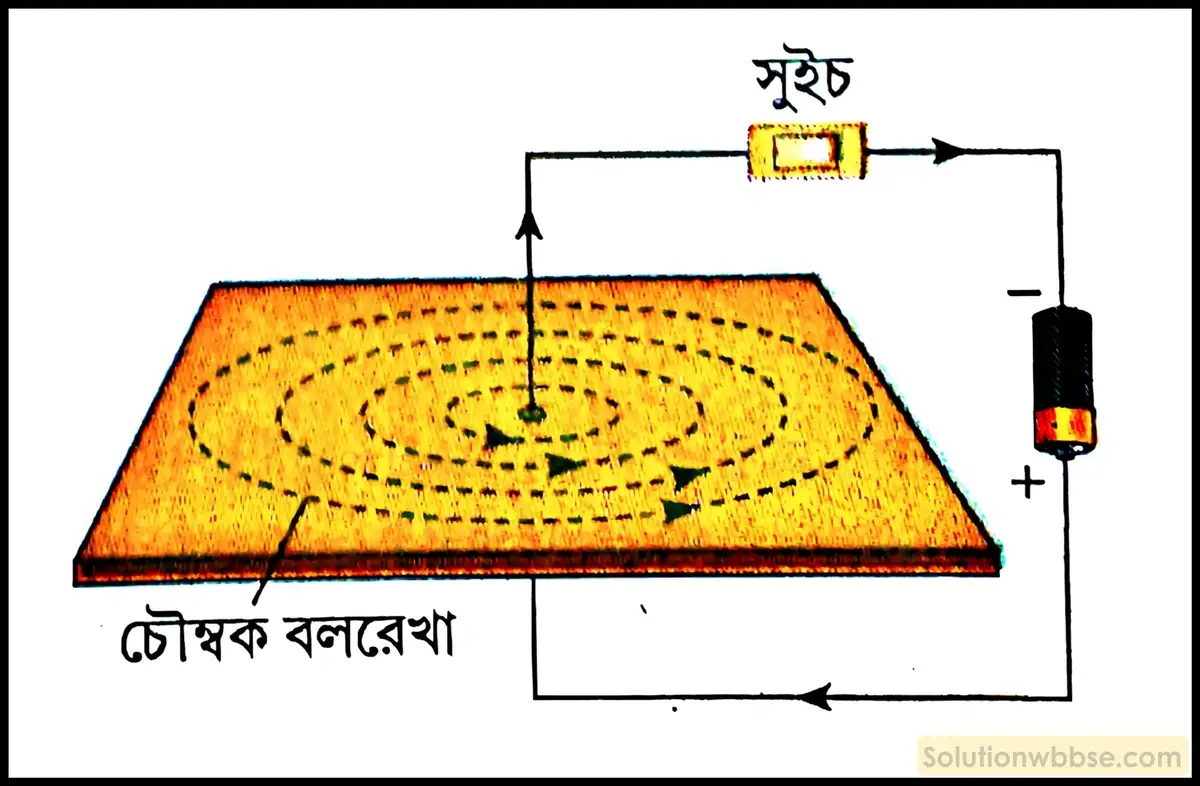
একটি স্প্রিং আকৃতির পরিবাহীর মধ্য দিয়ে তড়িৎপ্রবাহ পাঠালে তার চারপাশে উৎপন্ন চৌম্বক ক্ষেত্রের বলরেখা লৌহচূর্ণের সাহায্যে কীভাবে প্রদর্শন করা যায় তা ব্যাখ্যা করো।
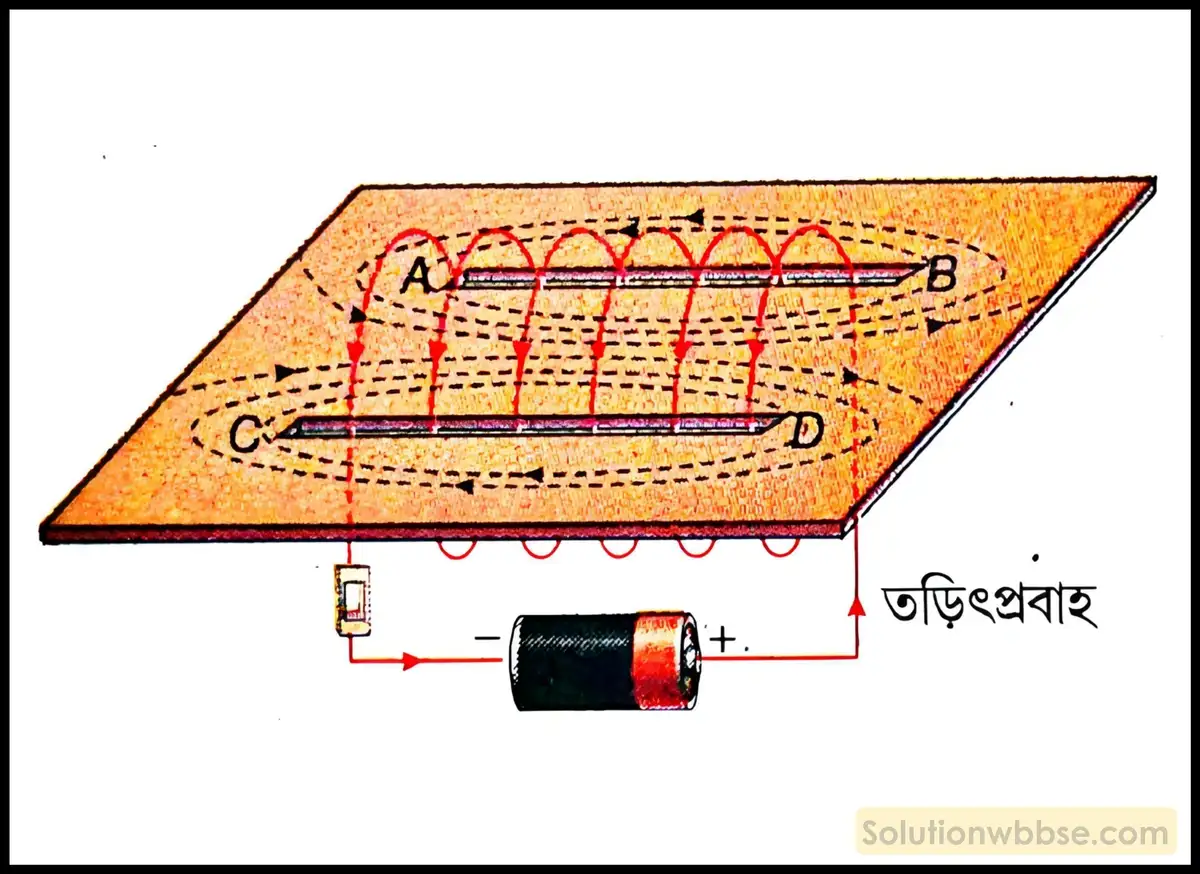
একটি কার্ডবোর্ড নেওয়া হল। কার্ডবোর্ডের ওপর AB ও CD দুটি সরলরৈখিক ছিদ্র এমনভাবে করা হল যেন AB ও CD সমান্তরাল হয়। একটি লম্বা, সোজা পরিবাহী তারকে AB -এর মধ্য দিয়ে প্রবেশ করিয়ে আবার CD -এর মধ্য দিয়ে প্রবেশ করানো হল। এইভাবে বেশ কয়েকবার করা হলে এটি স্প্রিং -এর আকৃতি হবে। এবার স্প্রিং আকৃতির পরিবাহীকে এমনভাবে বিন্যস্ত করা হল যাতে এর অক্ষ কার্ডবোর্ডের সমতলে থাকে। তারের দুই প্রান্ত একটি ব্যাটারি ও সুইচের মাধ্যমে যুক্ত করা হল। কার্ডবোর্ডের ওপর কিছু লৌহচূর্ণ ছড়িয়ে দেওয়া হল। এবার সুইচ অন করে কার্ডবোর্ডে ধীরে ধীরে টোকা দিলে দেখা যাবে লৌহচূর্ণগুলো ছেদযুক্ত রেখার মতো সজ্জিত হয়েছে। এই রেখাগুলোই চৌম্বক বলরেখা সূচিত করে। এবার চৌম্বক বলরেখার অভিমুখ নির্ণয়ের জন্য একটি চুম্বক শলাকাকে বলরেখার ওপর রাখা হল। চুম্বক শলাকার উত্তর মেরুর অবস্থানের দিকে তিরচিহ্ন দেওয়া হল। কুণ্ডলীর অভ্যন্তরে অক্ষের কাছাকাছি বলরেখাগুলি প্রায় সরলরৈখিক, মোটামুটি সমান্তরাল।
একটি দণ্ডচুম্বক ও একটি বৃত্তাকার পরিবাহীতে তড়িৎপ্রবাহের দরুণ তাদের চারপাশে উৎপন্ন চৌম্বক ক্ষেত্রের বলরেখা লৌহচূর্ণের সাহায্যে কীভাবে প্রদর্শন করা যায় তা ব্যাখ্যা করো।
একটি দণ্ডচুম্বক নেওয়া হল। দণ্ডচুম্বকটির উত্তর মেরুকে উত্তরমুখী করে কার্ডবোর্ডের ওপর স্থাপন করা হল। বেশ কিছু লৌহচূর্ণকে কার্ডবোর্ডের ওপর ছড়িয়ে দেওয়া হল। এবার কার্ডবোর্ডটিকে ধীরে ধীরে টোকা দিলে দেখা যাবে ছেদযুক্ত রেখার মতো লৌহচূর্ণগুলো সজ্জিত হয়েছে। এই
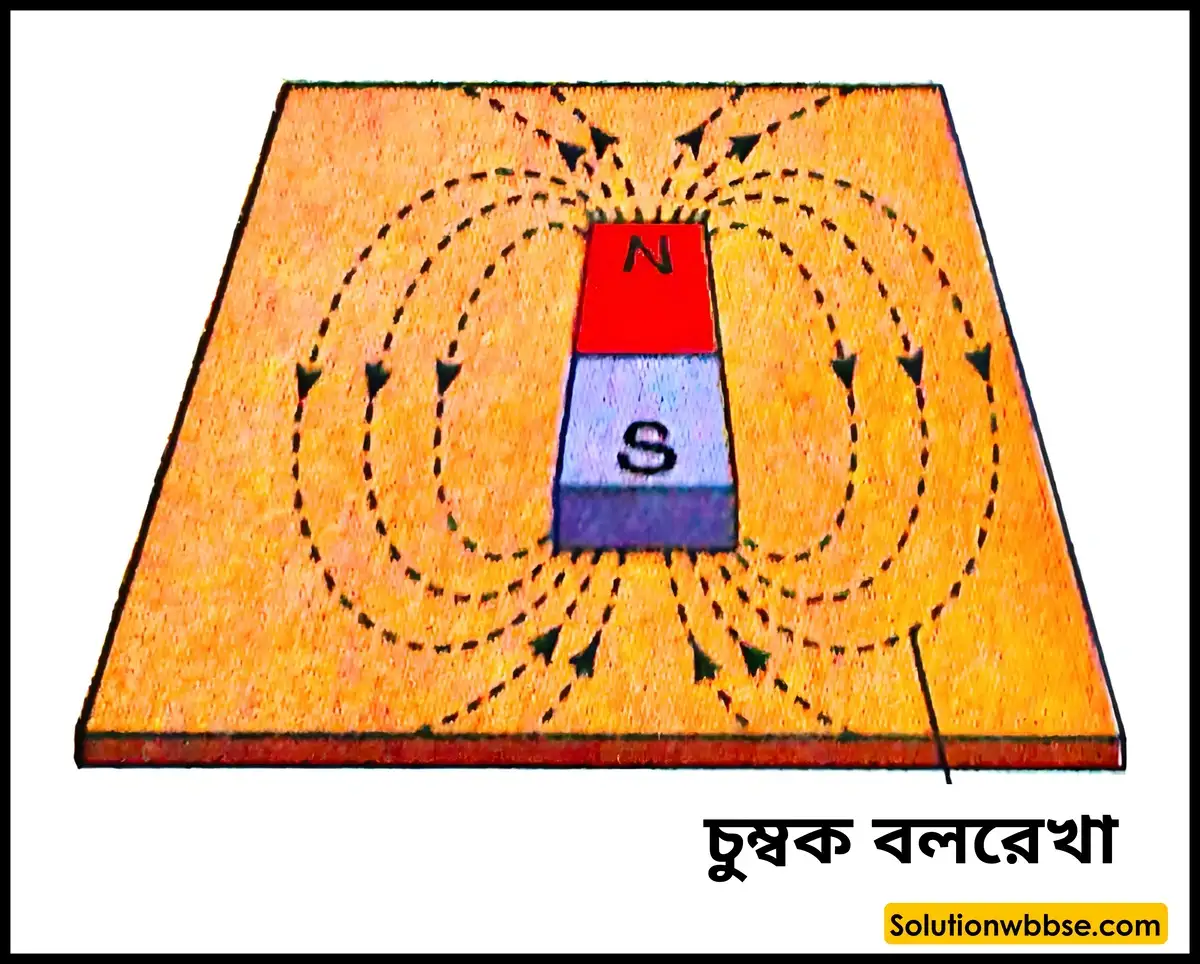
রেখাগুলি চৌম্বক বলরেখা সূচিত করে। এবার একটি চুম্বক শলাকাকে ওই রেখার ওপর রাখা হল। চুম্বক শলাকার উত্তর মেরুর অবস্থানের দিকে তিরচিহ্ন দিলে বলরেখার অভিমুখ পাওয়া যায়। এবার একটি পরিবাহী তারকে অপর একটি কার্ডবোর্ডের একটি ছিদ্রের মধ্য দিয়ে প্রবেশ করিয়ে অপর একটি ছিদ্র দিয়ে এমনভাবে বার করা হল যেন তারটি বৃত্তাকার হয়, বৃত্তাকার তারটি যে তলে অবস্থিত সেই তলের সঙ্গে কার্ডবোর্ডটি লম্বভাবে থাকে এবং বৃত্তের কেন্দ্র কার্ডবোর্ডের ওপরে থাকে। এবার তারের দুই প্রান্ত একটি ব্যাটারি ও সুইচের মাধ্যমে যুক্ত করা হল। কার্ডবোর্ডের ওপর বেশ কিছু লৌহচূর্ণ ছড়িয়ে দেওয়া হল। এবার সুইচ অন করে কার্ডবোর্ডে ধীরে ধীরে টোকা দিলে দেখা যাবে ছেদযুক্ত রেখার মতো লৌহচূর্ণগুলো সজ্জিত হয়েছে। এই রেখাগুলি চৌম্বক বলরেখা সূচিত করে। এবার একটি চুম্বক শলাকাকে ওই রেখার ওপর রাখা হল। চুম্বক শলাকার উত্তর মেরুর অবস্থানের দিকে তিরচিহ্ন দিলে বলরেখার অভিমুখ পাওয়া যায়।
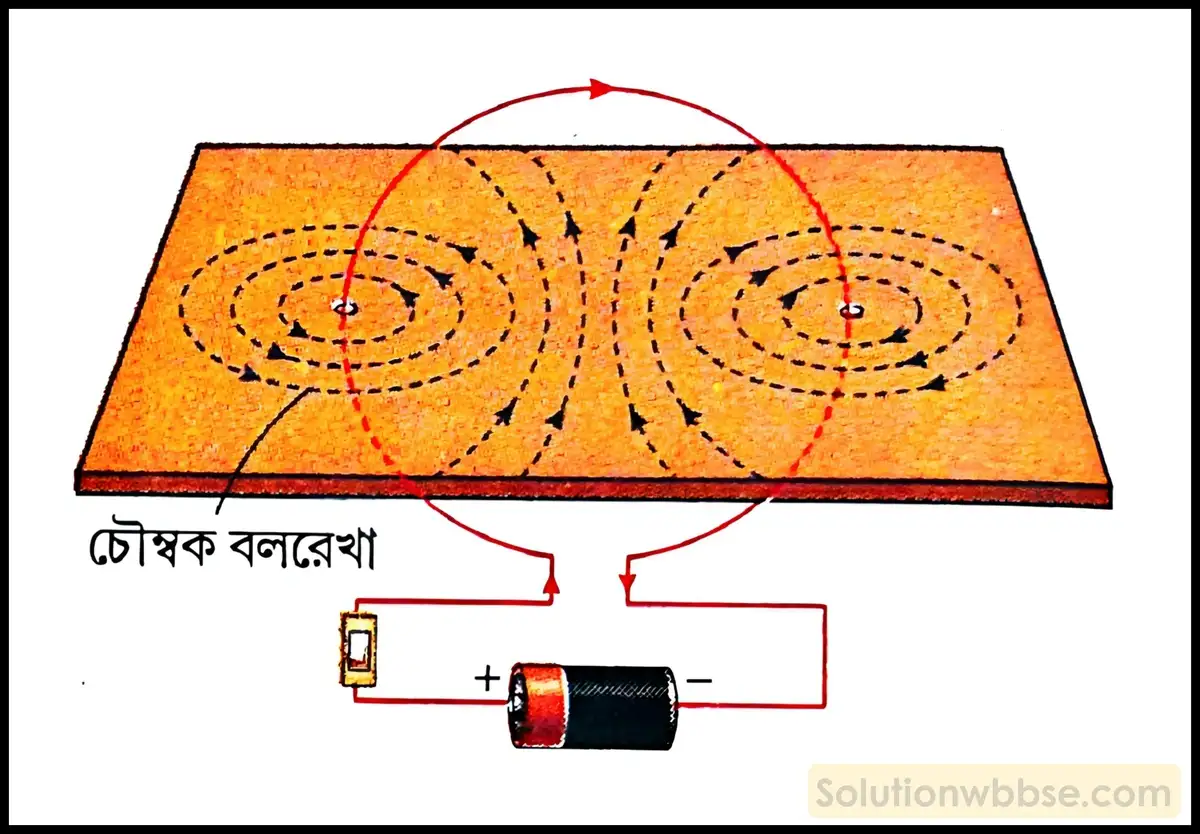
একটি দণ্ডচুম্বক এবং একটি বৃত্তাকার পরিবাহীতে তড়িৎপ্রবাহের দরুণ সৃষ্ট চৌম্বক ক্ষেত্রের মধ্যে সাদৃশ্য ব্যাখ্যা করো।
একটি দণ্ডচুম্বক ও একটি বৃত্তাকার তড়িদবাহী পরিবাহীর জন্য যে বলরেখার চিত্র পাওয়া যায় তা থেকে বোঝা যায় একটি বৃত্তাকার তড়িদবাহী পরিবাহী একটি দণ্ডচুম্বকের সমতুল্য, কারণ উভয়ক্ষেত্রে বলরেখার চিত্র অনুরূপ। বৃত্তাকার পরিবাহীতে ঘড়ির কাঁটার অভিমুখে তড়িৎপ্রবাহ হলে বৃত্তাকার পরিবাহীর সম্মুখ প্রান্ত দণ্ডচুম্বকের দক্ষিণ মেরুর মতো আচরণ করে। বিপরীত দিক থেকে দেখলে তড়িৎপ্রবাহের অভিমুখ হয় ঘড়ির কাঁটার বিপরীত অভিমুখে এবং ওই প্রান্ত উত্তর মেরুর মতো আচরণ করে।
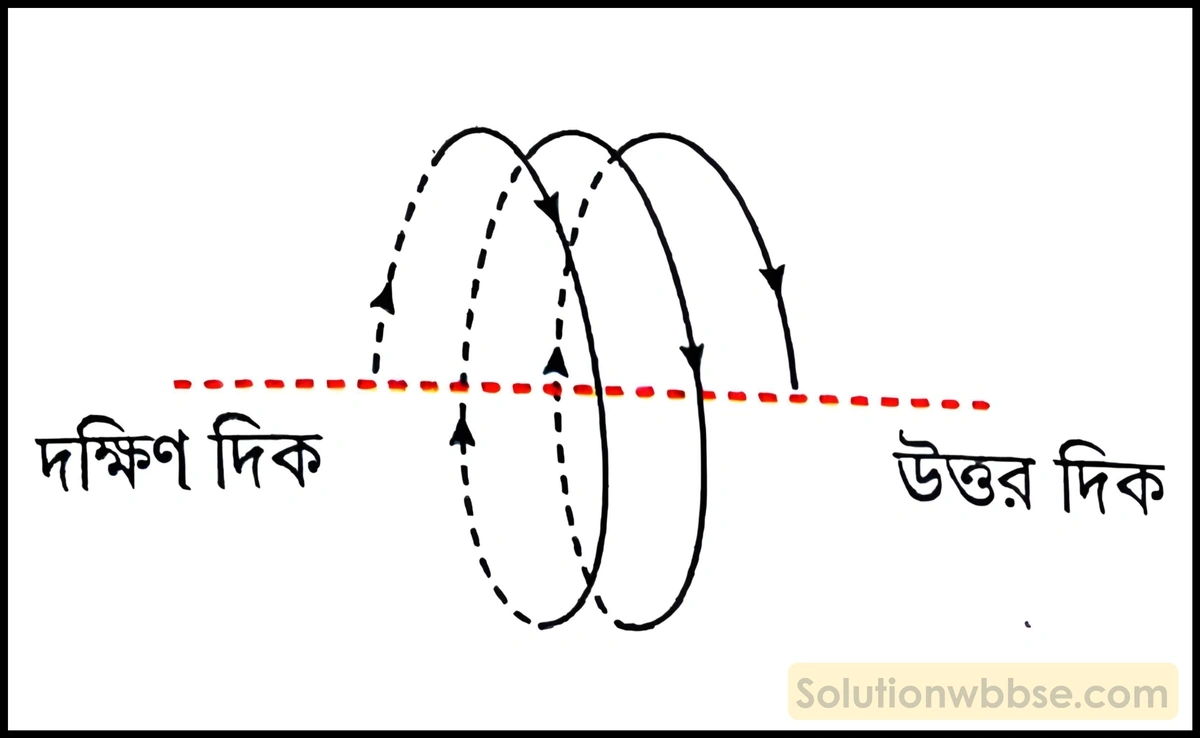
একটি তড়িদবাহী বৃত্তাকার কুণ্ডলীকে ঝুলন্ত অবস্থায় রেখে দিলে সেটি কোন্ দিক বরাবর মুখ করে থাকবে ও কেন?
একটি তড়িদবাহী বৃত্তাকার কুণ্ডলীকে ঝুলন্ত অবস্থায় রেখে দিলে সেটি এমনভাবে থাকবে যাতে এর অক্ষ উত্তর-দক্ষিণ দিক বরাবর থাকে। দক্ষিণ দিক থেকে কুণ্ডলীর দিকে তাকালে তড়িৎপ্রবাহ দক্ষিণাবর্তী এবং উত্তর দিক থেকে কুণ্ডলীর দিকে তাকালে তড়িৎপ্রবাহ বামাবর্তী হবে। এর কারণ হল বৃত্তাকার তড়িদবাহী কুণ্ডলী একটি দণ্ডচুম্বকের মতো আচরণ করে। কুণ্ডলীর যেদিক থেকে দেখলে তড়িৎপ্রবাহ দক্ষিণাবর্তী সেদিকে দক্ষিণ মেরু ও যেদিক থেকে দেখলে তড়িৎপ্রবাহ বামাবর্তী সেদিকে উত্তর মেরুর সৃষ্টি হয়। ভূ-চুম্বকত্বের জন্য এই কুণ্ডলীকে ঝুলন্ত অবস্থায় রাখলে এটির অক্ষ উত্তর-দক্ষিণ দিক বরাবর থাকে এবং উত্তর মেরু উত্তর দিকে ও দক্ষিণ মেরু দক্ষিণ দিকে থাকে।
ফ্লেমিং -এর বাম হস্ত নিয়মটি লেখো।
ফ্লেমিং -এর বাম হস্ত নিয়ম – বাম হাতের বৃদ্ধাঙ্গুষ্ঠ, তর্জনী ও মধ্যমাকে পরস্পরের সমকোণে রেখে প্রসারিত করলে যদি তর্জনী চৌম্বক ক্ষেত্রের অভিমুখ এবং মধ্যমা তড়িৎপ্রবাহের অভিমুখ নির্দেশ করে, তবে বৃদ্ধাঙ্গুষ্ঠ পরিবাহীর গতির অভিমুখ বা পরিবাহীর ওপর ক্রিয়াশীল বলের অভিমুখ নির্দেশ করবে।

চিত্রসহ বার্লোর চক্রের গঠন ও কার্যনীতি ব্যাখ্যা করো।
নীতি – বার্লোর চক্র ফ্লেমিং -এর বাম হস্ত নিয়মের ভিত্তিতে গঠিত। বার্লোর চক্রে তড়িৎশক্তি, যান্ত্রিক শক্তিতে রূপান্তরিত হয়।
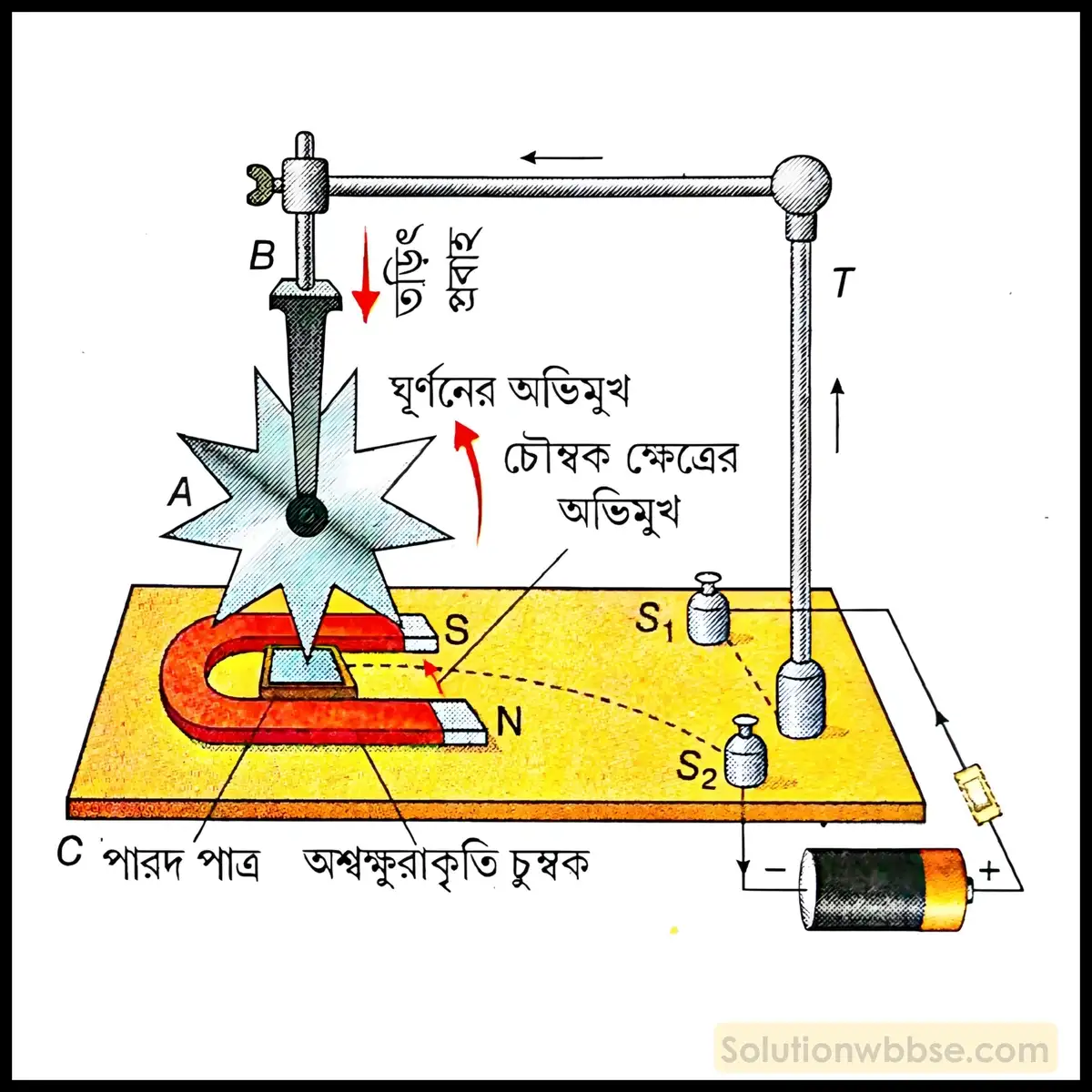
গঠন – বার্লোর চক্রের গঠন নীচের চিত্রে দেখানো হয়েছে। কয়েকটি তীক্ষ্ণ দাঁতবিশিষ্ট একটি তামার চক্র (A) -কে একটি ধাতব দণ্ডের (B) সঙ্গে এমনভাবে আটকানো থাকে যাতে চক্রটি অনুভূমিক অক্ষের সাপেক্ষে উল্লম্বতলে ঘুরতে পারে। ধাতব দণ্ডটিকে একটি স্ট্যান্ডের (T) সাহায্যে একটি কাঠের পাটাতনের (C) ওপর রাখা থাকে। চক্রের ঠিক নীচে পাটাতনের ওপর একটি গর্ত করা হয় যাতে পারদ রাখা থাকে। গর্তটি এমনভাবে করা যাতে চক্রটি ঘোরার সময় দাঁতের অগ্রভাগ পারদকে স্পর্শ করে। একটি অশ্বক্ষুরাকৃতি চুম্বক (NS) -কে এমনভাবে পাটাতনের ওপর রাখা হয় যাতে গর্তটি চুম্বকের দুই মেরুর মাঝে থাকে। পাটাতনের ওপর দুটি বন্ধনী স্ক্রু S1 ও S2 লাগানো হয়, যাতে S1 -এর সঙ্গে চক্র ও S2 -এর সঙ্গে পারদ পরিবাহী তার দ্বারা যুক্ত থাকে। S1 ও S2 স্ক্রু -এর সঙ্গে পরিবাহী তার দিয়ে একটি সুইচ ও একটি ব্যাটারি বাক্স যুক্ত করা হয়।
কার্যনীতি – সুইচ অন করলে নীচের চিত্রের মতো তড়িৎপ্রবাহ তির চিহ্নিত পথে চলতে থাকে। ফলে চক্রের মধ্য দিয়ে তড়িৎপ্রবাহ ওপর থেকে নিচের দিকে হয়। চৌম্বক ক্ষেত্রের অভিমুখ হয় কাঠের পাটাতন বরাবর উত্তর মেরু থেকে দক্ষিণ মেরুর দিকে। ফ্লেমিং -এর বাম হস্ত নিয়ম থেকে পাওয়া যায়, পারদ স্পর্শ করা চক্রের দাঁতটির ওপর চৌম্বক ক্ষেত্র বামদিক থেকে ডানদিকে বল প্রয়োগ করে। এর ফলে দাঁতটি ডানদিকে গতিশীল হয়। চক্রের দাঁত গতিশীল হলেই পারদের সঙ্গে সংযোগ বিচ্ছিন্ন হয় অর্থাৎ তড়িৎপ্রবাহ বন্ধ হয়ে যায়, কিন্তু গতিজাড্যের জন্য পরের দাঁতটি আবার পারদ স্পর্শ করে। এইভাবে যতক্ষণ তড়িৎপ্রবাহ পাঠানো হয় ততক্ষণ চক্রটি ঘুরতে থাকে।
বার্লোর চক্রে ঘূর্ণনের ক্ষেত্রে কী ঘটবে যদি
(i) তড়িৎপ্রবাহ বিপরীতমুখী হয়?
(ii) চুম্বকের মেরু দুটিকে উলটে দেওয়া হয়?
(iii) তড়িৎপ্রবাহ বিপরীতমুখী ও চুম্বকের মেরু দুটিকে উলটে দেওয়া হয়?
(iv) dc -এর পরিবর্তে ac পাঠানো হয়?
- বার্লোর চক্রে চৌম্বক ক্ষেত্রের অভিমুখ একই রেখে তড়িৎপ্রবাহ বিপরীতমুখী করলে বার্লোর চক্র বিপরীত দিকে ঘুরবে।
- বার্লোর চক্রে তড়িৎপ্রবাহের অভিমুখ একই রেখে চুম্বকের মেরু দুটিকে উলটে দিলে বার্লোর চক্র বিপরীত দিকে ঘুরবে।
- বার্লোর চক্রে তড়িৎপ্রবাহ বিপরীতমুখী ও চুম্বকের মেরু দুটিকে উলটে দিলে বার্লোর চক্র একই দিকে ঘুরবে।
- dc -এর পরিবর্তে ac পাঠালে বার্লোর চক্রের ঘূর্ণন বন্ধ হয়ে যাবে।
বার্লোর চক্রকে কি মোটর বলা যায়?
বৈদ্যুতিক মোটর তড়িৎশক্তিকে ঘূর্ণন গতিশক্তিতে রূপান্তরিত করে। বার্লোর চক্রে তড়িৎশক্তি, ঘূর্ণন গতিশক্তিতে রূপান্তরিত হয়, তাই বার্লোর চক্র হল বৈদ্যুতিক মোটর।
বার্লোর চক্রের ঘূর্ণন বেগ কীভাবে বৃদ্ধি করা যায়?
চুম্বকের মেরুশক্তি বাড়ানো হলে বা তড়িৎপ্রবাহ বৃদ্ধি করা হলে বার্লোর চক্রের ঘূর্ণন বেগ বৃদ্ধি পায় অর্থাৎ আরও জোরে ঘোরে।
একটি বৃত্তাকার পরিবাহী কুণ্ডলীতে তড়িৎপ্রবাহ পাঠালে কোনদিকে কোন্ চৌম্বক মেরুর সৃষ্টি হয়?
কুণ্ডলীর যে প্রান্তের দিকে অক্ষ বরাবর তাকালে কুণ্ডলীর মধ্য দিয়ে তড়িৎপ্রবাহ ঘড়ির কাঁটার অভিমুখে বা দক্ষিণাবর্তী হয় সেই প্রান্তে দক্ষিণ মেরু ও যে প্রান্তের দিকে অক্ষ বরাবর তাকালে কুণ্ডলীর মধ্য দিয়ে তড়িৎপ্রবাহ ঘড়ির কাঁটার বিপরীত অভিমুখে বা বামাবর্তী হয় সেই প্রান্তে উত্তর মেরুর সৃষ্টি হয়।
বৈদ্যুতিক মোটর কাকে বলে?
বৈদ্যুতিক মোটর হল এমন একটি তড়িৎযন্ত্র যেখানে স্থির চৌম্বক ক্ষেত্রে একটি তড়িদবাহী কুণ্ডলী একটি নির্দিষ্ট অক্ষ সাপেক্ষে আবর্তন করে এবং তড়িৎশক্তি যান্ত্রিক শক্তিতে রূপান্তরিত হয়।
একটি বৈদ্যুতিক মোটরের গঠন ও কার্যপ্রণালী বর্ণনা করো।
গঠন – একটি বৈদ্যুতিক মোটরের মূল অংশগুলি হল –
- ক্ষেত্রচুম্বক
- আর্মেচার
- কম্যুটেটর
- ব্রাশ
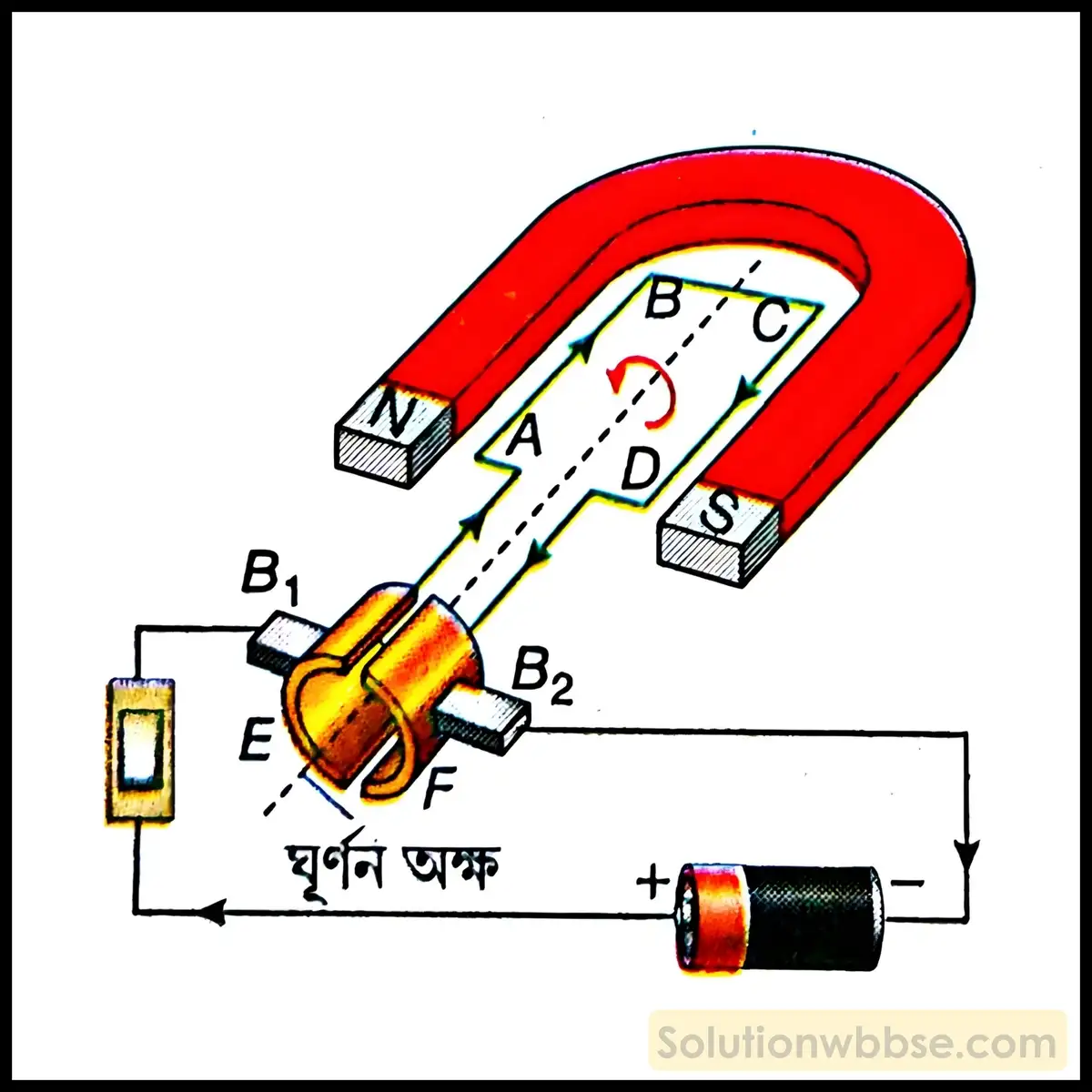
- ক্ষেত্রচুম্বক – বৈদ্যুতিক মোটরে একটি শক্তিশালী অশ্বক্ষুরাকৃতি চুম্বক থাকে। একে ক্ষেত্রচুম্বক (field magnet) বলা হয়। তবে এটি সাধারণত তড়িৎচুম্বক হয়। নরম লোহার ওপর অন্তরিত তামার তার জড়িয়ে তড়িৎপ্রবাহ পাঠিয়ে ক্ষেত্রচুম্বক তৈরি করা হয়। একক দৈর্ঘ্যে পাকসংখ্যা বাড়িয়ে বা তড়িৎপ্রবাহ বাড়িয়ে চুম্বকের শক্তি বৃদ্ধি করা যায়।
- আর্মেচার – ক্ষেত্রচুম্বকের মেরু দুটির মাঝে একটি অন্তরিত তামার তারের আয়তাকার কুণ্ডলী ABCD রাখা হয়। কুণ্ডলীটি নরম লোহার চোঙের ওপর গঠন করা হয়, একে আর্মেচার বলা হয়। কুণ্ডলীটি এমনভাবে রাখা থাকে যাতে কুণ্ডলীর AB ও CD বাহু চৌম্বক ক্ষেত্রের সঙ্গে সমকোণে থাকে।
- কম্যুটেটর – আর্মেচারের দুটি প্রান্ত পিতলের তৈরি দুটি অর্ধবলয় E ও F -এর সঙ্গে যুক্ত। একে কম্যুটেটর বলা হয়। অর্ধবলয় দুটির ভিতরটি অন্তরিত এবং একটি অক্ষদণ্ড (axle) -এর সঙ্গে যুক্ত। আর্মেচার ঘুরলে অর্ধবলয় দুটিও একই সঙ্গে ঘোরে।
- ব্রাশ – অর্ধবলয় দুটির বাইরের অংশ দুটি পরিবাহী কার্বন ব্রাশ B1 ও B2 -এর সঙ্গে স্পর্শ করে থাকে। ব্রাশ দুটির সঙ্গে পরিবাহী তার দিয়ে একটি ব্যাটারি ও সুইচ যুক্ত করা হয়।
কার্যপ্রণালী – সুইচ অন করলে আর্মেচারটি চিত্রানুযায়ী বা ঘড়ির কাঁটার বিপরীত অভিমুখে ঘোরে। এর কারণ হল চিত্রানুযায়ী তড়িৎপ্রবাহ পাঠানো হলে কুণ্ডলীতে AB বাহুতে A থেকে B -এর দিকে এবং CD বাহুতে C থেকে D -এর দিকে তড়িৎপ্রবাহ হয়। তাই ফ্লেমিং -এর বাম হস্ত নিয়ম অনুযায়ী, AB বাহুর ওপর, নীচের দিকে ও CD বাহুর ওপর, ওপরের দিকে বল ক্রিয়া করে। ফলে AB বাহু নীচের দিকে ও CD বাহু ওপরের দিকে গতিশীল হয়। যখন ABCD কুণ্ডলীটি খাড়া হয় তখন E ও F অর্ধবলয় দুটির ফাঁকে B1 ও B2 ব্রাশ দুটি আসে এবং তড়িৎসংযোগ বিচ্ছিন্ন হয়। তবে গতিজাড্যের জন্য F অর্ধবলয় B1 ব্রাশকে ও E অর্ধবলয় B2 ব্রাশকে স্পর্শ করে। ফলে AB বাহুতে প্রবাহমাত্রা B থেকে A -এর দিকে এবং CD বাহুতে প্রবাহমাত্রা D থেকে C -এর দিকে হয়। এই অবস্থায় ফ্লেমিং -এর বাম হস্ত নিয়ম অনুযায়ী AB বাহু ওপরের দিকে ও CD বাহু নীচের দিকে গতিশীল হয়। এইভাবে বর্তনীতে তড়িৎপ্রবাহ চলতে থাকলে আর্মেচার একই অভিমুখে ঘুরতে থাকে।
একটি dc মোটর ঘড়ির কাঁটার অভিমুখে ঘুরছে। এই অভিমুখ কীভাবে পরিবর্তন করা যাবে?
চুম্বকের মেরুরদিকে উল্টে দিলে বা তড়িৎপ্রবাহের অভিমুখ বিপরীত করা হলে dc ভেক্টরের ঘূর্ণন অভিমুখ বিপরীত হবে অর্থাৎ ঘড়ির কাঁটার বিপরীত অভিমুখ ঘুরবে।
বৈদ্যুতিক মোটরের ব্যবহার লেখো। বৈদ্যুতিক মোটরে আর্মেচারের ঘূর্ণন বেগ কীভাবে বাড়ানো যায়?
বৈদ্যুতিক পাখা, MP3 মেসিন, পাম্প, ট্রেন, রোলিং মিল প্রভৃতিতে বৈদ্যুতিক মোটর ব্যবহৃত হয়।
আর্মেচার কুণ্ডলীর পাকসংখ্যা বাড়িয়ে বা প্রবাহমাত্রা বাড়িয়ে বা ক্ষেত্রচুম্বকের শক্তি বাড়িয়ে আর্মেচারের ঘূর্ণন বেগ বাড়ানো যায়।
একটি চুম্বক শলাকার কোনটি উত্তর মেরু ও কোনটি দক্ষিণ মেরু তা লেখা নেই। একটি পরিবাহী তার ও একটি ব্যাটারির সাহায্যে কীভাবে চুম্বকের মেরু শনাক্ত করবে?
পরিবাহী তারটিকে ব্যাটারির সঙ্গে যুক্ত করা হল। এবার তারটিকে এমনভাবে রাখা হল যাতে তারে তড়িৎপ্রবাহ দক্ষিণ থেকে উত্তরে হয়। এবার চুম্বক শলাকাটিকে তারের নীচে রাখলে যে মেরুটি পশ্চিমদিকে বিক্ষিপ্ত হবে সেটি হল উত্তর মেরু, অন্যটি হল দক্ষিণ মেরু।
একটি ব্যাটারির কোনটি ধনাত্মক মেরু ও কোনটি ঋণাত্মক মেরু তা লেখা নেই। একটি পরিবাহী তার ও একটি চুম্বক শলাকার সাহায্যে কীভাবে ব্যাটারির মেরু শনাক্ত করবে?
স্বাভাবিক অবস্থায় চুম্বক শলাকা উত্তর-দক্ষিণ দিক বরাবর মুখ করে থাকে। পরিবাহী তারটিকে ব্যাটারির সঙ্গে যুক্ত করে উত্তর-দক্ষিণ দিক বরাবর রাখা হল। এবার চুম্বক শলাকাটিকে তারের নীচে রাখলে যদি উত্তর মেরুর পশ্চিম দিকে বিক্ষেপ হয় তাহলে দক্ষিণ প্রান্তের তারটি ব্যাটারির যে মেরুর সঙ্গে যুক্ত সেটি ধনাত্মক মেরু এবং যদি উত্তর মেরুর পূর্ব দিকে বিক্ষেপ হয় তাহলে উত্তর প্রান্তের তারটি ব্যাটারির যে মেরুর সঙ্গে যুক্ত সেটি ধনাত্মক মেরু।
তড়িৎ চুম্বকীয় আবেশ, বৈদ্যুতিক জেনারেটর, ও গৃহস্থালির বৈদ্যুতিক বর্তনী
চৌম্বক প্রবাহ কাকে বলে?
চৌম্বক ক্ষেত্রে অবস্থিত কোনো তলের মধ্য দিয়ে লম্বভাবে অতিক্রান্ত চৌম্বক বলরেখার সংখ্যাকে চৌম্বক প্রবাহ বলা হয়।
তড়িৎচুম্বকীয় আবেশ ও আবিষ্ট তড়িৎপ্রবাহ কাকে বলে?
তড়িৎচুম্বকীয় আবেশ – কোনো বদ্ধ কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হলে কুণ্ডলীতে একটি তড়িৎচালক বল আবিষ্ট হয়। এই ঘটনাকে তড়িৎচুম্বকীয় আবেশ বলা হয়।
আবিষ্ট তড়িৎপ্রবাহ – কোনো বদ্ধ কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হলে কুণ্ডলীতে যে তড়িৎপ্রবাহ চলে তাকে আবিষ্ট তড়িৎপ্রবাহ বলা হয়।
আবিষ্ট তড়িৎচালক বল কাকে বলে?
কোনো বদ্ধ কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হলে কুণ্ডলীতে যে তড়িৎচালক বলের উদ্ভব হয়, তাকে আবিষ্ট তড়িৎচালক বল বলা হয়।
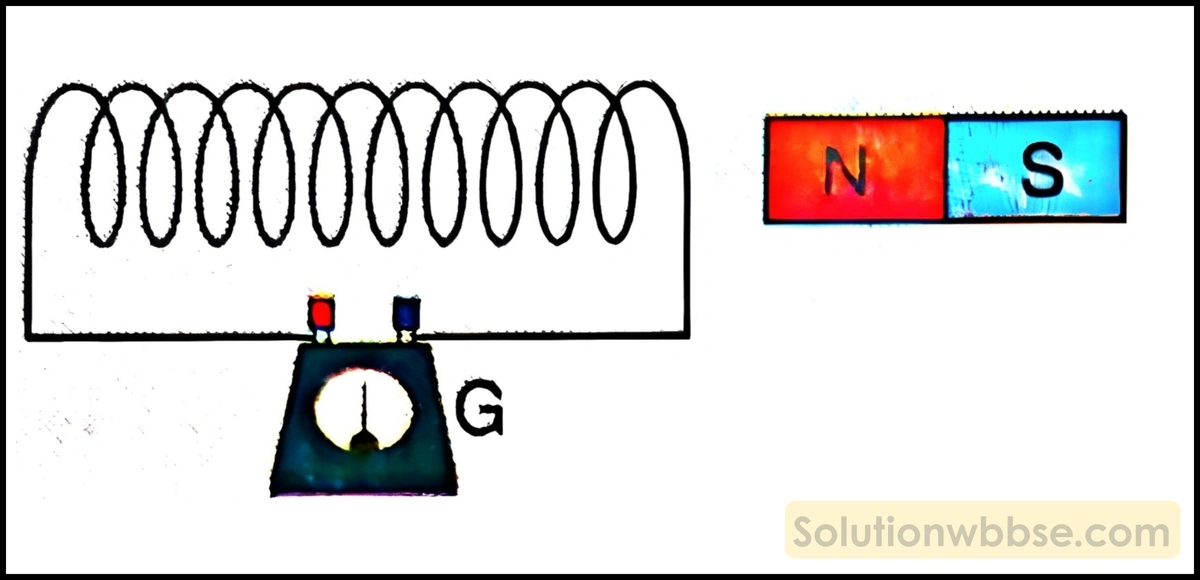
একটি তারের কুণ্ডলী, একটি দণ্ডচুম্বক ও একটি গ্যালভানোমিটারের সাহায্যে তড়িৎচুম্বকীয় আবেশ পরীক্ষার সাহায্যে ব্যাখ্যা করো।
পরীক্ষা – একটি তারের কুণ্ডলীকে একটি গ্যালভানোমিটারের সঙ্গে চিত্রের মতো যুক্ত করা হল। এই অবস্থায় গ্যালভানোমিটারের কাঁটাটি ‘0’ দাগে থাকে। এবার একটি দণ্ডচুম্বকের N মেরুকে দ্রুত কুণ্ডলীর অক্ষ বরাবর কুণ্ডলীর দিকে নিয়ে গেলে দেখা যাবে গ্যালভানোমিটারের কাঁটা বিক্ষিপ্ত হচ্ছে। দণ্ডচুম্বককে কুণ্ডলীর সামনে স্থির রাখলে গ্যালভানোমিটারের কাঁটার কোনো বিক্ষেপ হয় না। এবার দণ্ডচুম্বকের N মেরুকে কুণ্ডলীর সামনে থেকে দ্রুত সরিয়ে আনা হল। দেখা গেল গ্যালভানোমিটারের কাঁটার বিক্ষেপ হচ্ছে, তবে পূর্বের বিক্ষেপের বিপরীত দিকে।
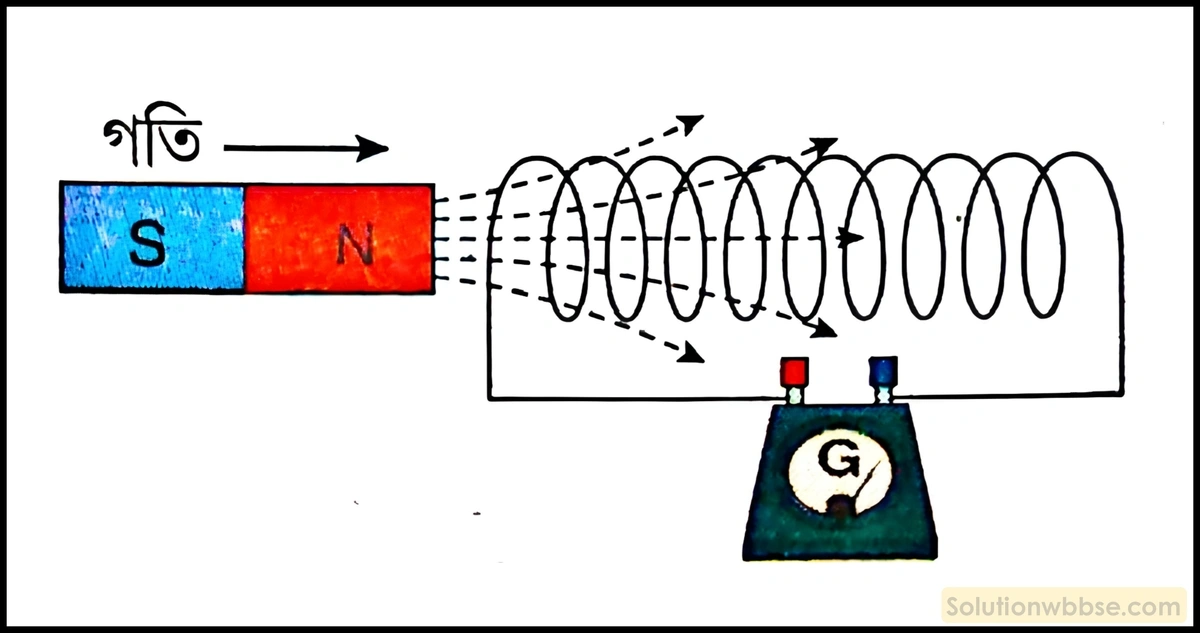
সিদ্ধান্ত – দণ্ডচুম্বকটিকে যখন কুণ্ডলীর সামনে স্থির রাখা হয় তখন কুণ্ডলীতে তড়িৎপ্রবাহ হয় না, শুধুমাত্র চুম্বকটি কুণ্ডলীর দিকে এলে বা দূরে সরে গেলে কুণ্ডলীতে তড়িৎপ্রবাহ হয়। এর কারণ হল, চুম্বকটি যখন স্থির ছিল তখন কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহ স্থির ছিল। কিন্তু চুম্বকটি যখন কুণ্ডলীর দিকে গতিশীল হয় তখন কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহ বৃদ্ধি পায়। আবার চুম্বকটিকে যখন কুণ্ডলী থেকে দূরে সরানো হয় তখন কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহ হ্রাস পায় অর্থাৎ এই দুই ক্ষেত্রে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হয়। সুতরাং বলা যায়, কোনো বদ্ধ কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহ পরিবর্তিত হলে কুণ্ডলীতে তড়িৎচালক বল আবিষ্ট হয় এবং কুণ্ডলীতে তড়িৎপ্রবাহ হয়। এই দুই ক্ষেত্রে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হলেও এই দুই পরিবর্তন বিপরীত, প্রথম ক্ষেত্রে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহ বৃদ্ধি পায় ও দ্বিতীয় ক্ষেত্রে হ্রাস পায়। তাই দুই ক্ষেত্রে তড়িৎপ্রবাহ বিপরীত দিকে হয় বলে গ্যালভানোমিটার কাঁটার বিক্ষেপ দুই ক্ষেত্রে বিপরীত দিকে হয়।
একটি তড়িৎকোশ, তারের কুণ্ডলী ও একটি গ্যালভানোমিটারের সাহায্যে তড়িৎচুম্বকীয় আবেশ পরীক্ষার সাহায্যে ব্যাখ্যা করো।
পরীক্ষা – একটি কুণ্ডলীকে একটি গ্যালভানোমিটারের সঙ্গে যুক্ত করে স্থিরভাবে রাখা হল। অন্য একটি কুণ্ডলীর সঙ্গে
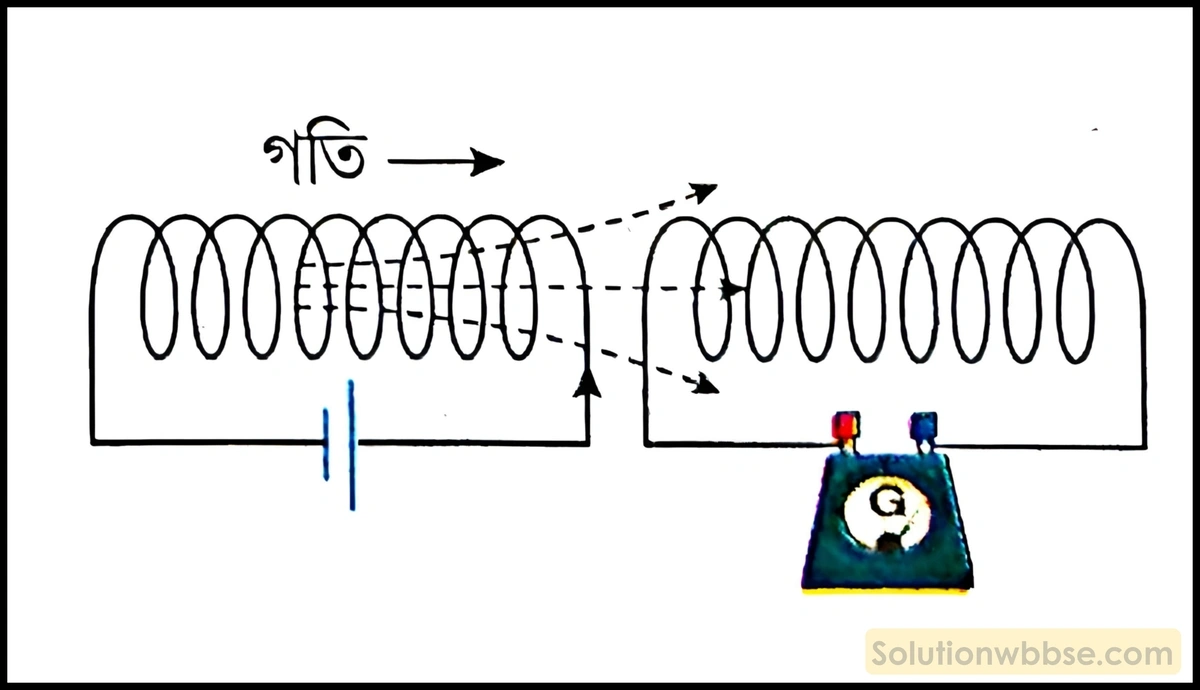
একটি তড়িৎকোশ যুক্ত করে প্রথম কুণ্ডলীর সঙ্গে সমাক্ষভাবে একটু দূরে রাখা হল। এই অবস্থায় গ্যালভানোমিটারের কাঁটাটি ‘0’ দাগে থাকে। এবার দ্বিতীয় কুণ্ডলীকে প্রথম কুণ্ডলীর অক্ষ বরাবর দ্রুত কাছে নিয়ে গেলে দেখা যাবে গ্যালভানোমিটারের কাঁটা বিক্ষিপ্ত হচ্ছে। দ্বিতীয় কুণ্ডলীকে প্রথম কুণ্ডলীর সামনে স্থির রাখলে গ্যালভানোমিটার কাঁটার কোনো বিক্ষেপ হয় না। এবার দ্বিতীয় কুণ্ডলীকে প্রথম কুণ্ডলীর সামনে থেকে অক্ষ বরাবর দ্রুত সরিয়ে নিয়ে গেলে দেখা যাবে গ্যালভানোমিটারের কাঁটার বিক্ষেপ হচ্ছে, তবে পূর্বের সাপেক্ষে বিপরীত দিকে।
সিদ্ধান্ত – দ্বিতীয় কুণ্ডলীর মধ্য দিয়ে তড়িৎপ্রবাহ পাঠালে এটি দণ্ডচুম্বকের মতো আচরণ করে এবং বলরেখা নির্গত হয়। দ্বিতীয় কুণ্ডলীকে যখন প্রথম কুণ্ডলীর সামনে স্থির রাখা হয় তখন প্রথম কুণ্ডলীতে কোনো তড়িৎপ্রবাহ হয় না, কিন্তু দ্বিতীয় কুণ্ডলীকে প্রথম কুণ্ডলীর কাছে নিয়ে এলে বা দূরে সরিয়ে নিয়ে গেলে প্রথম কুণ্ডলীতে তড়িৎপ্রবাহ হয়। এর কারণ হল, দ্বিতীয় কুণ্ডলীটি যখন প্রথম কুণ্ডলীর সামনে স্থির ছিল তখন প্রথম কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহ স্থির ছিল কিন্তু দ্বিতীয় কুণ্ডলীকে প্রথম কুণ্ডলীর কাছে নিয়ে এলে বা সরিয়ে নিয়ে গেলে প্রথম কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহ যথাক্রমে বৃদ্ধি ও হ্রাস পায়। অর্থাৎ প্রথম কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হয় তাই ওই কুণ্ডলীতে তড়িৎচালক বল আবিষ্ট হয় এবং বর্তনীতে তড়িৎপ্রবাহ চলে। তবে এই দুই ক্ষেত্রে প্রথম কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন বিপরীত, তাই দুই ক্ষেত্রে তড়িৎপ্রবাহের অভিমুখ বিপরীত হয় বলে গ্যালভানোমিটার কাঁটার বিক্ষেপও বিপরীত দিকে হয়।
গ্যালভানোমিটার কী?
গ্যালভানোমিটার হল এমন একটি তড়িৎযন্ত্র যা বর্তনীতে তড়িৎপ্রবাহের অস্তিত্ব নির্দেশ করে। এর কাঁটাটি ‘0 ‘দাগে থাকে যখন বর্তনীতে কোনো তড়িৎপ্রবাহ হয় না। কাঁটাটি তড়িৎপ্রবাহের অভিমুখ অনুযায়ী ‘0’ দাগের উভয়দিকে বিক্ষিপ্ত হয়।

তড়িৎচুম্বকীয় আবেশ-সংক্রান্ত ফ্যারাডের সূত্র দুটি লেখো।
তড়িৎচুম্বকীয় আবেশ-সংক্রান্ত ফ্যারাডের সূত্রাবলি –
- প্রথম সূত্র – কোনো বদ্ধ কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হলে কুণ্ডলীতে তড়িৎচালক বল আবিষ্ট হয় এবং কুণ্ডলীতে তড়িৎপ্রবাহ চলে।
- দ্বিতীয় সূত্র – তড়িৎচুম্বকীয় আবেশের ক্ষেত্রে আবিষ্ট তড়িৎচালক বলের মান কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তনের হারের সঙ্গে সমানুপাতিক।
চৌম্বক প্রবাহের CGS ও SI পদ্ধতিতে একক লেখো।
চৌম্বক প্রবাহের CGS পদ্ধতি ও SI -তে একক যথাক্রমে maxwell ও Wb (weber)।
1 Wb = 108 maxwell
লেঞ্জের সূত্রটি লেখো ও শক্তির সংরক্ষণ নীতির সাহায্যে ব্যাখ্যা করো।
লেঞ্জের সূত্র – তড়িৎচুম্বকীয় আবেশের ক্ষেত্রে আবিষ্ট তড়িৎপ্রবাহ এমন একটি অভিমুখে হবে যাতে, যে কারণে প্রবাহের সৃষ্টি হয় প্রবাহ সর্বদা সেই কারণকে বাধা দেয়।
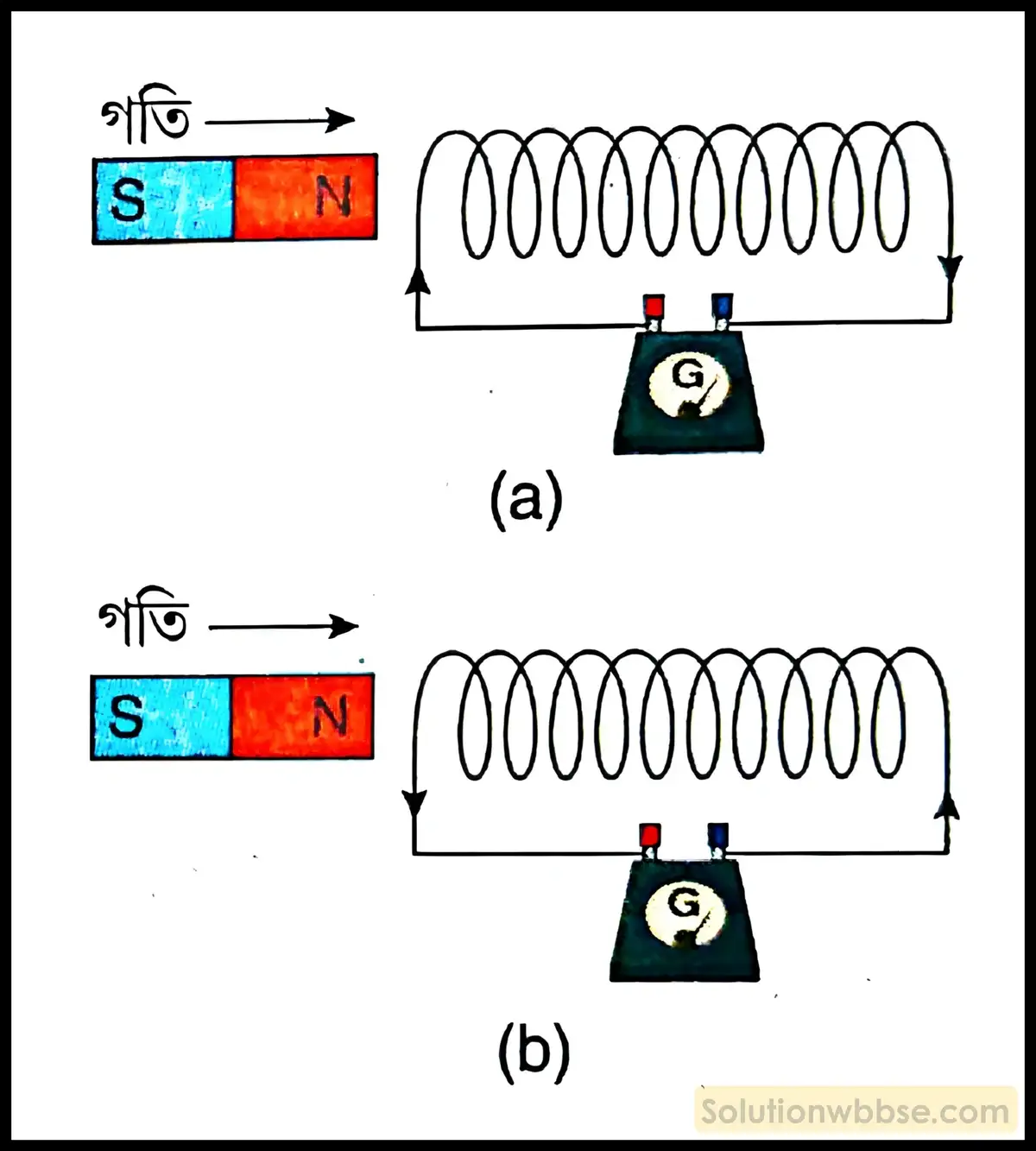
শক্তির সংরক্ষণ নীতির সাহায্যে ব্যাখ্যা – মনে করি, দণ্ডচুম্বকের N মেরুকে কোনো বদ্ধ কুণ্ডলীর দিকে অক্ষ বরাবর আনার জন্য কুণ্ডলীতে আবিষ্ট তড়িৎপ্রবাহের অভিমুখ হয় দক্ষিণাবর্তী (clockwise) অর্থাৎ কুণ্ডলীর সম্মুখ প্রান্তে S মেরু উৎপন্ন হয়। এই সৃষ্ট S মেরু দণ্ডচুম্বকের N মেরুকে আকর্ষণ করে। ফলে দণ্ডচুম্বকটি কুণ্ডলীর দিকে ত্বরণসহ অগ্রসর হয়। এক্ষেত্রে দেখা যাচ্ছে বাহ্যিক কোনো শক্তির সরবরাহ ছাড়াই চুম্বকের গতিশক্তি ও তড়িৎশক্তি পাওয়া যাচ্ছে যা শক্তির সংরক্ষণ নীতি অনুযায়ী অসম্ভব। সুতরাং, দণ্ডচুম্বকের N মেরু যখন কুণ্ডলীর দিকে অক্ষ বরাবর অগ্রসর হবে তখন কুণ্ডলীতে তড়িৎপ্রবাহ হবে বামাবর্তী (anticlockwise)। ফলে কুণ্ডলীর সম্মুখ প্রান্তে N মেরুর সৃষ্টি হবে যা দণ্ডচুম্বকের N মেরুকে বিকর্ষণ করবে। এই বিকর্ষণ বলের বিরুদ্ধে দণ্ডচুম্বককে কুণ্ডলীর দিকে অক্ষ বরাবর নিয়ে যেতে গেলে যান্ত্রিক কার্য করতে হবে। এই যান্ত্রিক কার্যই তড়িৎশক্তিতে রূপান্তরিত হয়। অর্থাৎ আবিষ্ট তড়িৎপ্রবাহ এমন অভিমুখে হবে যাতে, যে কারণে প্রবাহের সৃষ্টি হয় প্রবাহ সর্বদা সেই কারণকে বাধা দেয় – এটিই হল লেঞ্জের সূত্র।
একটি বৃত্তাকার পরিবাহীর অক্ষ বরাবর কোনো দণ্ডচুম্বককে গতিশীল করলে আবিষ্ট তড়িৎপ্রবাহের অভিমুখ অভিমুখের চিত্র অঙ্কন করো।
একটি বৃত্তাকার পরিবাহীর অক্ষ বরাবর কোনো দণ্ডচুম্বককে গতিশীল করলে আবিষ্ট তড়িৎপ্রবাহের অভিমুখ যা হবে তা নীচের চিত্রে দেওয়া হল।
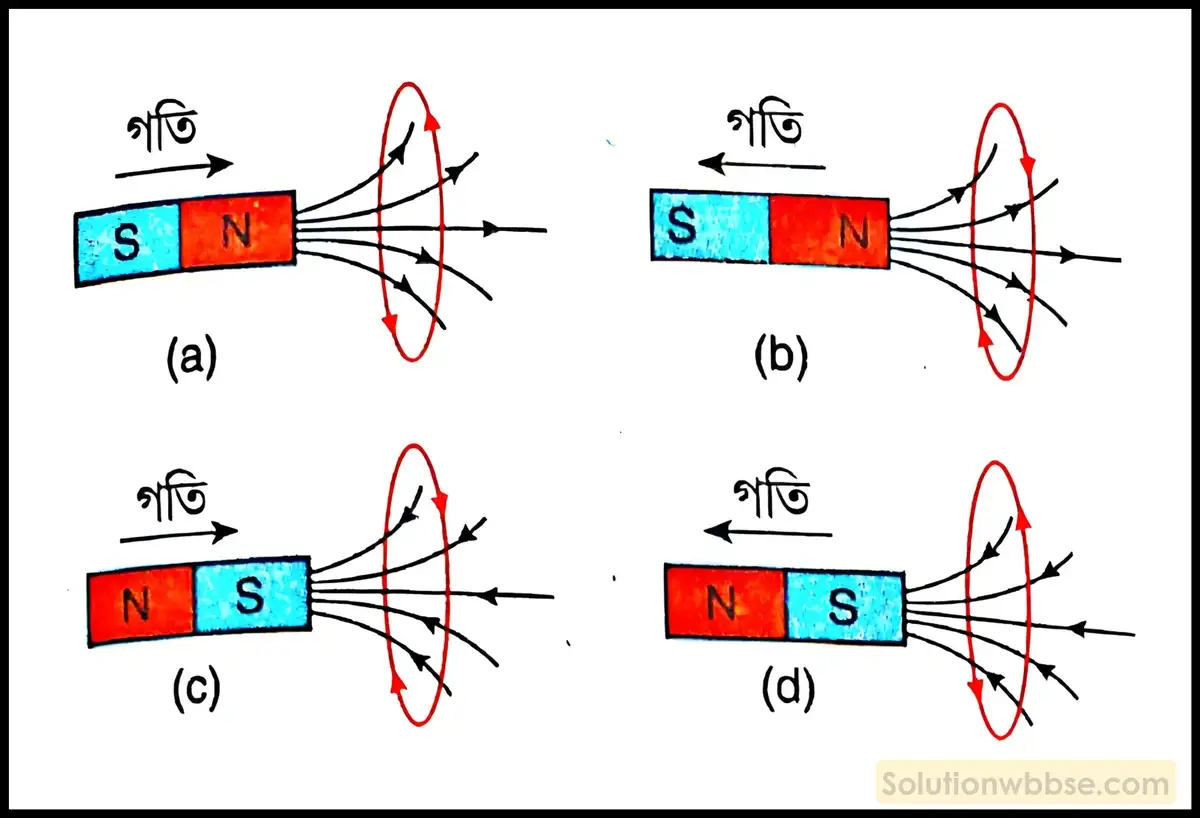
লেঞ্জের সূত্রের সাহায্যে শক্তির সংরক্ষণ নীতি ব্যাখ্যা করো।
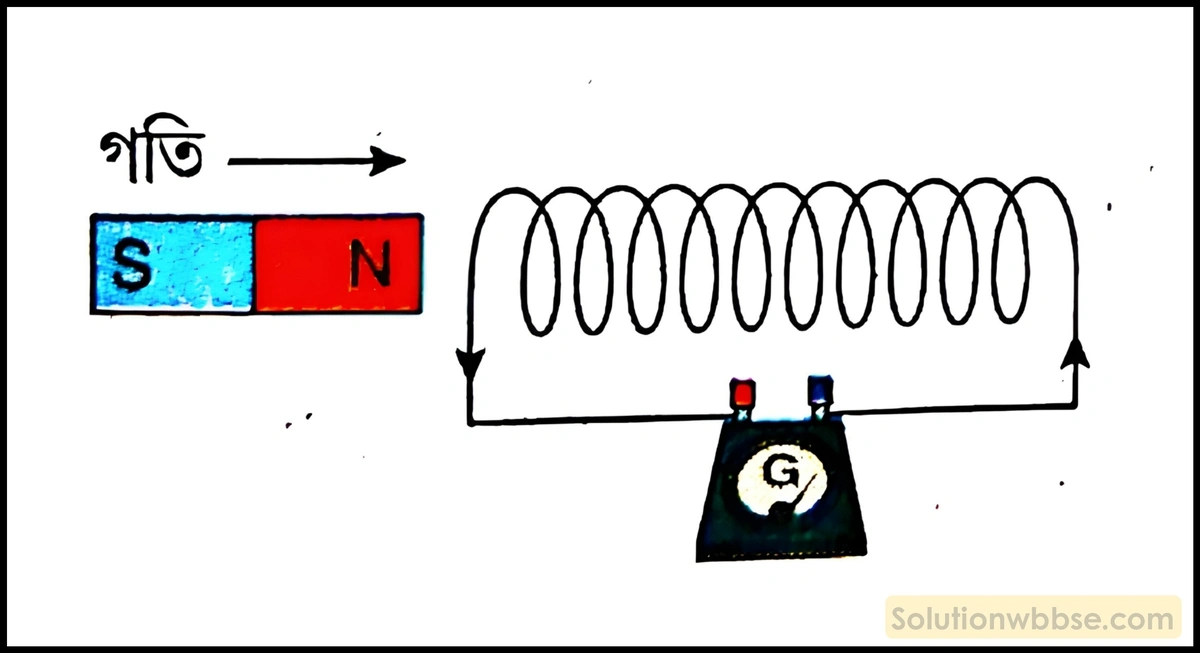
মনে করি, একটি দণ্ডচুম্বকের N মেরুকে, গ্যালভানোমিটারের সঙ্গে যুক্ত একটি বদ্ধ কুণ্ডলীর অক্ষ বরাবর দ্রুত কাছে আনা হল। ফলে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহ বৃদ্ধি পাবে অর্থাৎ কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হবে। ফলে কুণ্ডলীতে তড়িৎচালক বল আবিষ্ট হবে ও তড়িৎপ্রবাহ চলবে। লেঞ্জের সূত্রানুযায়ী, এই তড়িৎপ্রবাহ এমন অভিমুখে হবে যাতে যে কারণে প্রবাহ সৃষ্টি হয় প্রবাহ সর্বদা সেই কারণকে বাধা দেবে অর্থাৎ কুণ্ডলীর সম্মুখপ্রান্তে তড়িৎপ্রবাহ হবে বামাবর্তী এবং সম্মুখপ্রান্তে উত্তর মেরু সৃষ্টি হবে। এই সৃষ্ট উত্তর মেরু দণ্ডচুম্বকের উত্তর মেরুকে বিকর্ষণ করবে। এই বিকর্ষণ বলের বিরুদ্ধে দণ্ডচুম্বককে কুণ্ডলীর দিকে আনার জন্য যান্ত্রিক কার্য করতে হবে। বাহ্যিক সংস্থা দ্বারা এই যান্ত্রিক কার্যই তড়িৎশক্তিতে রূপান্তরিত হয়। এটিই হল শক্তির সংরক্ষণ নীতি।
একটি তামার রিং -কে অনুভূমিকভাবে রেখে একটি দণ্ডচুম্বককে, খাড়া ওপর থেকে নীচে ওই রিং -এর কেন্দ্রের মধ্য দিয়ে অবাধে ফেলা হল। পড়ন্ত চুম্বকটির ত্বরণ অভিকর্ষজ ত্বরণের সমান, বেশি অথবা কী হবে?
দণ্ডচুম্বকটি যখন খাড়াভাবে তামার রিং -এর কেন্দ্রের দিকে পড়ে তখন তামার রিং -এর সঙ্গে জড়িত চৌম্বক প্রবাহ বৃদ্ধি পায়, অর্থাৎ তামার রিং -এর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হয়। ফলে রিং -এ একটি তড়িৎচালক বল আবিষ্ট হয় এবং তড়িৎপ্রবাহ শুরু হয়। আবিষ্ট তড়িৎপ্রবাহ এমন অভিমুখে হবে যাতে তার সৃষ্টির কারণ অর্থাৎ দণ্ডচুম্বকের পতন বাধাপ্রাপ্ত হবে। সুতরাং পতনশীল অবস্থায় দণ্ডচুম্বকের ওপর একটি ঊর্ধ্বমুখী বিকর্ষণ বল ক্রিয়া করবে ফলে দণ্ডচুম্বক অভিকর্ষজ ত্বরণ অপেক্ষা কম ত্বরণে নীচের দিকে পড়বে।
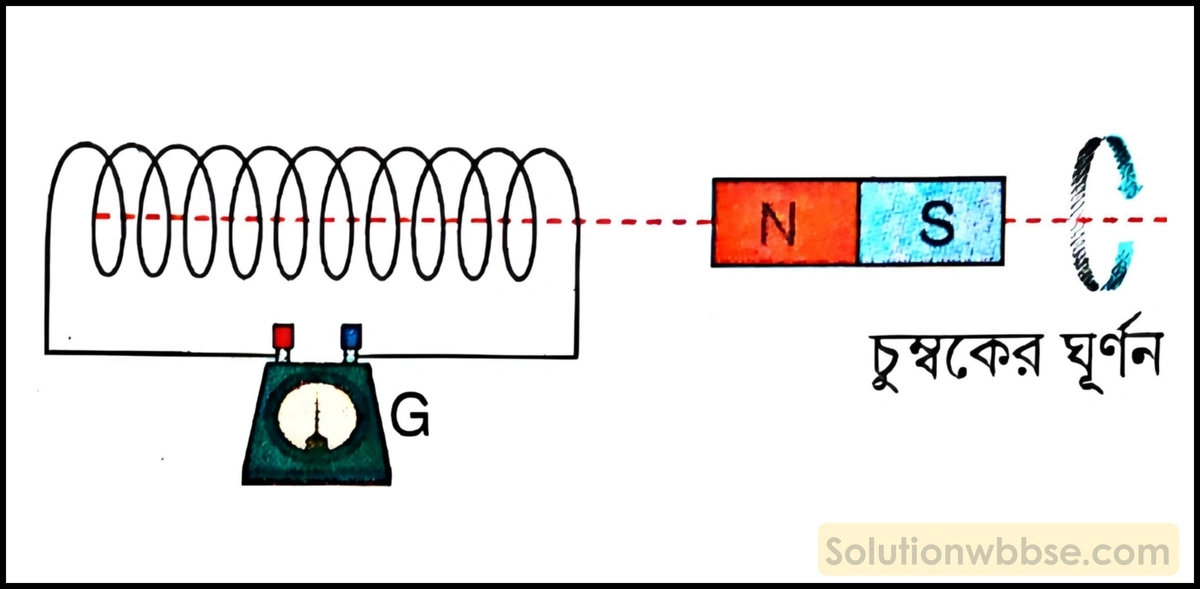
একটি বৃত্তাকার তার কুণ্ডলীর অক্ষ বরাবর একটি চোঙাকৃতি দণ্ডচুম্বক রাখা আছে। চুম্বকটি ওই অক্ষ সাপেক্ষে ঘুরতে থাকলে ওই কুণ্ডলীতে কোনো তড়িৎপ্রবাহ আবিষ্ট হবে কী?
চুম্বকটি বৃত্তাকার কুণ্ডলী ও চুম্বকের সাধারণ অক্ষ সাপেক্ষে ঘুরতে থাকলে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের কোনো পরিবর্তন হয় না, তাই কুণ্ডলীতে কোনো তড়িৎচালক বল আবিষ্ট হয় না। ফলে ওই কুণ্ডলীতে কোনো তড়িৎপ্রবাহ আবিষ্ট হবে না।
একটি পরিবাহী তার বৃত্তের আকারে বাঁকানো হল। বৃত্তাকার তার ও এর কাছে রাখা একটি দীর্ঘ ঋজু পরিবাহী তার AB উভয়েই কাগজের তলে অবস্থিত। যদি A থেকে B অভিমুখে ক্রমবর্ধমান তড়িৎ প্রবাহিত হয়, তবে বৃত্তাকার পরিবাহীতে কোনো তড়িৎপ্রবাহ হবে কী? তড়িৎপ্রবাহ হলে তার অভিমুখ কী হবে?
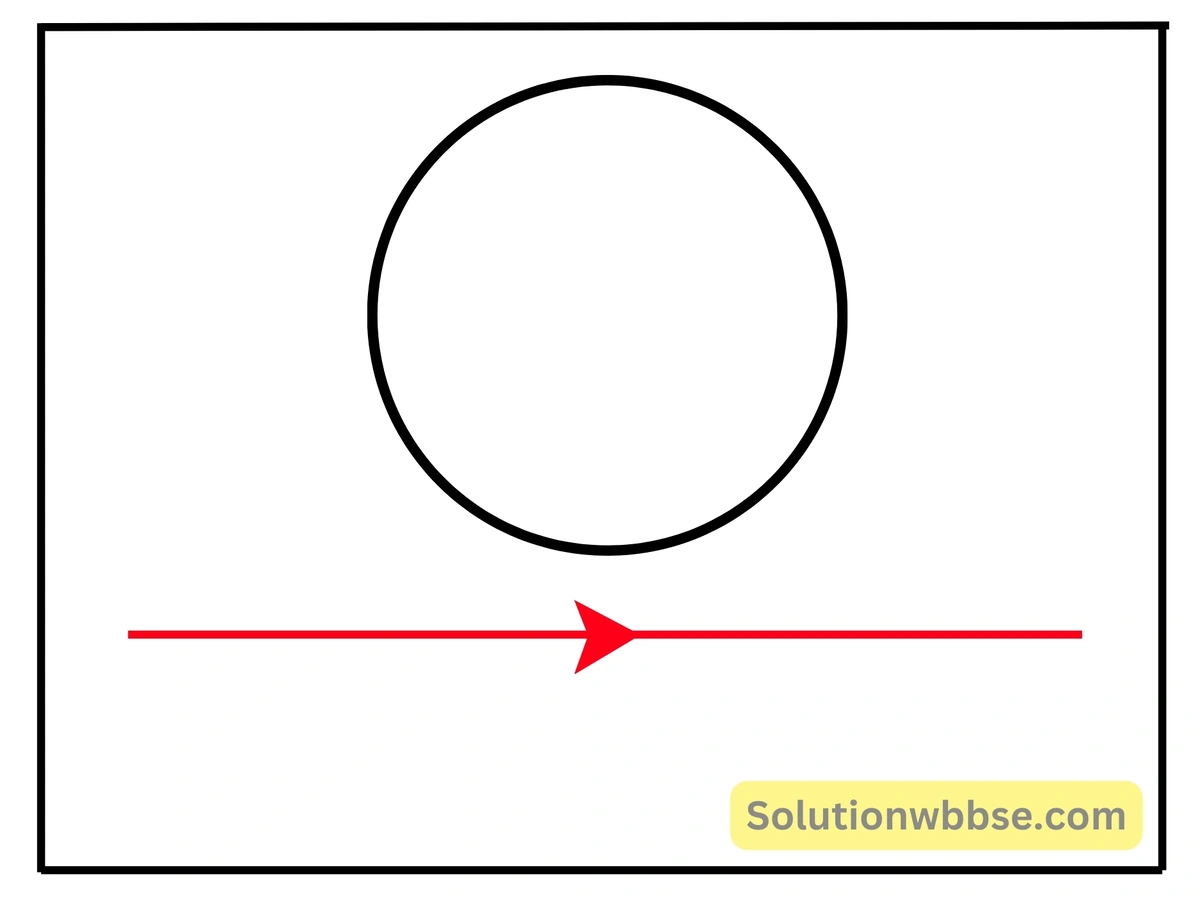
AB তারে তড়িৎপ্রবাহ হলে বৃত্তাকার পরিবাহীর তলের সঙ্গে চৌম্বক প্রবাহ জড়িত হবে। AB তারে তড়িৎপ্রবাহের জন্য চৌম্বক বলরেখাগুলি কেমন হবে তা চিত্রে দেখানো হয়েছে। এখন AB তারে তড়িৎপ্রবাহ পরিবর্তিত হলে বৃত্তাকার পরিবাহীর তলের সঙ্গে জড়িত চৌম্বক প্রবাহ বৃদ্ধি পাবে। ফলে তড়িৎচালক বল আবিষ্ট হবে ও তড়িৎপ্রবাহ চলবে। যেহেতু লেঞ্জের সূত্রানুযায়ী, আবিষ্ট তড়িৎপ্রবাহ এমন অভিমুখে হবে যাতে নিজের সৃষ্টির কারণকেই বাধা দেবে সেহেতু বৃত্তাকার তারে তড়িৎপ্রবাহ ঘড়ির কাঁটার অভিমুখে হবে।
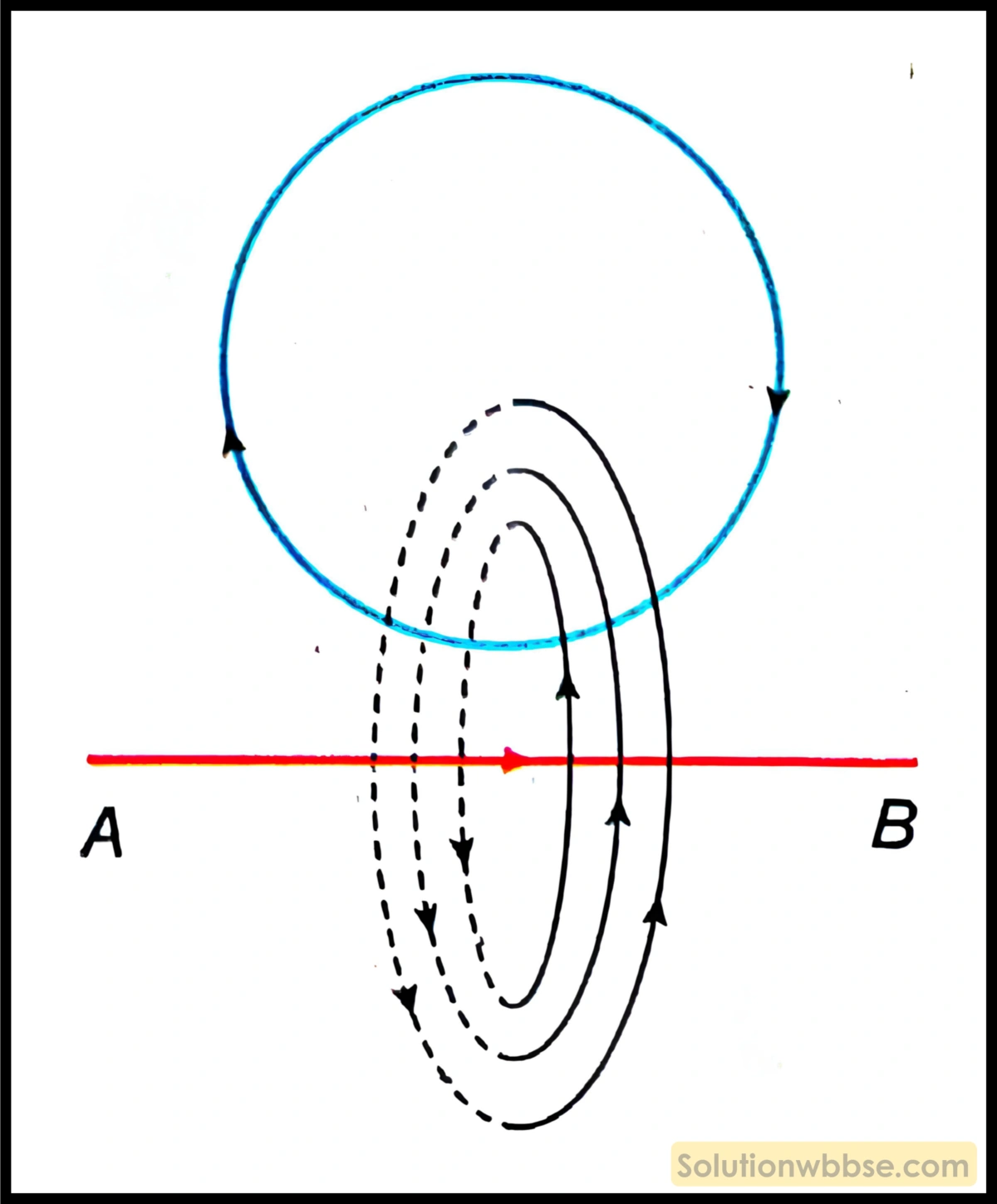
একটি পরিবাহী কুণ্ডলীকে একটি গ্যালভানোমিটারের সঙ্গে যুক্ত করা হল। একটি দণ্ডচুম্বকের N -মেরুকে কুণ্ডলীর ডান প্রান্ত দিয়ে প্রবেশ করিয়ে বাম প্রান্ত দিয়ে বার করা হলে কী হবে?
দণ্ডচুম্বকের N মেরুকে কুণ্ডলীর দিকে আনা হলে কুণ্ডলীর তলের সঙ্গে জড়িত চৌম্বক প্রবাহ বাড়বে। ফলে কুণ্ডলীতে তড়িৎচালক বল আবিষ্ট হবে ও কুণ্ডলীতে তড়িৎপ্রবাহ চলবে। লেঞ্জের সূত্রানুযায়ী, কুণ্ডলীর ডানপ্রান্ত থেকে দেখলে তড়িৎপ্রবাহ হবে ঘড়ির কাঁটার বিপরীত অভিমুখে। আবার চুম্বকটিকে ডানপ্রান্ত দিয়ে বার করার সময় কুণ্ডলীর তলের সঙ্গে জড়িত চৌম্বক প্রবাহ কমতে থাকে। ফলে কুণ্ডলীতে তড়িৎচালক বল আবিষ্ট হবে ও কুণ্ডলীতে তড়িৎপ্রবাহ চলবে। লেঞ্জের সূত্রানুযায়ী, কুণ্ডলীর বামপ্রান্ত থেকে দেখলে তড়িৎপ্রবাহ হবে ঘড়ির কাঁটার বিপরীতে অর্থাৎ ডানপ্রান্ত থেকে দেখলে তড়িৎপ্রবাহ হবে ঘড়ির কাঁটার অভিমুখে। অর্থাৎ দণ্ডচুম্বকের প্রবেশ ও নির্গমনের সময় আবিষ্ট তড়িৎপ্রবাহ বিপরীত অভিমুখে হয়। ফলে গ্যালভানোমিটার কাঁটার বিক্ষেপ দুই ক্ষেত্রে বিপরীত দিকে হবে।
দুটি অভিন্ন দণ্ডচুম্বকের উত্তর মেরুকে দুটি অভিন্ন বদ্ধ বৃত্তাকার পরিবাহী কুণ্ডলীর তলের সমকোণে কেন্দ্র থেকে একই উচ্চতায় রাখা আছে। এবার দুটি দণ্ডচুম্বককেই কুণ্ডলীর কাছে একই উচ্চতায় আনা হল, প্রথমটিকে দ্রুত ও দ্বিতীয়টিকে আস্তে। কোন্ ক্ষেত্রে আবিষ্ট তড়িৎপ্রবাহ বেশি হবে?
প্রথম কুণ্ডলীতে আবিষ্ট তড়িৎপ্রবাহ বেশি হবে কারণ প্রথম দণ্ডচুম্বককে দ্রুততার সঙ্গে আনার জন্য প্রথম কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তনের হার দ্বিতীয়টি অপেক্ষা বেশি হয় ফলে আবিষ্ট তড়িৎচালক বলের মানও বেশি হয়। ফলে আবিষ্ট তড়িৎপ্রবাহ দ্বিতীয়টি অপেক্ষা বেশি হয়।
একটি বৃত্তাকার পরিবাহী কুণ্ডলীর অক্ষ বরাবর একটি দণ্ডচুম্বক রাখা আছে। এবার কুণ্ডলী ও দণ্ডচুম্বক উভয়কেই একইদিকে একই বেগে গতিশীল করা হলে কুণ্ডলীতে কোনো তড়িৎপ্রবাহ আবিষ্ট হবে কী?
কুণ্ডলী ও দণ্ডচুম্বক উভয়কেই একইদিকে একই বেগে গতিশীল করা হলে কুণ্ডলী ও দণ্ডচুম্বকের মধ্যে কোনো আপেক্ষিক বেগ থাকে না, ফলে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের কোনো পরিবর্তন হয় না। তাই কুণ্ডলীতে কোনো তড়িৎচালক বল আবিষ্ট হয় না। ফলে ওই কুণ্ডলীতে কোনো তড়িৎপ্রবাহ আবিষ্ট হবে না।
একমুখী তড়িৎপ্রবাহ বা dc ও পরিবর্তী তড়িৎপ্রবাহ বা ac বলতে কী বোঝ?
একমুখী তড়িৎপ্রবাহ বা dc – তড়িৎপ্রবাহের অভিমুখ সর্বদা একইদিকে হলে তাকে একমুখী তড়িৎপ্রবাহ বা dc বলা হয়।
পরিবর্তী তড়িৎপ্রবাহ বা ac – যে তড়িৎপ্রবাহের অভিমুখ নির্দিষ্ট সময় অন্তর পর্যায়ক্রমে বিপরীত হয় তাকে পরিবর্তী তড়িৎপ্রবাহ বা ac বলা হয়।
(a) ও (b) নং চিত্রে সময়ের (t) পরিবর্তনের সঙ্গে তড়িৎপ্রবাহের (I) পরিবর্তন লেখচিত্রের সাহায্যে দেখানো হয়েছে। (a) চিত্রে প্রবাহমাত্রার অভিমুখ পরিবর্তন হয় না কিন্তু (b) নং চিত্রে প্রবাহমাত্রার অভিমুখ নির্দিষ্ট সময় অন্তর পর্যায়ক্রমে বিপরীত হচ্ছে। তাই (a) চিত্রে তড়িৎপ্রবাহ হল dc এবং (b) চিত্রে তড়িৎপ্রবাহ হল ac।
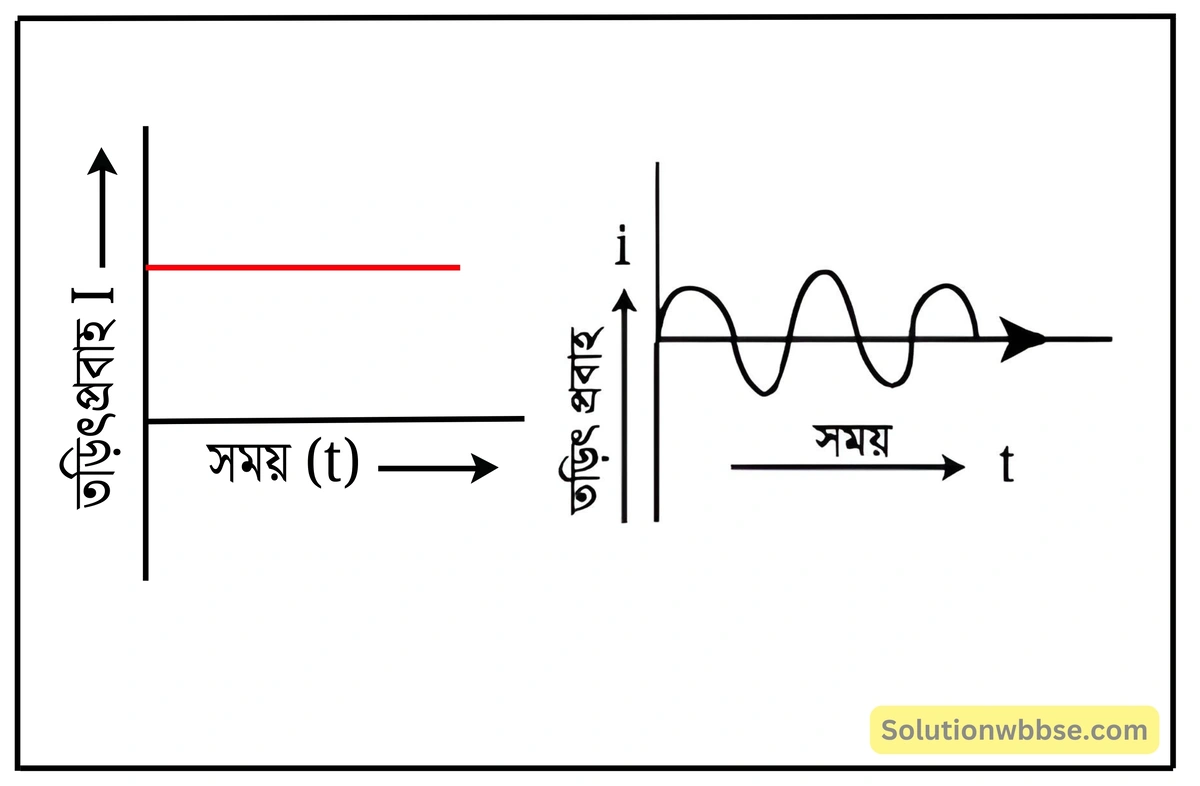
ভারতবর্ষে এবং USA -তে ব্যবহৃত কম্পাঙ্ক কত Hz?
ভারতবর্ষে যে ac ব্যবহার করা হয় তার কম্পাঙ্ক 50 Hz এবং USA -তে যে ac ব্যবহার করা হয় তার কম্পাঙ্ক 60Hz।
dc অপেক্ষা ac -এর সুবিধাগুলি লেখো।
dc অপেক্ষা ac -এর সুবিধাগুলি হল –
- ট্রান্সফরমারের সাহায্যে ac -কে প্রয়োজনমতো নিম্নবিভব থেকে উচ্চবিভবে [step-up ট্রান্সফরমার] ও উচ্চবিভব থেকে নিম্নবিভবে [step-down ট্রান্সফরমার] রূপান্তরিত করা যায়, dc -তে এই সুবিধা পাওয়া যায় না।
- জেনারেটরের সাহায্যে dc অপেক্ষা ac উৎপাদনের খরচ কম।
- তড়িৎ পরিবহণে ac -তে শক্তিক্ষয় তুলনামূলকভাবে কম হয়।
ডায়নামো কাকে বলে? ডায়নামো কয় প্রকার ও কী কী?
ডায়নামো – যে যন্ত্রে তড়িৎচুম্বকীয় আবেশের নীতিকে কাজে লাগিয়ে চৌম্বক ক্ষেত্রে পরিবাহী কুণ্ডলীকে ঘুরিয়ে যান্ত্রিক শক্তিকে তড়িৎশক্তিতে রূপান্তরিত করা যায় তাকে ডায়নামো বলা হয়।
ডায়নামো সাধারণত দু-প্রকার –
- ac ডায়নামো ও
- dc ডায়নামো।
তড়িৎবিশ্লেষণ, তড়িৎলেপন, ব্যাটারি চার্জ ac -তে হয় না dc -তে হয়?
তড়িৎবিশ্লেষণ, তড়িৎলেপন, ব্যাটারি চার্জ ac -তে হয় না, dc -তে হয়।
একটি ac ডায়নামোর কার্যনীতির সংক্ষিপ্ত আলোচনা করো।
নীচের চিত্রে একটি ac ডায়নামোর মূল অংশ দেখানো হয়েছে। এর মূল অংশগুলি হল – ক্ষেত্রচুম্বক, আর্মেচার, স্লিপ রিং
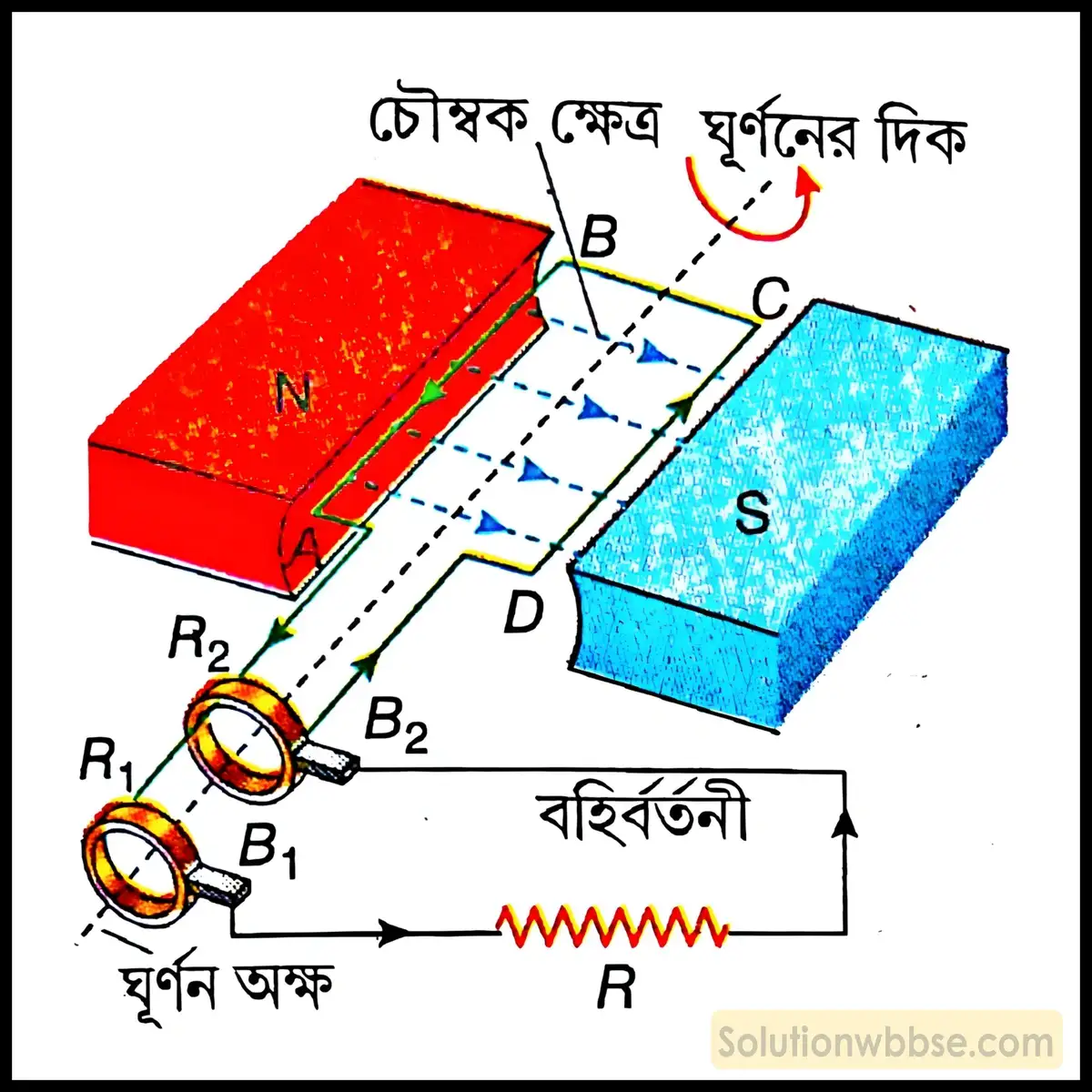
ও ব্রাশ। N ও S হল একটি অশ্বক্ষুরাকৃতি চুম্বকের দুটি মেরু, এটিকে ক্ষেত্রচুম্বক বলা হয়। তবে ক্ষেত্রচুম্বক হিসেবে সাধারণত স্থায়ী চুম্বকের পরিবর্তে তড়িৎচুম্বক ব্যবহার করা হয়। এই ক্ষেত্রচুম্বক, মেরু দুটির মাঝে উত্তর মেরু থেকে দক্ষিণ মেরুর দিকে প্রায় সুষম চৌম্বক ক্ষেত্র উৎপন্ন করে। ABCD হল চৌম্বক ক্ষেত্রে রাখা একটি আয়তাকার তার কুণ্ডলী। একটি নরম লোহার চোঙের ওপর অন্তরিত তামার তার জড়িয়ে এই কুণ্ডলী গঠন করা হয়। একে আর্মেচার বলা হয়। ABCD কুণ্ডলীর খোলা প্রান্ত দুটি যথাক্রমে দুটি পিতলের মসৃণ গোলাকার রিং R1 ও R2 -এর সঙ্গে যুক্ত থাকে। এই রিং দুটি কুণ্ডলীর ঘূর্ণনের সঙ্গে ঘোরে। B1 ও B2 হল দুটি কার্বন নির্মিত ব্রাশ। যখন ABCD কুণ্ডলী রিং-সহ ঘোরে তখন ব্রাশগুলি আলগাভাবে রিং দুটিকে স্পর্শ করে থাকে। B1 ও B2 ব্রাশের সঙ্গে বহির্বর্তনীতে R রোধ যুক্ত করা হয়। এবার ABCD কুণ্ডলীকে ঘোরালে কুণ্ডলীর সঙ্গে জড়িত চৗম্বক প্রবাহের পরিবর্তন হয়। ফলে কুণ্ডলীতে তড়িৎচালক বলের আবেশ ঘটে এবং বর্তনীতে তড়িৎপ্রবাহ চলে। ABCD কুণ্ডলীর AB বাহু যখন নীচের দিকে নামে তখন R রোধে তড়িৎপ্রবাহ যে অভিমুখে হয়, AB বাহু যখন ওপর দিকে ওঠে তখন R রোধে তড়িৎপ্রবাহ বিপরীত দিকে হয়। অর্থাৎ ABCD কুণ্ডলীর একবার পূর্ণ আবর্তনে R রোধে তড়িৎপ্রবাহের অভিমুখের দু-বার পরিবর্তন ঘটে। এইভাবে ABCD কুণ্ডলী সমকৌণিক বেগে ঘুরতে থাকলে R রোধে তড়িৎপ্রবাহের অভিমুখ নির্দিষ্ট সময় অন্তর পর্যায়ক্রমে বিপরীত হয় এবং উৎপন্ন তড়িৎপ্রবাহ ac হয়।
একটি dc ডায়নামোর কার্যনীতির সংক্ষিপ্ত আলোচনা করো।
নীচের চিত্রে একটি dc ডায়নামোর মূল অংশ দেখানো হয়েছে। এর মূল অংশগুলি হল – ক্ষেত্রচুম্বক, আর্মেচার, কম্যুটেটর ও ব্রাশ। N ও S হল একটি অশ্বক্ষুরাকৃতি চুম্বকের দুটি মেরু, এটিকে ক্ষেত্রচুম্বক বলা হয়। তবে ক্ষেত্রচুম্বক হিসেবে সাধারণত স্থায়ী চুম্বকের পরিবর্তে তড়িৎচুম্বক ব্যবহার করা হয়। এই ক্ষেত্রচুম্বক, মেরু দুটির মাঝে উত্তর মেরু থেকে দক্ষিণ মেরুর দিকে প্রায় সুষম চৌম্বক ক্ষেত্র উৎপন্ন করে। ABCD হল চৌম্বক ক্ষেত্রে রাখা একটি আয়তাকার তার কুণ্ডলী। একটি নরম লোহার চোঙের ওপর অন্তরিত তামার তার জড়িয়ে এই কুণ্ডলী গঠন করা হয়। একে আর্মেচার বলা হয়। এই ABCD কুণ্ডলীর খোলা প্রান্ত দুটি যথাক্রমে পিতলের তৈরি দুটি অর্ধচোঙাকৃতি পাত R1 ও R2 -এর সঙ্গে যুক্ত থাকে। R1 ও R2 -কে একত্রে কম্যুটেটর বলা হয়। কুণ্ডলী ঘুরলে তার সঙ্গে কম্যুটেটরও ঘোরে। B1 ও B2 হল দুটি কার্বন নির্মিত ব্রাশ। যখন ABCD কুণ্ডলী কম্যুটেটরসহ ঘোরে তখন ব্রাশগুলি কম্যুটেটরের দুটি পাতের সঙ্গে আলগাভাবে স্পর্শ করে থাকে। B1 ও B2 ব্রাশের সঙ্গে বহির্বর্তনীতে R রোধ যুক্ত করা হয়। এবার কুণ্ডলীটি ঘুরতে থাকলে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হয়। ফলে কুণ্ডলীতে তড়িৎচালক বলের আবেশ ঘটে এবং বর্তনীতে তড়িৎপ্রবাহ চলে। কুণ্ডলীটি ঘুরতে ঘুরতে যখন খাড়া হয় তখন AB বাহু নীচে ও CD বাহু ওপরে থাকে। তখন গতিজাড্যের জন্য AB বাহু ওপরের দিকে ও CD বাহু নীচের দিকে নামতে চায়। তখন R1 পাত, B2 ব্রাশের সঙ্গে ও R2 পাত, B1 ব্রাশের সংস্পর্শে আসে। ফলে প্রবাহমাত্রা বিপরীতমুখী না হয়ে একমুখী হয় এবং বহির্বর্তনীতে R রোধের মধ্য দিয়ে একই দিকে তড়িৎপ্রবাহ হয় অর্থাৎ dc উৎপন্ন হয়।
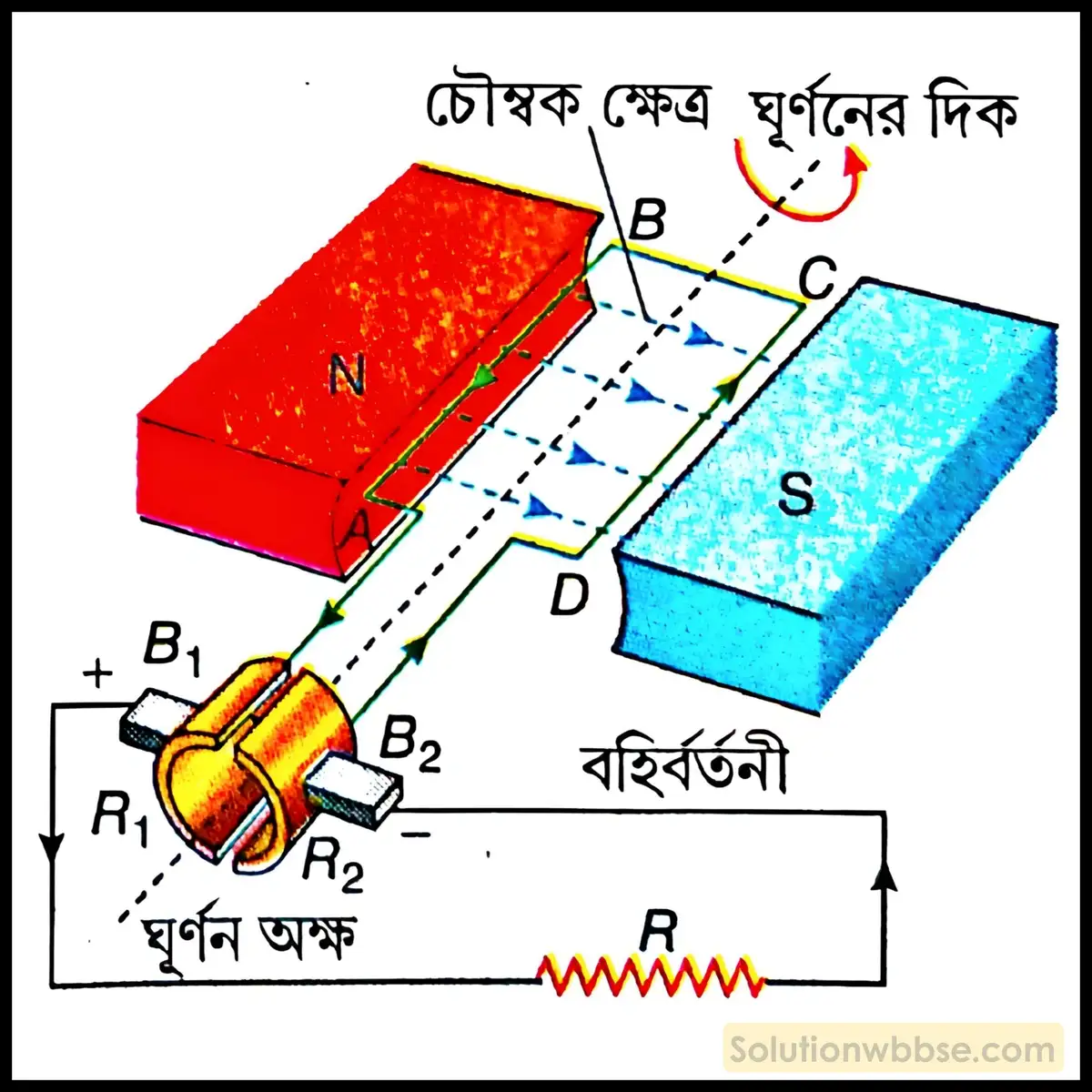
ডায়নামোতে উৎপন্ন তড়িৎচালক বল কিসের সঙ্গে সমানুপাতিক?
ডায়নামোতে উৎপন্ন তড়িৎচালক বল কুণ্ডলীর পাকসংখ্যা, কুণ্ডলীর আবর্তন বেগ, কুণ্ডলীর তলের ক্ষেত্রফল ও চৌম্বক ক্ষেত্রের প্রাবল্যের সমানুপাতিক।
একটি ডায়নামো ও একটি বৈদ্যুতিক মোটরের মধ্যে পার্থক্য লেখো।
ডায়নামো ও বৈদ্যুতিক মোটরের মধ্যে পার্থক্য –
| ডায়নামো | বৈদ্যুতিক মোটর |
| 1. ডায়নামোতে যান্ত্রিক শক্তি, তড়িৎশক্তিতে রূপান্তরিত হয়। | 1. বৈদ্যুতিক মোটরে তড়িৎ-শক্তি, যান্ত্রিক শক্তিতে রূপান্তরিত হয়। |
| 2. ডায়নামো তড়িৎচুম্বকীয় আবেশের নীতির ভিত্তিতে গঠিত। | 2. বৈদ্যুতিক মোটর তড়িৎপ্রবাহের চৌম্বক ক্রিয়ার ভিত্তিতে গঠিত। |
তাপবিদ্যুৎ উৎপন্নের কৌশলের সংক্ষিপ্ত আলোচনা করো।
ডায়নামোর কুণ্ডলীর সঙ্গে একটি দণ্ড যুক্ত থাকে যার প্রান্তে কতকগুলি ব্লেড থাকে, এটিকে টারবাইন বলা হয়। টারবাইনকে ঘোরালে কুণ্ডলীটি ঘোরে এবং তড়িৎশক্তি উৎপন্ন হয়।
তাপবিদ্যুৎ কেন্দ্রে কয়লা বা অন্য কোনো জ্বালানীর সাহায্যে জল ফুটিয়ে স্টিমে রূপান্তরিত করা হয়। এই স্টিম টারবাইনের ব্লেডকে ঘোরায় এবং ডায়নামোর আর্মেচার কুণ্ডলী ঘোরে। ফলে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হয় ও তড়িৎচালক বল আবিষ্ট হয় এবং উৎপন্ন হয় তাপবিদ্যুৎ। এই স্টিমকে আবার কনডেনসারে ঘনীভূত করা হয় এবং যেখানে এটি উত্তপ্ত হচ্ছে সেখানে আবার পাঠানো হয় র্যানকিন চক্রের দ্বারা।
জলবিদ্যুৎ উৎপন্নের কৌশলের সংক্ষিপ্ত আলোচনা করো।
ডায়নামোর কুণ্ডলীর সঙ্গে একটি দণ্ড যুক্ত থাকে যার প্রান্তে কতকগুলি ব্লেড থাকে, এটিকে টারবাইন বলা হয়। টারবাইনকে ঘোরালে কুণ্ডলীটি ঘোরে এবং তড়িৎশক্তি উৎপন্ন হয়।
জলবিদ্যুৎ কেন্দ্রে জলাধারে জলকে সঞ্চয় করে রাখা হয়। এবার অনেক উঁচুতে থাকা জলাধারের জলকে নীচে ফেলা হয়। নীচে পড়ার জন্য জলের স্থিতিশক্তির হ্রাস পায় এবং গতিশক্তি বৃদ্ধি পায়। এই গতিশীল জলে টারবাইনের ব্লেড রাখলে তা ঘোরে এবং ডায়নামোর আর্মেচার কুণ্ডলীকে ঘোরায়। ফলে কুণ্ডলীর সঙ্গে জড়িত চৌম্বক প্রবাহের পরিবর্তন হয়। ফলে তড়িৎচালক বল আবিষ্ট হয় এবং উৎপন্ন হয় জলবিদ্যুৎ।
পৃথিবীর অনেক দেশ জলবিদ্যুৎ উৎপাদনের দিকে গুরুত্ব দিচ্ছে কেন?
তাপবিদ্যুৎ উৎপাদন কেন্দ্রে প্রচুর পরিমাণে CO2 উৎপন্ন হয় যা পরিবেশ দূষণ ঘটায়। এজন্য পৃথিবীর অনেক দেশ জলবিদ্যুৎ উৎপাদনের দিকে গুরুত্ব দিচ্ছে। বর্তমানে পৃথিবীর উৎপন্ন তড়িৎশক্তির প্রায় 16% হল জলবিদ্যুৎ।
বাড়িতে বৈদ্যুতিক লাইনে বাতি, বৈদ্যুতিক পাখা, রেফ্রিজারেটর ইত্যাদি কোন্ সমবায়ে যুক্ত থাকে ও কেন?
বাড়িতে বৈদ্যুতিক লাইনে বাতি, বৈদ্যুতিক পাখা, রেফ্রিজারেটর ইত্যাদি সব সমান্তরাল সমবায়ে থাকে, কারণ প্রয়োজনমতো যে-কোনো একটি অন বা অফ করা যায় এবং প্রত্যেকটি তড়িৎযন্ত্রের দু-প্রান্তের বিভবপ্রভেদ স্থির থাকে।
বাড়িতে বৈদ্যুতিক লাইন ব্যবস্থা চিত্রসহ বুঝিয়ে দাও।
বাড়িতে বিদ্যুৎ সরবরাহের জন্য বিদ্যুৎ সরবরাহ সংস্থার ওভারহেড বা আন্ডারগ্রাউন্ড কেবল থেকে বাড়িতে দুটি তার টানা হয়। একটি হল লাইভ তার, অন্যটি নিউট্রাল তার। সাধারণত লাইভ তারে লাল প্লাস্টিকের আবরণ ও নিউট্রাল তারে কালো প্লাস্টিকের আবরণ দেওয়া থাকে। বর্তমানে আন্তর্জাতিক নিয়ম অনুযায়ী, লাইভ তারটি বাদামি ও নিউট্রাল তারটি হালকা নীল (বা আকাশি) রঙের প্লাস্টিকের আবরণ দেওয়া হয়।
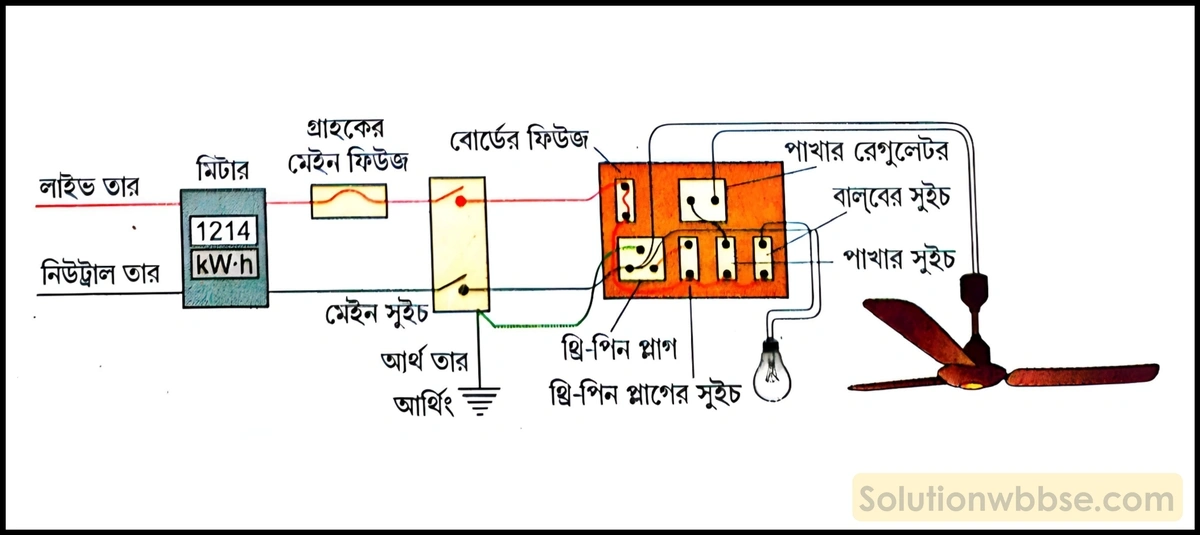
লাইভ তার ও নিউটাল তারকে প্রথমে মিটারের সঙ্গে যুক্ত করা হয়। এবার মেইন ফিউজের মধ্যে দিয়ে লাইভ তারকে এবং মিটার থেকে সরাসরি নিউট্রাল তারকে মেইন সুইচের সঙ্গে যুক্ত করা হয়। মেইন সুইচের সাহায্যে বাড়ির লাইনকে প্রয়োজনমতো অন বা অফ করা যায়। ভূমি ও নিউট্রাল তারের মধ্যে বিভবপ্রভেদ সর্বদা শূন্য না হওয়ায় একটি লোহার রডকে ভূমিতে প্রবেশ করিয়ে ওই রডের সঙ্গে পরিবাহী তার যোগ করা হয়। এই ব্যবস্থাকে আর্থিং বলা হয় এবং ব্যবহৃত তারটিকে আর্থ তার বলা হয়। আর্থ তারটি সবুজ বা হলুদ রঙের হয়। আর্থ তারকে মেইন সুইচের মধ্য দিয়ে বৈদ্যুতিক যন্ত্রের (ইস্ত্রি, রেফ্রিজারেটর, টেবিল ফ্যান ইত্যদি) জন্য যে সুইচ বোর্ড তাতে নিয়ে যাওয়া হয়। মেইন সুইচ থেকে লাইভ তার কতকগুলি শাখা লাইনের মাধ্যমে বিভিন্ন সুইচ বোর্ডে যায়। সুইচ বোর্ডে বৈদ্যুতিক পাখা, টিভি, বাতি ইত্যাদি ব্যবহারের জন্য প্রয়োজনমতো পয়েন্ট করা হয়। প্রতিটি সুইচ বোর্ডে লাইভ তারটি একটি ফিউজের মধ্য দিয়ে যায়। এবার সুইচ বোর্ড থেকে লাইভ তার ও নিউট্রাল তারের মাধ্যমে বাড়ির ওয়্যারিং করা হয়। বাড়িতে বাতি, রেফ্রিজারেটর, বৈদ্যুতিক পাখা ইত্যাদি সব সমান্তরাল সমবায়ে থাকে।
বাড়িতে বৈদ্যুতিক লাইনে আর্থিং কেন করা হয়?
ভূমি ও নিউট্রাল তারের মধ্যে বিভবপ্রভেদ সর্বদা শূন্য না হওয়ায় একটি লোহার রডকে ভূমিতে প্রবেশ করিয়ে ওই রডের সঙ্গে পরিবাহী তার যোগ করা হয়। এই ব্যবস্থাকে আর্থিং বলা হয়। বাড়ির লাইনকে শট-সার্কিটের বিপদ থেকে রক্ষা করে আর্থিং। এ ছাড়া ইস্ত্রি, রেফ্রিজারেটর, টেবিল ফ্যান ইত্যাদি বৈদ্যুতিক যন্ত্রের ধাতব আবরণ কোনো কারণে লাইভ তারের সংস্পর্শে এলে সেই তড়িৎশক্তি আর্থ তারের মাধ্যমে ভূমিতে চলে যায় এবং বিপদের সম্ভাবনা অনেক কমে যায়।
সুইচ ও মেইন সুইচের কার্য ব্যাখ্যা করো।
সুইচ – সুইচ হল তড়িৎবর্তনীতে এমন একটি ব্যবস্থা যার দ্বারা তড়িৎবর্তনীতে তড়িৎপ্রবাহ অন বা অফ করা যায়। সুইচ সাধারণত এবোনাইটের তৈরি হয় এবং দেয়ালের গায়ে সংশ্লিষ্ট বোর্ডে লাগানো হয়। সাধারণত বৈদ্যুতিক পাখা, বাল্ব, টিউবলাইট -এর বর্তনীতে 5 A সুইচ ও রেফ্রিজারেটর, পাম্প, হিটার -এর বর্তনীতে 10 A বা 15 A -এর সুইচ ব্যবহার করা হয়।

মেইন সুইচ – মেইন সুইচ এমন একটি ব্যবস্থা যাকে প্রয়োজনমতো অন বা অফ করে বাড়ির বৈদ্যুতিক লাইনকে বিদ্যুৎ সরবরাহ লাইনের সঙ্গে যথাক্রমে সংযুক্ত বা বিচ্ছিন্ন করা যায়। ফলে বাড়িতে ইচ্ছামতো তড়িৎপ্রবাহ চালু বা বন্ধ করা যায়।

থ্রি-পিন প্লাগ ও সকেটের কার্য ব্যাখ্যা করো।
টিভি, রেফ্রিজারেটর, হিটার, মিক্সার প্রভৃতি তড়িৎযন্ত্রকে প্লাগের সাহায্যে সকেটে আটকে তড়িৎ সংযোগ করা হয়। সকেটে তিনটি ছিদ্র থাকে এবং ছিদ্রের প্রায় অর্ধেক অংশে ধাতব আবরণ থাকে। এই তিনটি ছিদ্রের নীচের দুটির সঙ্গে লাইভ তার ও নিউট্রাল তার এবং ওপরের অপেক্ষাকৃত বড়ো ছিদ্রটির সঙ্গে আর্থ তার যুক্ত থাকে। সকেট সংশ্লিষ্ট বোর্ডের সঙ্গে যুক্ত থাকে। থ্রি-পিন প্লাগে তিনটি পিন থাকে। এই তিনটি পিনের ওপরের একটি পিন বাকি দুটি সমান পিনের চেয়ে একটু মোটা ও লম্বা হয়। সমান দুটি পিনের একটি লাইভ তারের সঙ্গে ও অন্যটি নিউট্রাল তারের সঙ্গে যুক্ত। মোটা পিনের সঙ্গে আর্থের সংযোগ করা হয়। আর্থ পিনটি মোটা করা হয় যাতে ভুলবশত এটিকে অন্য দুটি ছিদ্রে প্রবেশ করানো না যায়। আবার আর্থ পিনটি লম্বা করা হয়, যাতে লাইভ পিন বা নিউট্রাল পিন অপেক্ষা এই পিনটির প্রান্ত, সকেটের সঙ্গে আগে যুক্ত হয় এবং ব্যবহারকারীর শক্ খাওয়ার সম্ভাবনা কম হয়। থ্রি-পিন প্লাগে প্রতিটি পিনের সম্মুখভাগ লম্বালম্বিভাবে চেরা থাকে, যাতে সকেটে সংযোগ আলগা হয়ে গেলে একটু টেনে ভালোভাবে সংযোগ স্থাপন করা যায়, না হলে সংযোগ আলগা হয়ে স্ফুলিঙ্গ হতে পারে যা বিপজ্জনক।

Class 10 Physical Science – Notes for All Chapters
আমরা আমাদের আর্টিকেলে দশম শ্রেণীর ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় ‘চলতড়িৎ’ এর সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর নিয়ে আলোচনা করেছি। এই প্রশ্নগুলো দশম শ্রেণীর ভৌতবিজ্ঞান পরীক্ষার জন্য বা চাকরির পরীক্ষার জন্য অনেক গুরুত্বপূর্ণ। কারণ এই প্রশ্নগুলি দশম শ্রেণীর পরীক্ষা বা চাকরির পরীক্ষায় প্রায় দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা হলে, আপনারা আমাদের সাথে টেলিগ্রামে যোগাযোগ করতে পারেন, আমরা উত্তর দেওয়ার চেষ্টা করবো। তাছাড়া নিচে আমাদের এই পোস্টটি আপনার প্রিয়জনের সাথে শেয়ার করুন, যাদের এটি প্রয়োজন হতে পারে। ধন্যবাদ।






মন্তব্য করুন