মাধ্যমিক ভৌতবিজ্ঞান – আলো – সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর

আমরা আমাদের আর্টিকেলে দশম শ্রেণীর ভৌতবিজ্ঞানের পঞ্চম অধ্যায় ‘আলো’ এর কিছু সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর নিয়ে আলোচনা করবো। এই প্রশ্নগুলো দশম শ্রেণীর ভৌতবিজ্ঞান পরীক্ষার জন্য ও চাকরির পরীক্ষার জন্য অনেক গুরুত্বপূর্ণ।

আলোর প্রতিফলক হিসেবে গোলীয় দর্পণ

একটি চকচকে চামচের অবতল ও উত্তল দিকের সামনে মুখ রাখলে কী দেখা যাবে?

একটি চকচকে চামচের অবতল দিকের খুব সামনে মুখ রাখলে মুখের বিবর্ধিত, সমশীর্ষ প্রতিবিম্ব চামচে দেখা যাবে। এবার চামচ থেকে দূরে সরে গেলে প্রতিবিম্ব অবশীর্ষ ও খর্বকায় হয়। আবার চামচের উত্তল দিকের কাছে মুখ রাখলে সমশীর্ষ ও খর্বকায় প্রতিবিম্ব দেখা যাবে।

গোলীয় দর্পণ কাকে বলে? গোলীয় দর্পণ কয় প্রকার ও কী কী?

কোনো প্রতিফলক তল যদি কোনো গোলকের অংশবিশেষ হয় তবে তাকে গোলীয় দর্পণ বলা হয়। গোলীয় দর্পণ দু-ধরনের হতে পারে –

1. অবতল দর্পণ ও
2. উত্তল দর্পণ।

উত্তল দর্পণ ও অবতল দর্পণ কাকে বলে?

উত্তল দর্পণ – যে গোলীয় দর্পণের বাইরের উত্তল তল, প্রতিফলক হিসেবে কাজ করে তাকে উত্তল দর্পণ বলা হয়।

অবতল দর্পণ – যে গোলীয় দর্পণের ভিতরের অবতল তল, প্রতিফলক হিসেবে কাজ করে তাকে অবতল দর্পণ বলা হয়।

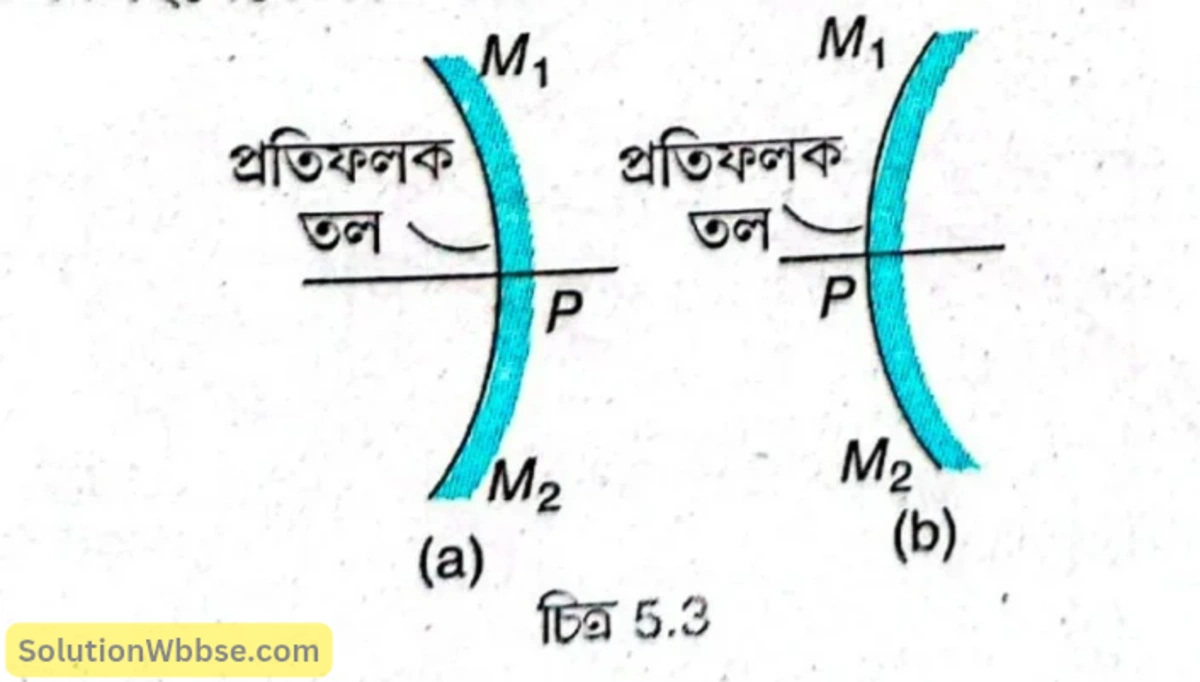
গোলীয় দর্পণের মেরু, বক্রতা কেন্দ্র, বক্রতা ব্যাসার্ধ, প্রধান অক্ষ ও প্রধান ছেদের সংজ্ঞা লেখো এবং চিত্রে চিহ্নিত করো।

মেরু – কোনো গোলীয় দর্পণের মধ্যবিন্দুকে মেরু বলা হয়।

বক্রতা কেন্দ্র – কোনো গোলীয় দর্পণ যে গোলকের অংশ তার কেন্দ্রকে বক্রতা কেন্দ্র বলা হয়।

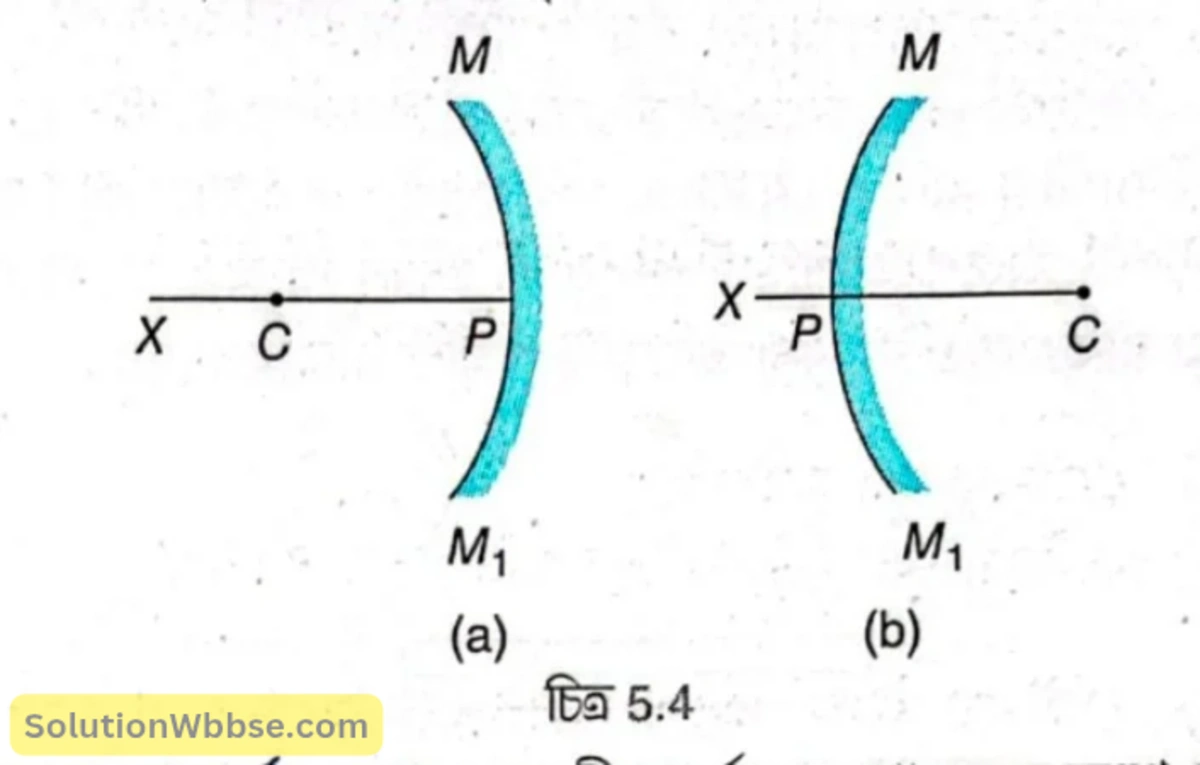
বক্রতা ব্যাসার্ধ – কোনো গোলীয় দর্পণ যে গোলকের অংশ সেই গোলকের ব্যাসার্ধকে ওই গোলীয় দর্পণের বক্রতা ব্যাসার্ধ বলা হয়।

প্রধান অক্ষ – কোনো গোলীয় দর্পণের মেরু ও বক্রতা কেন্দ্রগামী সরলরেখাকে প্রধান অক্ষ বলা হয়।

প্রধান ছেদ – কোনো গোলীয় দর্পণের প্রধান অক্ষের মধ্য দিয়ে কোনো সমতল কল্পনা করা হলে সেটি গোলীয় দর্পণকে একটি বৃত্তচাপে ছেদ করে, তাকে ওই গোলীয় দর্পণের প্রধান ছেদ বলা হয়।

5.4 (a) ও (b) নং চিত্রে MPM₁ হল যথাক্রমে একটি অবতল ও একটি উত্তল দর্পণের প্রধান ছেদ। যেখানে P হল মেরু, C হল বক্রতা কেন্দ্র, PC হল বক্রতা ব্যাসার্ধ এবং PX হল প্রধান অক্ষ।

গোলীয় দর্পণের রৈখিক উন্মেষ ও কৌণিক উন্মেষের চিত্রসহ সংজ্ঞা লেখো।

রৈখিক উন্মেষ – কোনো গোলীয় দর্পণের পরিসীমা বৃত্তাকার। এই বৃত্তের ব্যাসকে গোলীয় দর্পণের রৈখিক উন্মেষ বলা হয়।

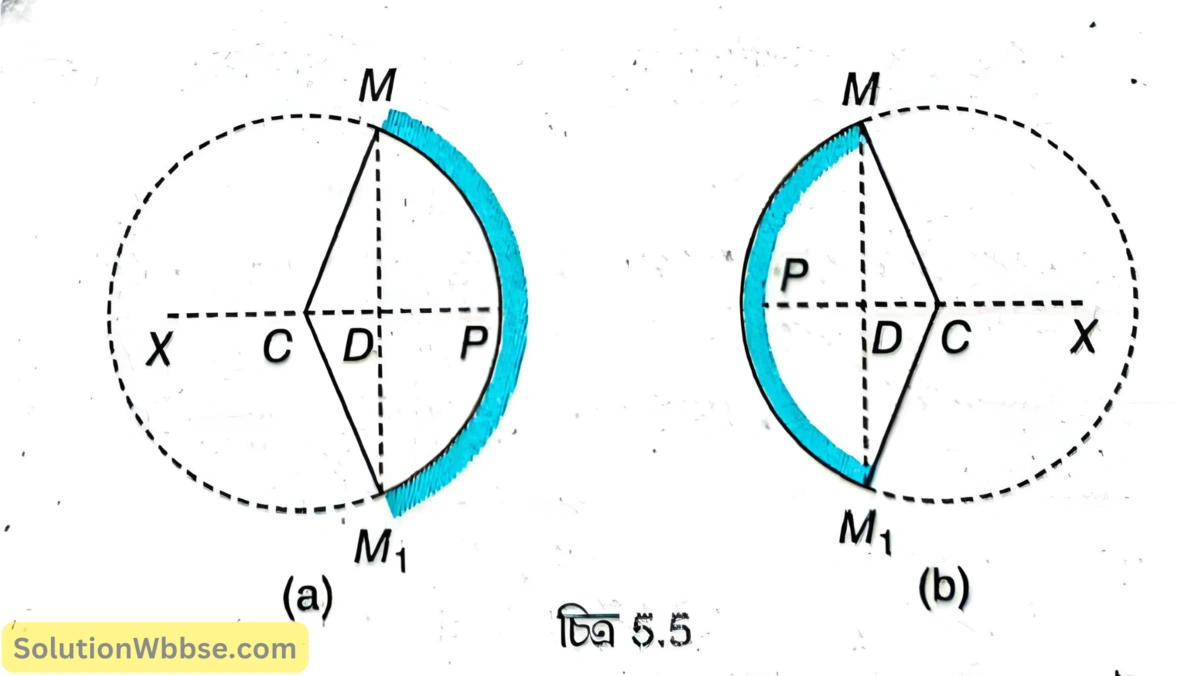
5.5 (a) ও (b) নম্বর চিত্রে MM₁ হল যথাক্রমে অবতল ও উত্তল দর্পণের বৃত্তাকার পরিসীমার ব্যাস, তাই MM₁ হল রৈখিক উন্মেষ।

কৌণিক উন্মেষ – কোনো গোলীয় দর্পণের প্রধান ছেদের দুটি প্রান্তবিন্দু বক্রতা কেন্দ্রে যে কোণ উৎপন্ন করে তাকে কৌণিক উন্মেষ বলা হয়।

5.5 (a) ও (b) নম্বর চিত্রে MPM₁ হল যথাক্রমে অবতল ও উত্তল দর্পণের প্রধান ছেদ। প্রধান ছেদের দুটি প্রান্তবিন্দু M ও M₁ বক্রতা কেন্দ্রে ∠MCM₁ কোণ উৎপন্ন করে। ∠MCM₁ হল কৌণিক উন্মেষ।

উপাক্ষীয় রশ্মি কাকে বলে? চিত্রের সাহায্যে দেখাও।

উপাক্ষীয় রশ্মি – যে সমস্ত রশ্মি গোলীয় দর্পণের মেরুর খুব নিকটবর্তী অংশে আপতিত হয় এবং প্রধান অক্ষের সঙ্গে যে সমস্ত রশ্মির নতি খুব কম তাদের উপাক্ষীয় রশ্মি বলা হয়।

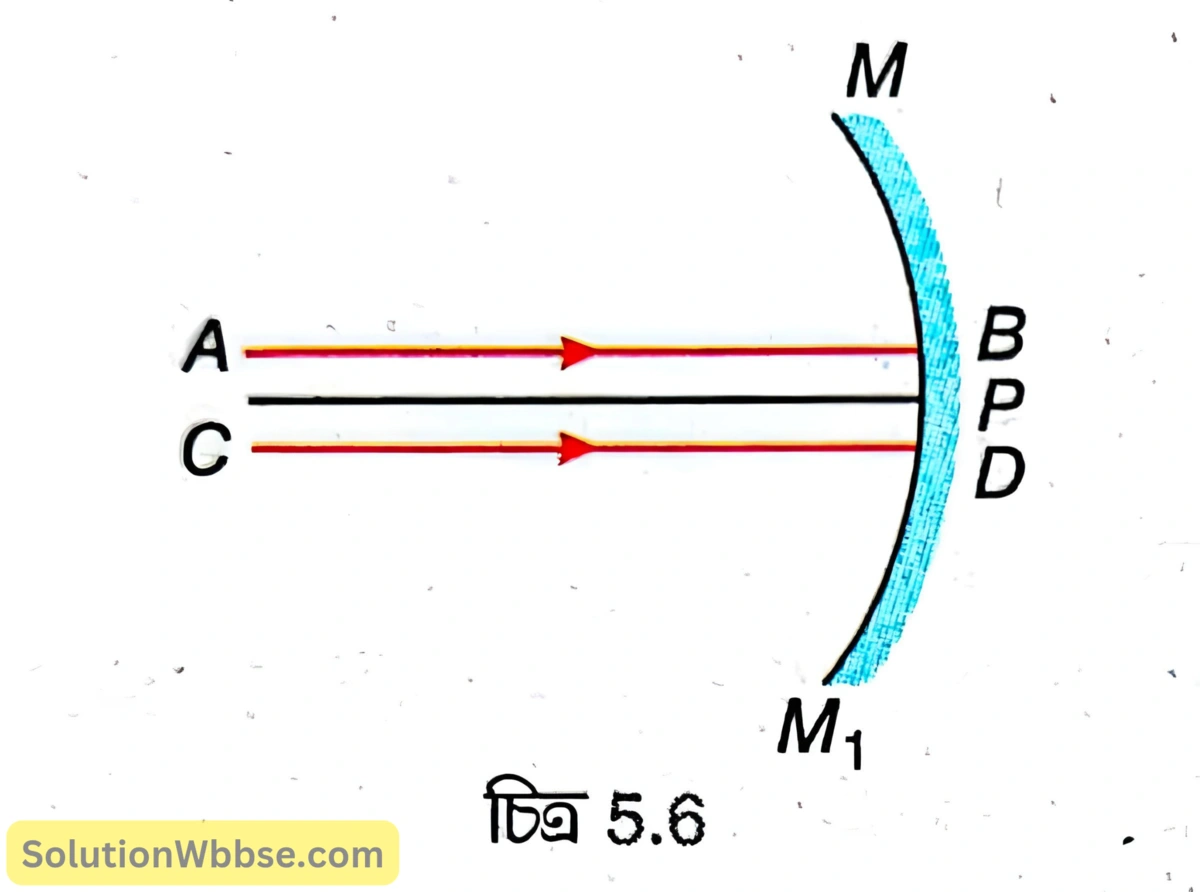
5.6 নম্বর চিত্রে MPM₁ হল একটি অবতল দর্পণের প্রধান ছেদ যার P হল মেরু। AB ও CD রশ্মি দুটি মেরুর খুব নিকটবর্তী অঞ্চলে আপতিত হয়েছে এবং প্রধান অক্ষের সঙ্গে রশ্মি দুটির নতি খুব কম। তাই AB ও CD হল উপাক্ষীয় রশ্মি।

অবতল দর্পণ ও উত্তল দর্পণের মুখ্য ফোকাস কাকে বলে? রশ্মিচিত্রের সাহায্যে উভয় দর্পণের মুখ্য ফোকাস দেখাও।

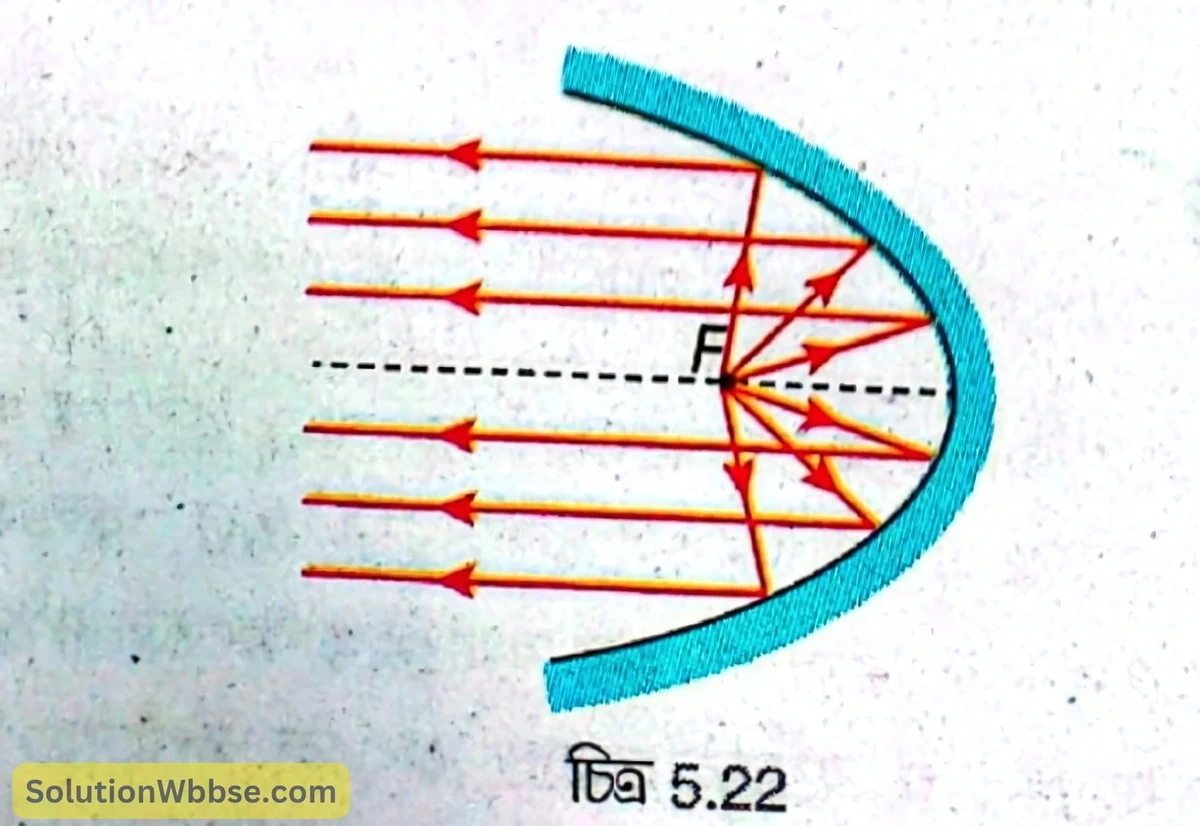
অবতল দর্পণের মুখ্য ফোকাস – ক্ষুদ্র উন্মেষযুক্ত কোনো অবতল দর্পণের প্রধান অক্ষের সঙ্গে সমান্তরালভাবে আপতিত সমান্তরাল রশ্মিগুচ্ছ, দর্পণ দ্বারা প্রতিফলনের পর প্রধান অক্ষের ওপর একটি বিন্দুতে মিলিত হয়, সেই নির্দিষ্ট বিন্দুটিকে অবতল দর্পণের মুখ্য ফোকাস বলা হয়।

উত্তল দর্পণের মুখ্য ফোকাস – ক্ষুদ্র উন্মেষযুক্ত কোনো উত্তল দর্পণের প্রধান অক্ষের সঙ্গে সমান্তরালভাবে আপতিত সমান্তরাল রশ্মিগুচ্ছ, দর্পণ দ্বারা প্রতিফলনের পর, প্রধান অক্ষের ওপর একটি বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়, সেই নির্দিষ্ট বিন্দুটিকে উত্তল দর্পণের মুখ্য ফোকাস বলা হয়।

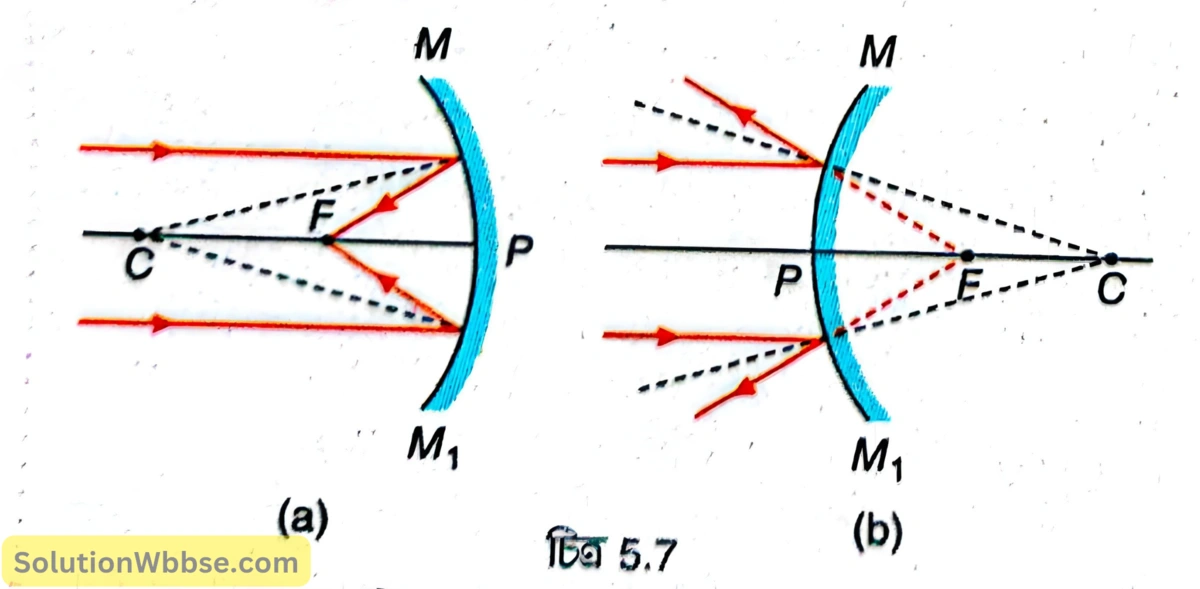
5.7 (a) ও (b) নম্বর চিত্রে যথাক্রমে অবতল ও উত্তল দর্পণের প্রধান অক্ষের সমান্তরাল রশ্মিগুচ্ছের প্রতিফলন দেখানো হয়েছে। প্রতিটি আপতিত রশ্মির আপতন বিন্দুর সঙ্গে গোলীয় দর্পণের বক্রতা কেন্দ্র (C) ডট লাইন দ্বারা যুক্ত করা হয়েছে, যা ওই আপতন বিন্দুতে অভিলম্ব নির্দেশ করে। অবতল দর্পণের ক্ষেত্রে প্রতিফলিত রশ্মিগুচ্ছ প্রতিফলনের পর অভিসারী হয়ে প্রধান অক্ষের ওপর F বিন্দুতে মিলিত হয়। এই F –কে অবতল দর্পণের মুখ্য ফোকাস বলা হয়। আবার উত্তল দর্পণের ক্ষেত্রে প্রতিফলিত রশ্মিগুচ্ছ অপসারী হওয়ায় কোনো বিন্দুতে মিলিত হয় না, বরং দর্পণের পিছনে প্রধান অক্ষের ওপর একটি বিন্দু F থেকে অপসৃত হচ্ছে বলে মনে হয়। এই F বিন্দু হল উত্তল দর্পণের মুখ্য ফোকাস।

গোলীয় দর্পণের ফোকাস দূরত্ব ও ফোকাস তল কাকে বলে? চিত্রসহ দেখাও।

ফোকাস দূরত্ব – কোনো গোলীয় দর্পণের মেরু থেকে মুখ্য ফোকাসের দূরত্বই হল ফোকাস দূরত্ব।

ফোকাস তল – গোলীয় দর্পণের প্রধান অক্ষের সঙ্গে লম্ব ও মুখ্য ফোকাস বিন্দুগামী সমতলকে ফোকাস তল বলা হয়।

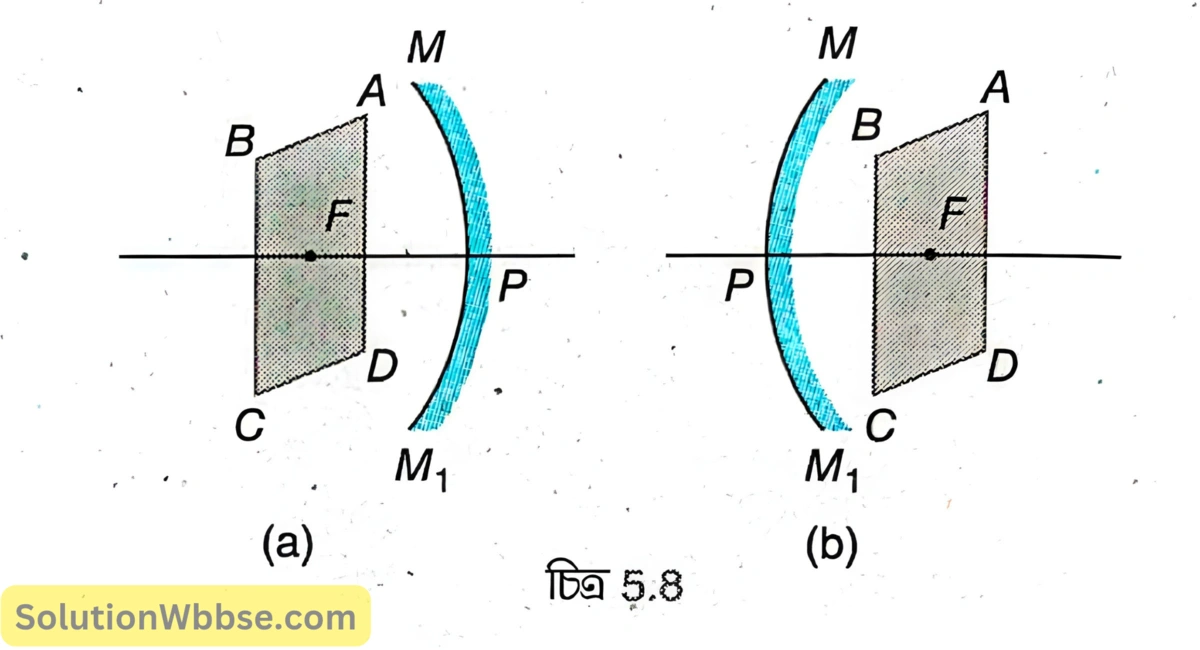
5.8 (a) ও (b) নম্বর চিত্রে MPM₁ হল যথাক্রমে একটি অবতল ও একটি উত্তল দর্পণের প্রধান ছেদ, যেখানে P হল মেরু ও F হল মুখ্য ফোকাস। PF হল ফোকাস দূরত্ব এবং ABCD হল ফোকাস তল।

গোলীয় দর্পণের গৌণ ফোকাস কাকে বলে? চিত্রসহ দেখাও।

গোলীয় দর্পণের গৌণ ফোকাস – গোলীয় দর্পণের প্রধান অক্ষের সঙ্গে আনতভাবে আপতিত সমান্তরাল রশ্মিগুচ্ছ, দর্পণ দ্বারা প্রতিফলনের পর অবতল দর্পণের ক্ষেত্রে ফোকাস তলের ওপর একটি বিন্দুতে মিলিত হয় এবং উত্তল দর্পণের ক্ষেত্রে ফোকাস তলের ওপর কোনো বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়, সেই বিন্দুকে ওই গোলীয় দর্পণের গৌণ ফোকাস বলা হয়।

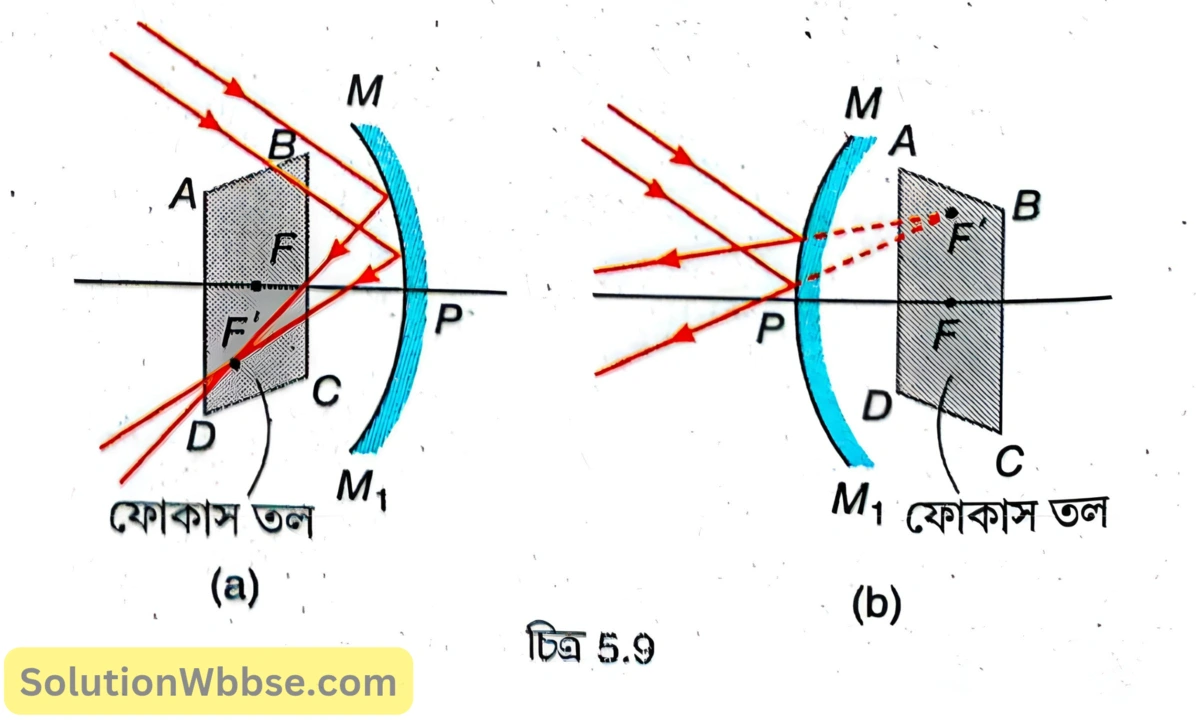
5.9 (a) ও (b) নম্বর চিত্রে MPM₁ হল যথাক্রমে একটি অবতল দর্পণ ও একটি উত্তল দর্পণের প্রধান ছেদ, যেখানে P হল মেরু, F হল মুখ্য ফোকাস ও ABCD হল ফোকাস তল এবং F’ হল গৌণ ফোকাস।

অবতল দর্পণের ক্ষেত্রে ফোকাস দূরত্ব ও বক্রতা ব্যাসার্ধের মধ্যে সম্পর্ক স্থাপন করো।

ক্ষুদ্র উন্মেষযুক্ত একটি অবতল দর্পণের MPM₁ হল প্রধান ছেদ। P, F ও C হল যথাক্রমে অবতল দর্পণের মেরু, মুখ্য ফোকাস ও বক্রতা কেন্দ্র। ফোকাস দূরত্ব, PF = f ও বক্রতা ব্যাসার্ধ, PC = r। অবতল দর্পণের প্রধান অক্ষের সঙ্গে সমান্তরালভাবে AB আলোকরশ্মি B বিন্দুতে দর্পণের ওপর আপতিত হয়ে প্রতিফলনের পর ফোকাসের (F) মধ্য দিয়ে যায়। C, B যুক্ত করা হল। CB হল B বিন্দুতে দর্পণের ওপর অভিলম্ব।

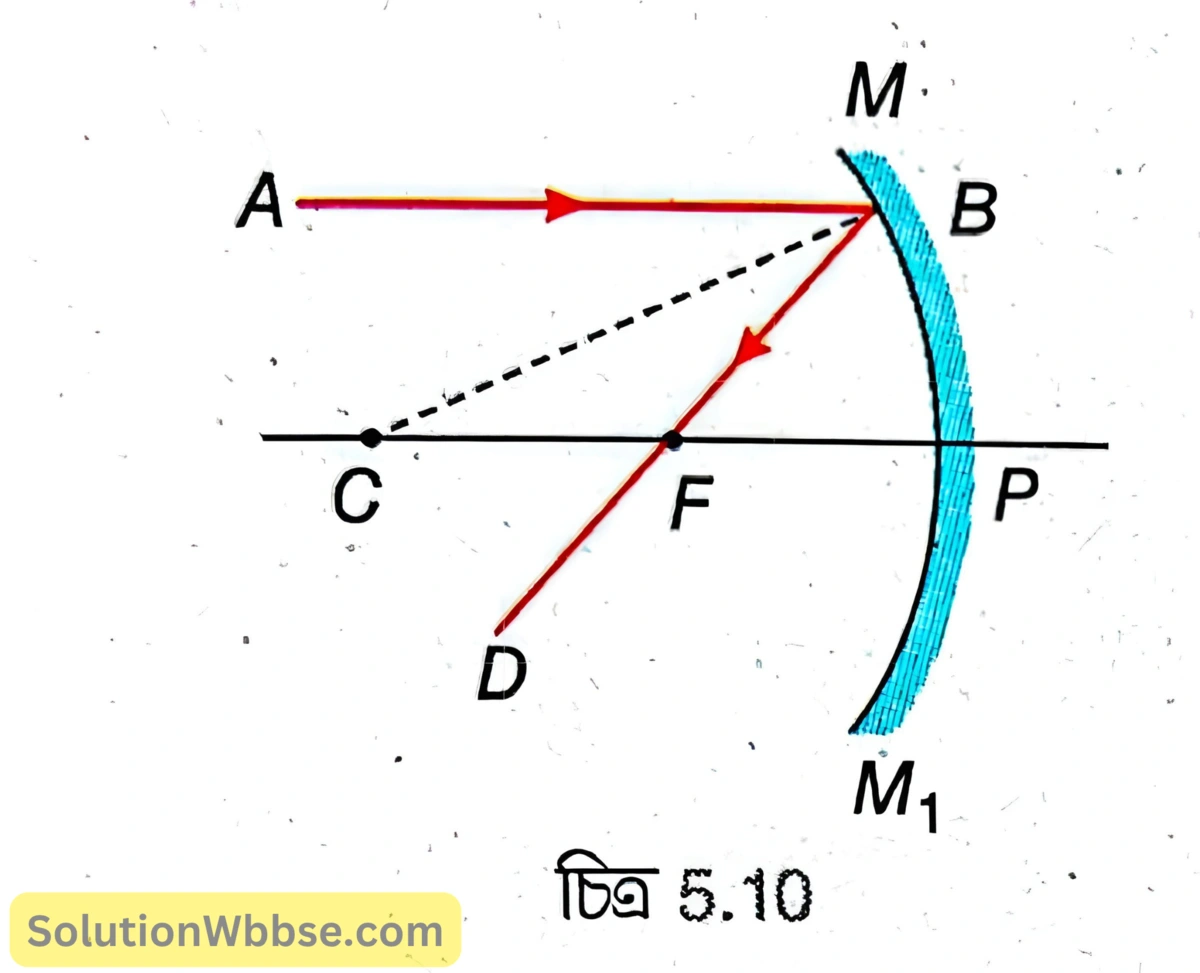
মনে করি, আপতন কোণ \(\angle ABC = \theta\)
∴ প্রতিফলন কোণ, \(\angle FBC = \theta\)
আবার, \( AB\parallel CP \) ও \( BC \) ভেদক।
∴ \(\angle ABC = \angle BCF\) [একান্তর কোণ]
∴ \(\angle BCF = \theta\)
∴ \(\Delta BCF\) –এর \(\angle FBC = \angle BCF\)।
∴ \(\Delta BCF\) সমদ্বিবাহু।
∴ \(CF = FB\)

যেহেতু দর্পণের উন্মেষ ক্ষুদ্র ও AB হল উপাক্ষীয় রশ্মি, সেহেতু B ও P বিন্দু দুটি খুবই নিকটবর্তী।

∴ \(FB \approx PF\)
অর্থাৎ, \(PF = CF\)
বা, \(PF = \frac{PC}{2}\)
অতএব, \(f = \frac{r}{2}\)

উত্তল দর্পণের ক্ষেত্রে ফোকাস দূরত্ব ও বক্রতা ব্যাসার্ধের মধ্যে সম্পর্ক স্থাপন করো।

ক্ষুদ্র উন্মেষযুক্ত একটি উত্তল দর্পণের MPM₁ হল প্রধান ছেদ। P, F ও C হল যথাক্রমে উত্তল দর্পণের মেরু, মুখ্য ফোকাস ও বক্রতা কেন্দ্র।

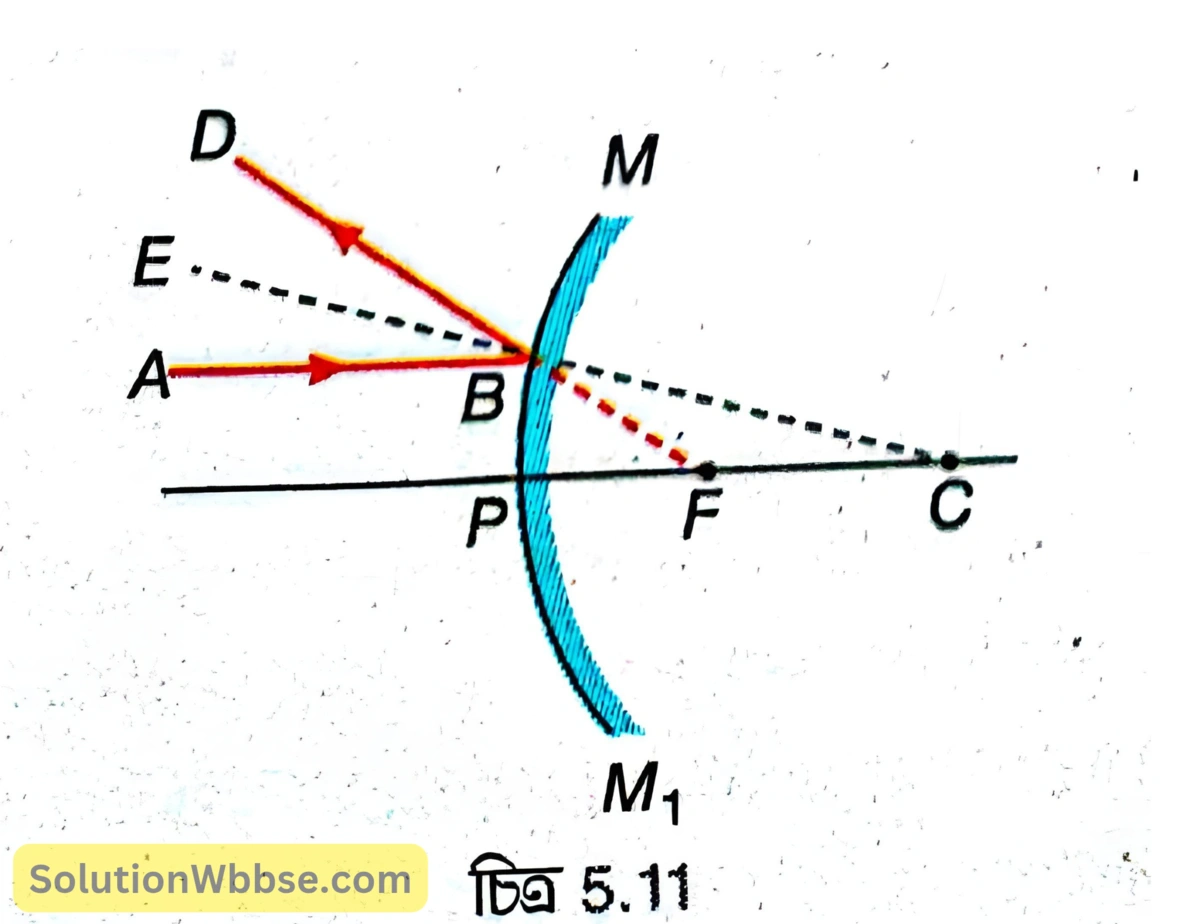
∴ ফোকাস দূরত্ব, PF = f ও বক্রতা ব্যাসার্ধ, PC = r। উত্তল দর্পণের প্রধান অক্ষের সঙ্গে সমান্তরালভাবে AB আলোকরশ্মি B বিন্দুতে আপতিত হয়ে BD পথে প্রতিফলিত হয়, মনে হয় যেন মুখ্য ফোকাস (F) থেকে অপসৃত হচ্ছে। C, B যুক্ত করে E পর্যন্ত বর্ধিত করা হল। CE হল B বিন্দুতে দর্পণের ওপর অভিলম্ব।

মনে করি, আপতন কোণ, \( \angle ABE=\theta \)
∴ প্রতিফলন কোণ, \(\angle DBE=\theta\)
আবার,\(AB\parallel PC \) ও \(EC \) ভেদক।
∴ \(\angle ABE=\angle FCB \) [অনুরূপে কোণ]
∴ \(\angle FCB=\theta \)
আবার, \(\angle FBC=\angle DBE\) [বিপ্রতীপ কোণ]
∴ \(\angle FBC=\theta \)
∴ \(\angle FBC=\angle FCB\)
∴ \(\bigtriangleup BCF\) সমদ্বিবাহু।
∴ \(FB=FC\)

যেহেতু দর্পণের উন্মেষ ক্ষুদ্র ও AB হল উপাক্ষীয় রশ্মি, সেহেতু B ও P বিন্দু দুটি খুবই নিকটবর্তী।

∴ \( FB\approx PF \)
অর্থাৎ, \(PF=FC \)
বা, \(PF=\frac{PC}2 \)
বা, \(f=\frac r2 \)

গোলীয় দর্পণে রশ্মি অণুসরণ পদ্ধতিটি লিখ?

গোলীয় দর্পণের সামনে থাকা কোনো বস্তুর কোনো বিন্দু থেকে বিভিন্ন দিকে অসংখ্য রশ্মি নির্গত হয়। কিন্তু প্রতিবিম্ব গঠনের জন্য যে-কোনো বিন্দু থেকে দুটি নির্গত রশ্মি নেওয়া হয়। নিম্নলিখিত চারটি রশ্মির মধ্য থেকে যে-কোনো দুটি রশ্মি বিবেচনা করা হয় –

• প্রধান অক্ষের সমান্তরালভাবে আপতিত রশ্মি,
• মুখ্য ফোকাসগামী বা মুখ্য ফোকাসের দিকে পরিচালিত আপতিত রশ্মি,
• বক্রতা কেন্দ্রগামী বা বক্রতা কেন্দ্রের দিকে পরিচালিত আপতিত রশ্মি ও
• গোলীয় দর্পণের মেরুতে আপতিত রশ্মি।

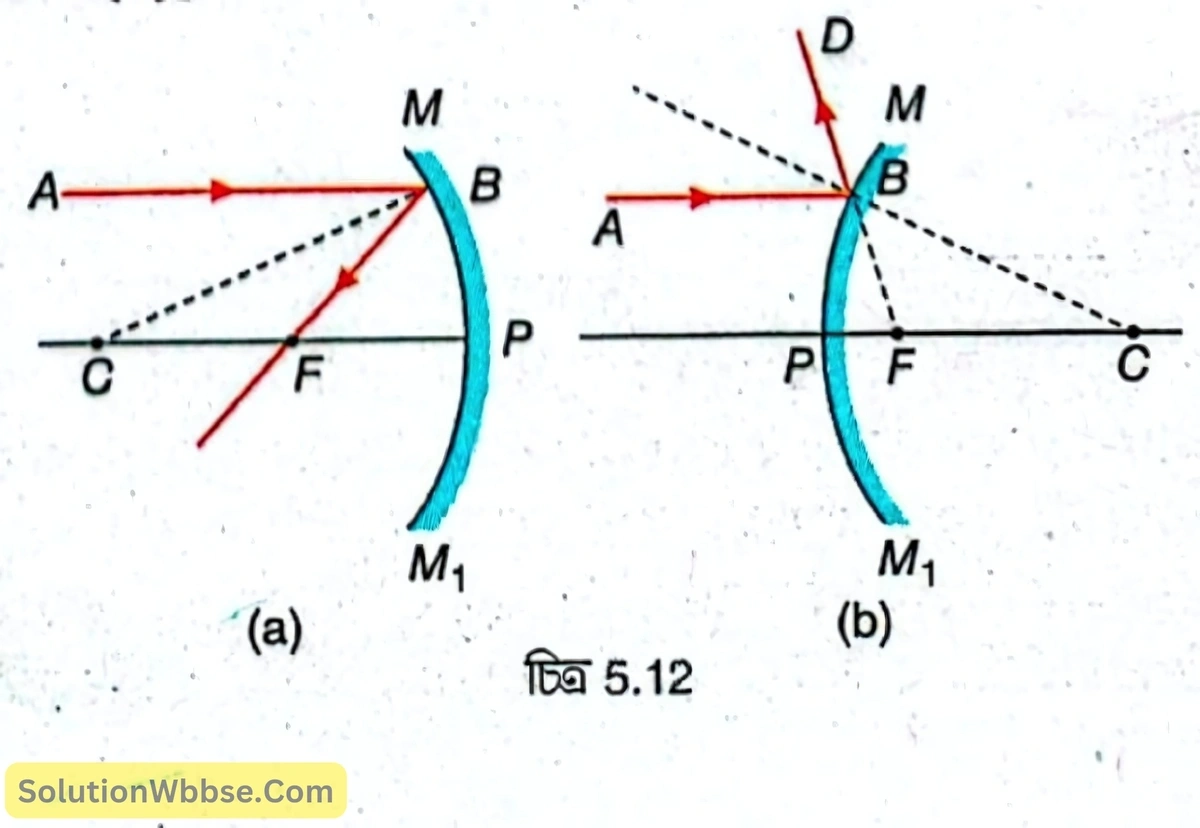
প্রধান অক্ষের সমান্তরালভাবে আপতিত রশ্মি – অবতল দর্পণের প্রধান অক্ষের সমান্তরাল রশ্মি AB, দর্পণ দ্বারা প্রতিফলনের পর মুখ্য ফোকাসের (F) মধ্য দিয়ে BD পথে যায় [চিত্র 5.12 (a)] এবং উত্তল দর্পণের প্রধান অক্ষের সমান্তরাল রশ্মি AB, দর্পণ দ্বারা প্রতিফলনের পর মুখ্য ফোকাস (F) থেকে অপসৃত হচ্ছে বলে মনে হয় [চিত্র 5.12 (b)] এবং BD পথে যায়।

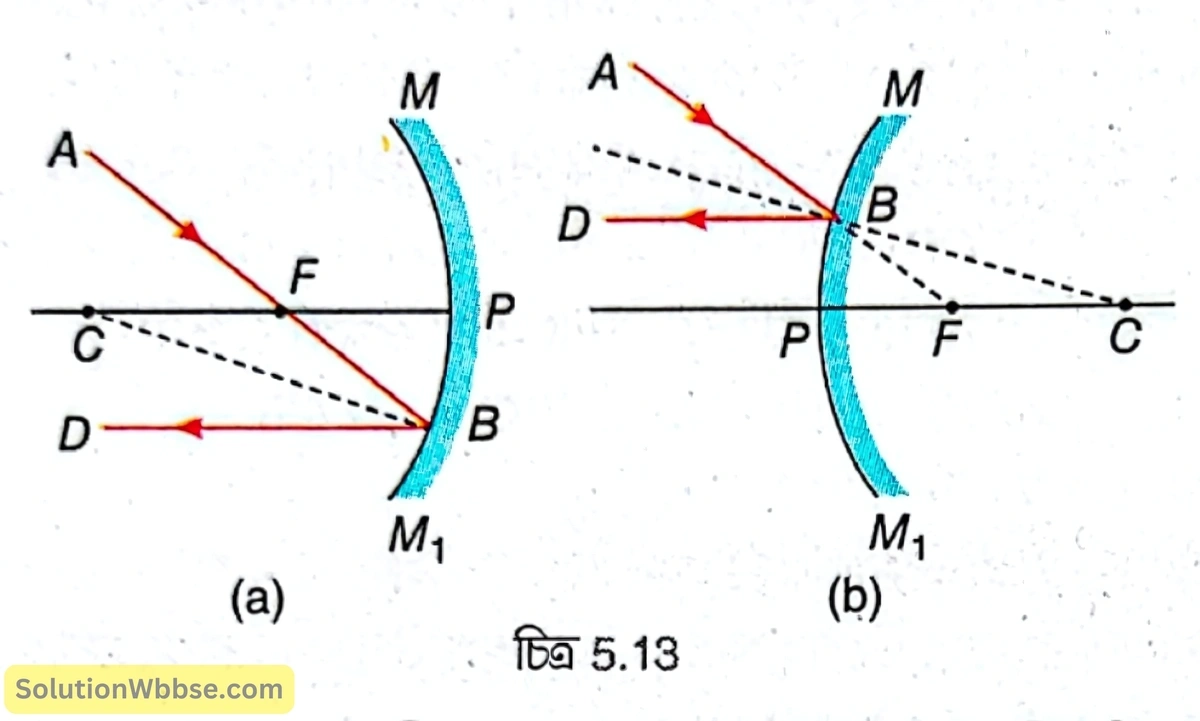
মুখ্য ফোকাসগামী বা মুখ্য ফোকাসের দিকে পরিচালিত রশ্মি – অবতল দর্পণের মুখ্য ফোকাসগামী (F) কোনো রশ্মি AB [চিত্র 5.13 (a)] দর্পণ দ্বারা প্রতিফলনের পর প্রধান অক্ষের সমান্তরালভাবে BD পথে যায় আবার উত্তল দর্পণের মুখ্য ফোকাসের (F) দিকে পরিচালিত কোনো রশ্মি AB [চিত্র 5.13 (b)], দর্পণ দ্বারা প্রতিফলনের পর প্রধান অক্ষের সমান্তরালভাবে BD পথে যায়।

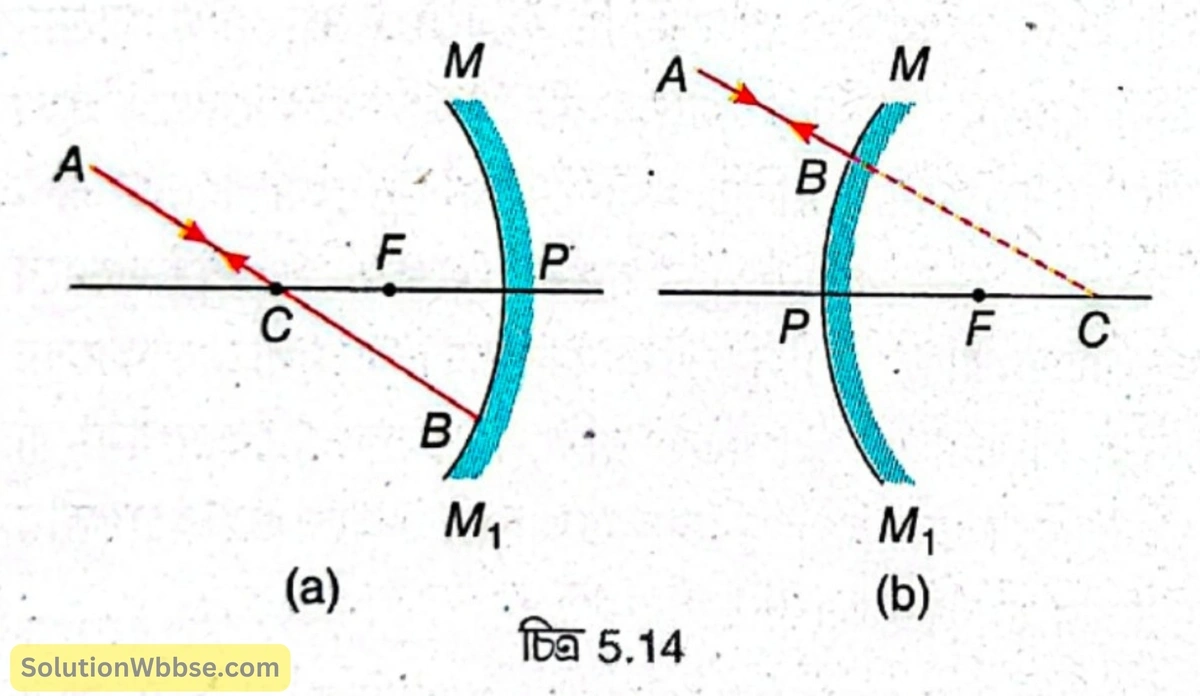
বক্রতা কেন্দ্রগামী বা বক্রতা কেন্দ্রের দিকে পরিচালিত রশ্মি – অবতল দর্পণের বক্রতা কেন্দ্রগামী [চিত্র 5.14 (a)] ও উত্তল দর্পণের বক্রতা কেন্দ্রের দিকে পরিচালিত [চিত্র 5.14 (b)] রশ্মি AB দর্পণের ওপর লম্বভাবে আপতিত হওয়ায় আপতন কোণের মান হয় 0°, তাই প্রতিফলন কোণও 0° হয়। ফলে প্রতিফলিত রশ্মি (BA) একই পথে ফিরে যায়।

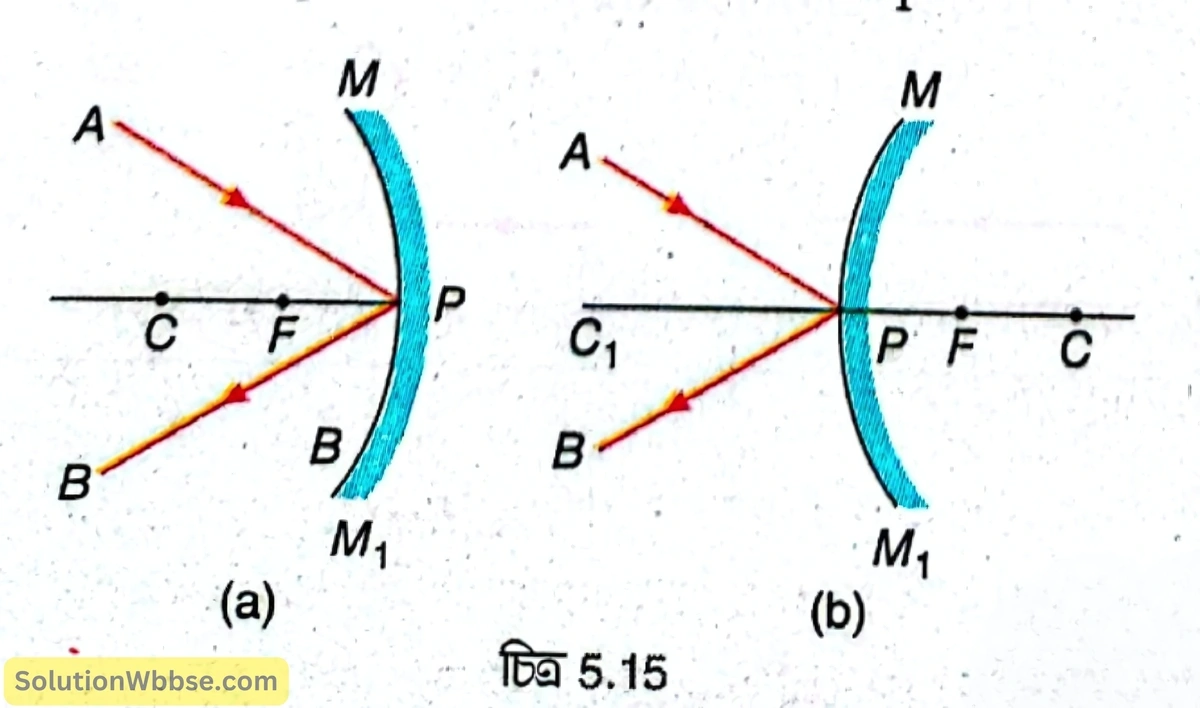
গোলীয় দর্পণের মেরুতে আপতিত রশ্মি – গোলীয় দর্পণের মেরুতে (P) AP রশ্মি আপতিত হয়ে PB পথে প্রতিফলিত হয়। এখানে অভিলম্ব হল প্রধান অক্ষ। অবতল দর্পণের ক্ষেত্রে [চিত্র 5.15 (a)] আপতন কোণ \(\angle APC\;= \) প্রতিফলন কোণ \(\angle BPC \) ও উত্তল দর্পণের ক্ষেত্রে [চিত্র 5.15 (b)] আপতন কোণ \( \angle APC_1\) = প্রতিফলন কোণ \(\angle BPC_1 \)।

গোলীয় দর্পণে অভিসারী রশ্মিগুচ্ছের প্রতিফলন চিত্রের সাহায্যে দেখাও।

5.16 (a) নং চিত্রে একটি অবতল দর্পণের ওপর অভিসারী রশ্মিগুচ্ছ আপতিত হয়েছে। দর্পণটি না থাকলে অভিসারী রশ্মিগুচ্ছ দর্পণের পিছনে \( O \) বিন্দুতে মিলিত হত। দর্পণ দ্বারা প্রতিফলনের পর প্রতিফলিত রশ্মিগুচ্ছ প্রধান অক্ষের ওপর \( I \) বিন্দুতে মিলিত হয়। এখানে \( O \) হল অসৎ বস্তু ও \( I \) হল তার সদবিম্ব এবং অভিসারী রশ্মিগুচ্ছ প্রতিফলনের পরও অভিসারী থাকে।

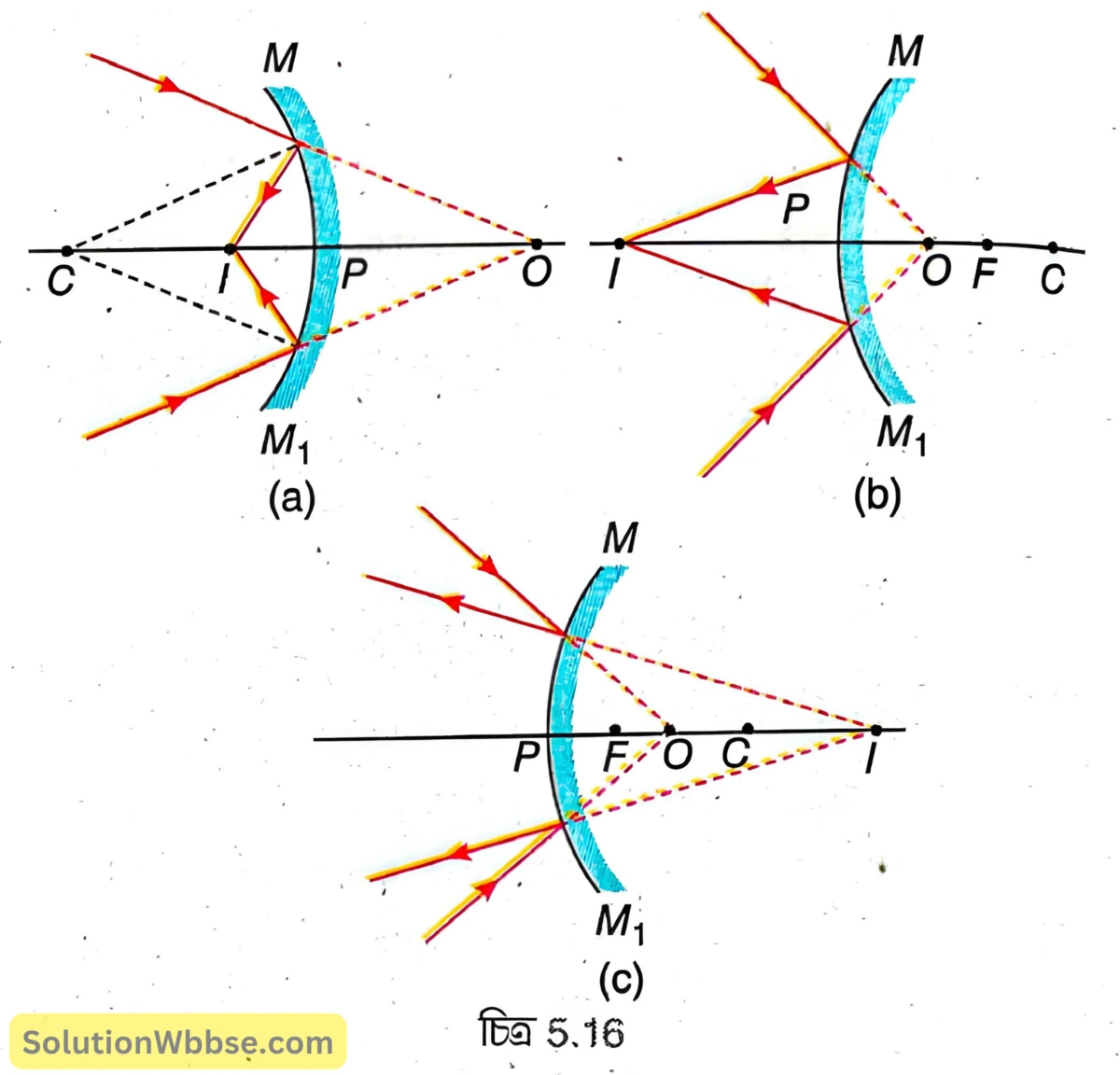
আবার উত্তল দর্পণে অভিসারী রশ্মিগুচ্ছ আপতিত হলে কী হবে তা নির্ভর করে দর্পণের অনুপস্থিতিতে রশ্মিগুচ্ছ দর্পণের পিছনে কোথায় মিলিত হবে তার ওপর। যদি দর্পণের অনুপস্থিতিতে অভিসারী রশ্মিগুচ্ছ ফোকাস দূরত্বের চেয়ে কম দূরত্বে মিলিত হয় [চিত্র 5.16 (b)] তাহলে দর্পণ দ্বারা প্রতিফলনের পর প্রতিফলিত রশ্মিগুচ্ছ প্রধান অক্ষের ওপর \( I \) বিন্দুতে মিলিত হয়, অর্থাৎ \( O \) অসৎ বস্তুর সদবিম্ব গঠিত হয় বা অভিসারী রশ্মিগুচ্ছ প্রতিফলনের পরও অভিসারী থাকে। আবার যদি দর্পণের অনুপস্থিতিতে অভিসারী রশ্মিগুচ্ছ ফোকাস দূরত্বের চেয়ে বেশি দূরত্বে মিলিত হয় [চিত্র 5.16 (c)] তাহলে দর্পণ দ্বারা প্রতিফলনের পর প্রতিফলিত রশ্মিগুচ্ছ প্রধান অক্ষের ওপর \( I \) বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়, অর্থাৎ \( O \) অসৎ বস্তুর অসদবিম্ব গঠিত হয় বা অভিসারী রশ্মিগুচ্ছ প্রতিফলনের পর অপসারী হয়।

গোলীয় দর্পণে অপসারী রশ্মিগুচ্ছের প্রতিফলন চিত্রের সাহায্যে দেখাও।

5.17 (a) নং চিত্রে একটি অবতল দর্পণের প্রধান অক্ষের ওপর একটি বিন্দুবস্তু \( O \) থেকে আগত অপসারী রশ্মিগুচ্ছ দর্পণ দ্বারা প্রতিফলনের পর দর্পণের সামনে প্রধান অক্ষের ওপর \( I \) বিন্দুতে মিলিত হয় অর্থাৎ এখানে অপসারী রশ্মিগুচ্ছ প্রতিফলনের পর অভিসারী রশ্মিগুচ্ছে পরিণত হয়। তবে অবতল দর্পণে আপতিত অপসারী রশ্মিগুচ্ছ প্রতিফলনের পর অভিসারী, সমান্তরাল না অপসারী রশ্মিগুচ্ছে পরিণত হবে তা নির্ভর করে বিন্দুবস্তুর অবস্থানের ওপর। বিন্দুবস্তু, ফোকাসের বেশি দূরত্বে থাকলে প্রতিফলিত রশ্মিগুচ্ছ হবে অভিসারী, বিন্দুবস্তু ফোকাসে থাকলে প্রতিফলিত রশ্মিগুচ্ছ হবে সমান্তরাল এবং ফোকাসের কম দূরত্বে থাকলে প্রতিফলিত রশ্মিগুচ্ছ হবে অপসারী।

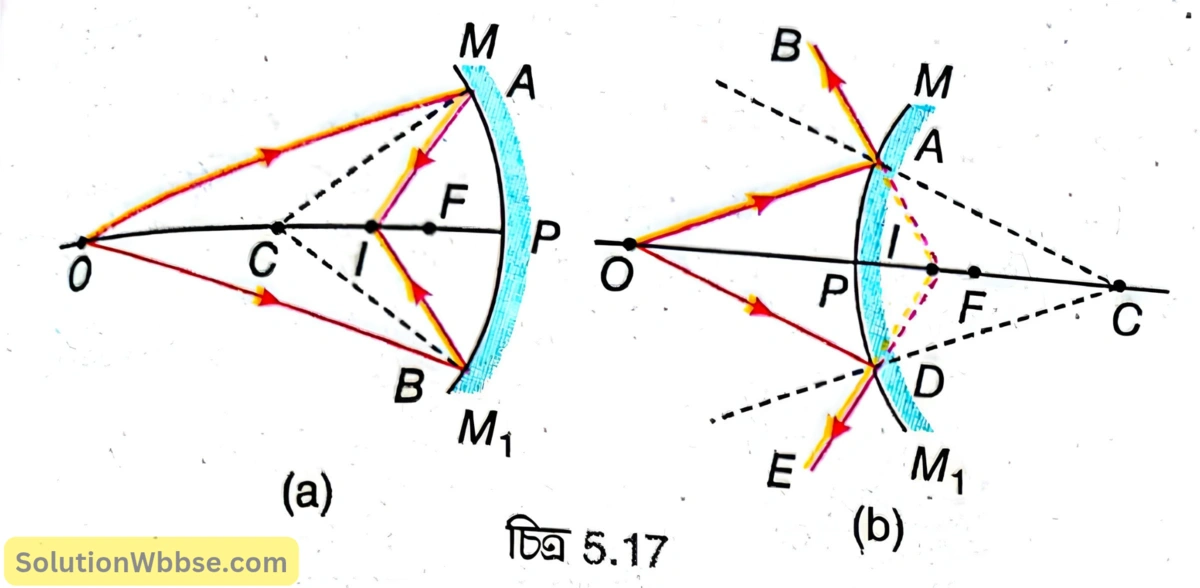
আবার 5.17 (b) নং চিত্রে উত্তল দর্পণের প্রধান অক্ষের ওপর অবস্থিত একটি বিন্দুবস্তু \( O \) থেকে আগত অপসারী আলোক রশ্মিগুচ্ছ দর্পণ দ্বারা প্রতিফলনের পর আরও অপসারী হয় এবং দর্পণের পিছনে \( I \) বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়।

অবতল দর্পণ দ্বারা একটি বিস্তৃত বস্তুর বিবর্ধিত সদবিম্ব গঠন চিত্রসহ ব্যাখ্যা করো।

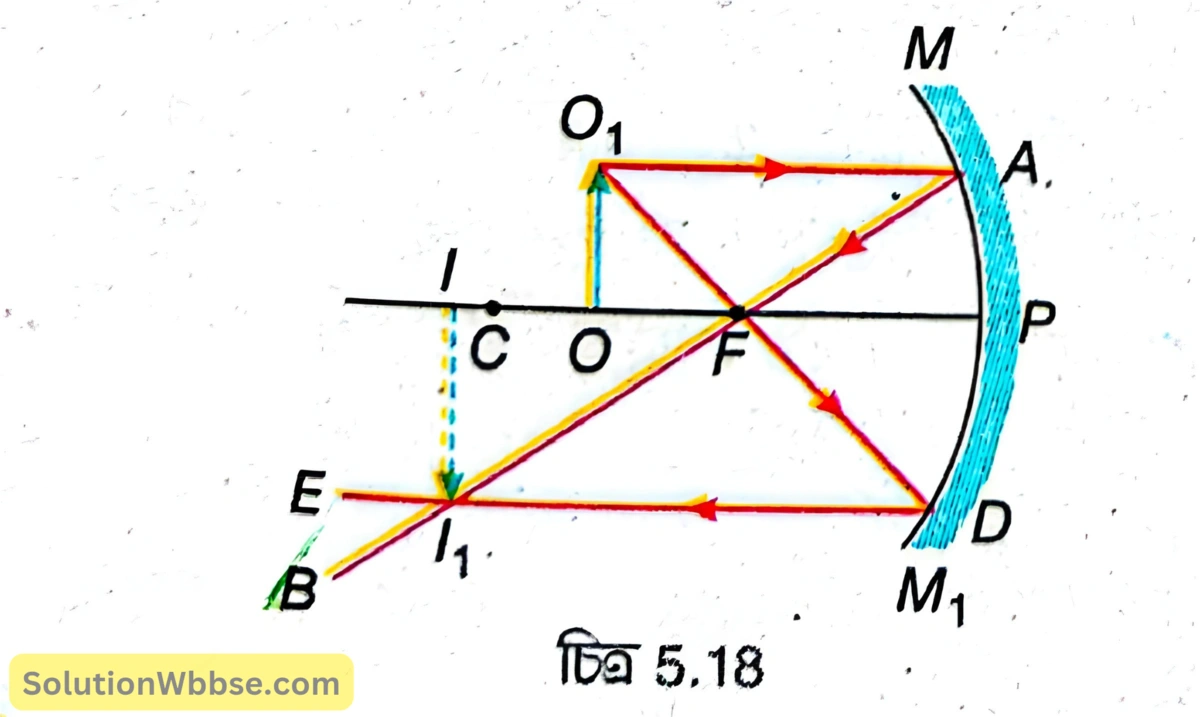
ক্ষুদ্র উন্মেষযুক্ত একটি অবতল দর্পণের \( MPM_1 \) হল প্রধান ছেদ [চিত্র 5.18]। \( P,F \) ও \( C \) হল যথাক্রমে অবতল দর্পণটির মেরু, মুখ্য ফোকাস ও বক্রতা কেন্দ্র। অবতল দর্পণের ফোকাস ও বক্রতা কেন্দ্রের মাঝে প্রধান অক্ষের ওপর লম্বভাবে অবস্থিত \( OO_1 \) হল একটি বিস্তৃত বস্তু। \( O_1 \) থেকে প্রধান অক্ষের সমান্তরাল \( O_1A \) রশ্মি দর্পণ দ্বারা প্রতিফলনের পর মুখ্য ফোকাস \( F \) -এর মধ্য দিয়ে \( AB \) পথে যায়। মুখ্য ফোকাসগামী অপর একটি রশ্মি \( O_1D \) দর্পণ দ্বারা প্রতিফলনের পর প্রধান অক্ষের সমান্তরালভাবে \( DE \) পথে যায়। প্রতিফলিত রশ্মি দুটি \( I_1 \) বিন্দুতে মিলিত হয়। \( I_1 \) থেকে প্রধান অক্ষের ওপর \( I_1I \) লম্ব টানা হল। \( II_1 \) হল \( OO_1 \) বস্তুর সদবিম্ব। এখানে প্রতিবিম্বের সাইজ বস্তুর চেয়ে বড়ো তাই প্রতিবিম্ব বিবর্ধিত এবং প্রতিবিম্ব বস্তু সাপেক্ষে উলটো তাই প্রতিবিম্ব অবশীর্ষ, অর্থাৎ এখানে প্রতিবিম্ব সৎ, বিবর্ধিত ও অবশীর্ষ।

অবতল দর্পণ দ্বারা একটি বিস্তৃত বস্তুর বিবর্ধিত অসদবিম্ব গঠন চিত্রসহ ব্যাখ্যা করো।

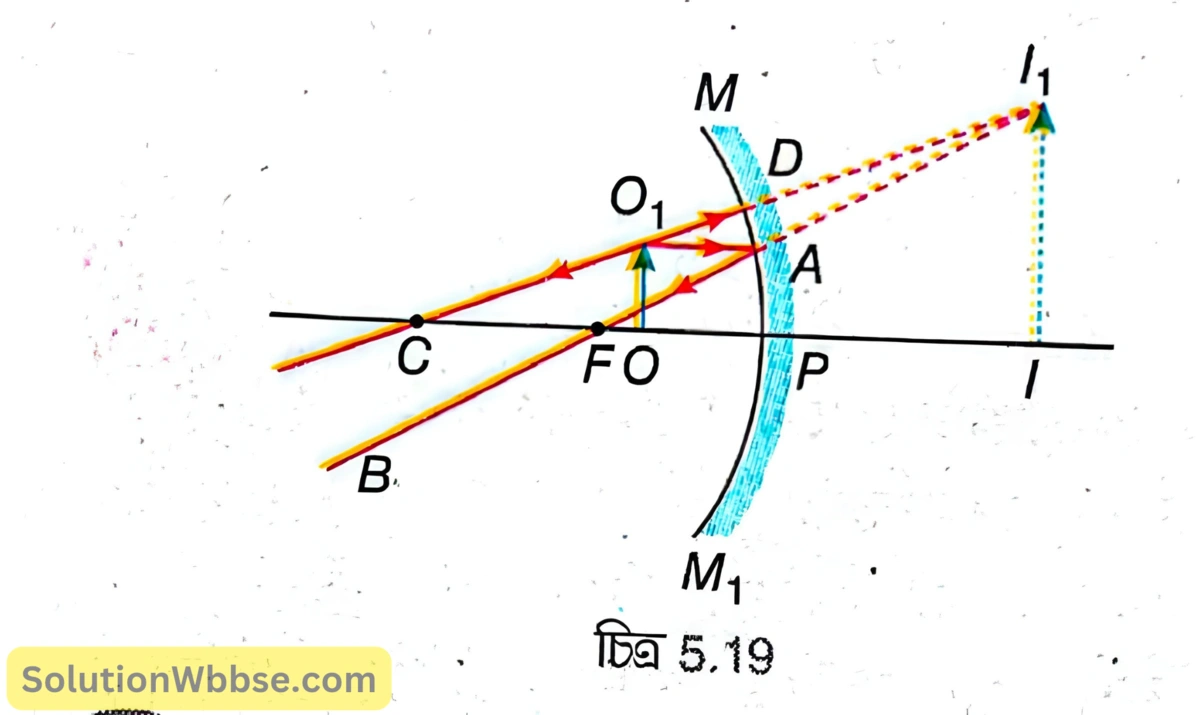
ক্ষুদ্র উন্মেষযুক্ত একটি অবতল দর্পণের \( MPM_1 \) হল প্রধান ছেদ [চিত্র 5.19]। \( P,F \) ও \( C \) হল যথাক্রমে অবতল দর্পণটির মেরু, মুখ্য ফোকাস ও বক্রতা কেন্দ্র। অবতল দর্পণের ফোকাসের চেয়ে কম দূরত্বে প্রধান অক্ষের ওপর লম্বভাবে অবস্থিত \( OO_1 \) হল একটি বিস্তৃত বস্তু। \( O_1 \) থেকে প্রধান অক্ষের সমান্তরাল \( O_1A \) রশ্মি দর্পণ দ্বারা প্রতিফলনের পর মুখ্য ফোকাস \( F \) -এর মধ্য দিয়ে যায়। অপর একটি রশ্মি \( O_1D \) লম্বভাবে আপতিত হয়ে বক্রতা কেন্দ্র \( C \) -এর মধ্য দিয়ে \( DC \) পথে প্রতিফলিত হয়। প্রতিফলিত রশ্মি দুটি অপসারী হওয়ায় প্রতিফলনের পর মিলিত হয় না। রশ্মি দুটিকে পিছন দিকে বাড়ালে \( I_1 \) বিন্দুতে মিলিত হয় অর্থাৎ প্রতিফলিত রশ্মি দুটি \( I_1 \) থেকে অপসৃত হচ্ছে বলে মনে হয়। \( I_1 \) থেকে প্রধান অক্ষের ওপর \( I_1I \) লম্ব টানা হল। \( II_1 \) হল \( OO_1 \) বস্তুর অসদবিম্ব। এখানে প্রতিবিম্বের সাইজ বস্তুর চেয়ে বড়ো তাই প্রতিবিম্ব বিবর্ধিত এবং প্রতিবিম্ব বস্তু সাপেক্ষে সোজা তাই প্রতিবিম্ব সমশীর্ষ, অর্থাৎ এখানে প্রতিবিম্ব অসৎ, বিবর্ধিত ও সমশীর্ষ।

অবতল দর্পণ দ্বারা একটি বিন্দুবস্তুর সদবিম্ব গঠন চিত্রসহ ব্যাখ্যা করো।

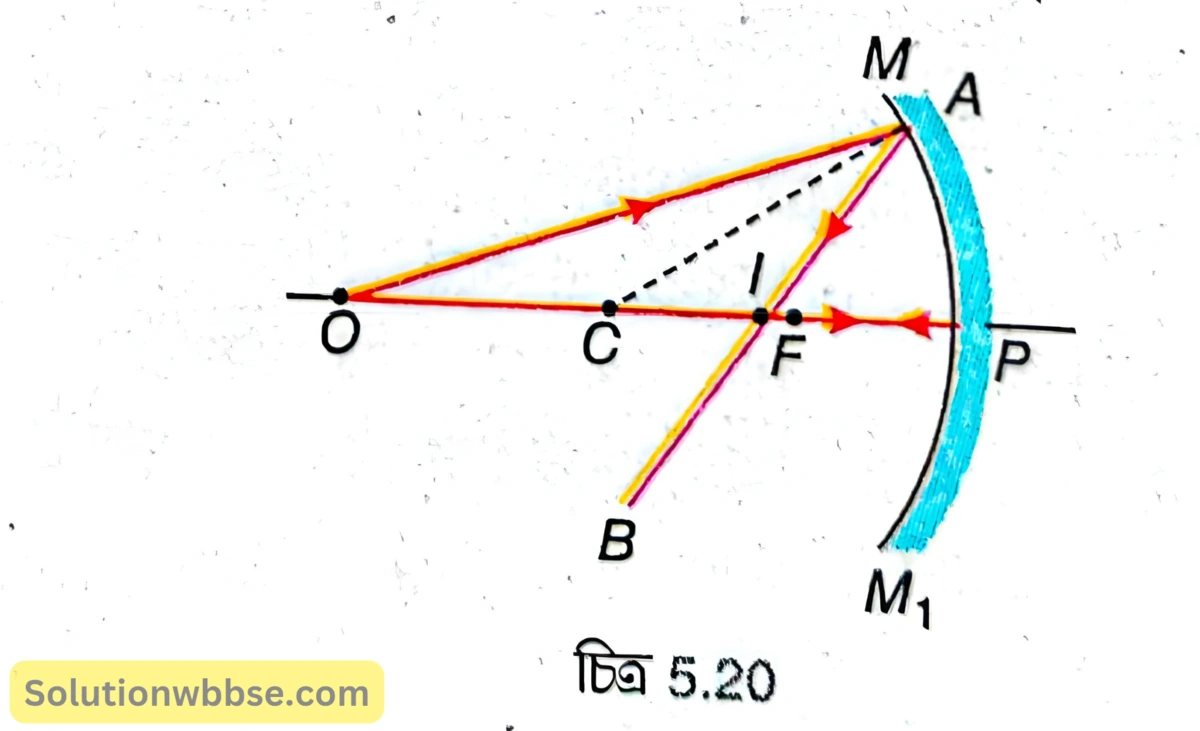
ক্ষুদ্র উন্মেষযুক্ত একটি অবতল দর্পণের \( MPM_1 \) হল প্রধান ছেদ [চিত্র 5.20]। \( P,F \) ও \( C \) হল যথাক্রমে অবতল দর্পণটির মেরু, মুখ্য ফোকাস ও বক্রতা কেন্দ্র। অবতল দর্পণের প্রধান অক্ষের ওপর ফোকাস থেকে বেশি দূরত্বে \( O \) একটি বিন্দুবস্তু। \( O \) থেকে আগত \( OA \) রশ্মি দর্পণ দ্বারা প্রতিফলনের পর \( AB \) পথে প্রতিফলিত হয়, এখানে \( AC \) হল \( A \) বিন্দুতে দর্পণের ওপর অভিলম্ব এবং \( \angle OAC=\angle CAB \) । \( O \) থেকে প্রধান অক্ষ বরাবর আগত রশ্মি লম্বভাবে \( P \) বিন্দুতে আপতিত হয়ে \( PC \) বরাবর প্রতিফলিত হয়। প্রতিফলিত রশ্মিদুটি প্রধান অক্ষের ওপর \( I \) বিন্দুতে মিলিত হয়। \( I \) হল \( O \) বিন্দুবস্তুর সদবিম্ব।

অবতল দর্পণ দ্বারা একটি বিন্দুবস্তুর অসদবিম্ব গঠন চিত্রসহ ব্যাখ্যা করো।

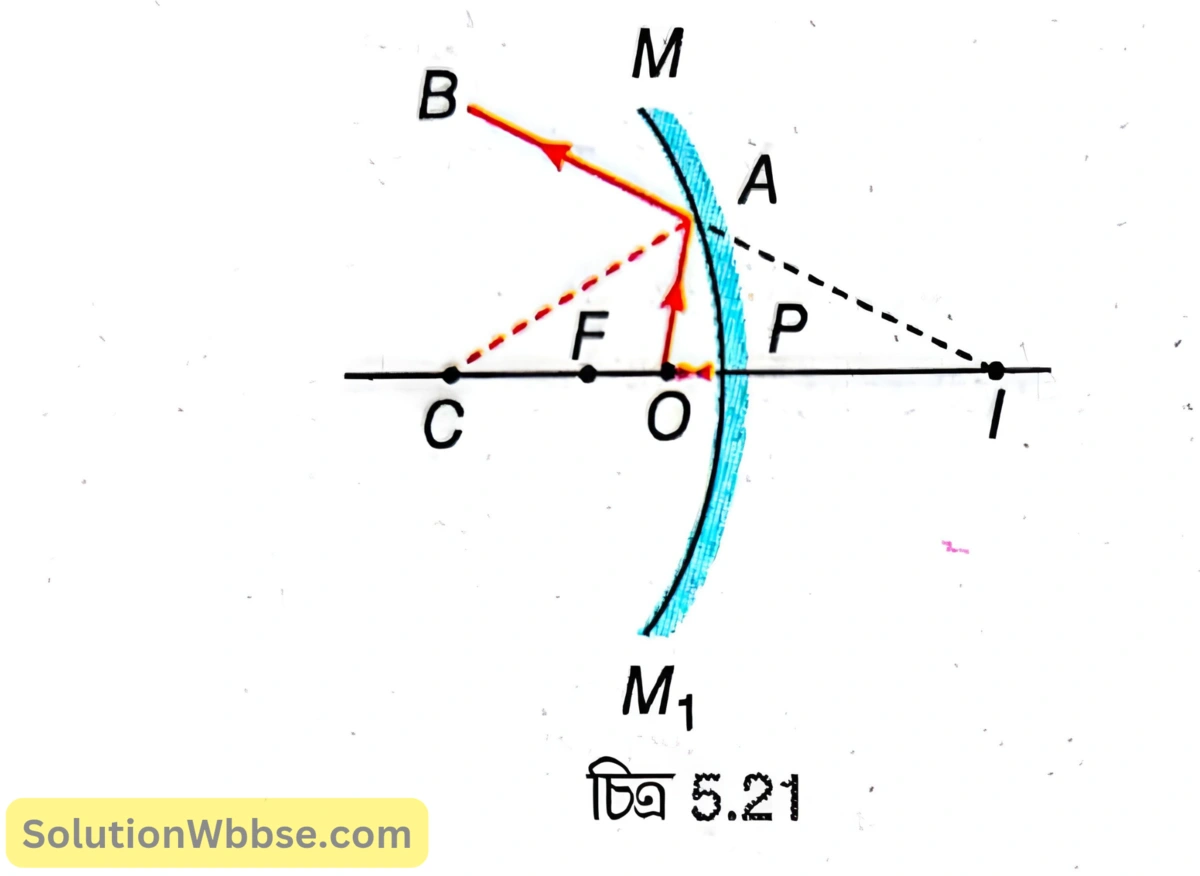
ক্ষুদ্র উন্মেষযুক্ত একটি অবতল দর্পণের \( MPM_1 \) হল প্রধান ছেদ [চিত্র 5.21]। \( P,F \) ও \( C \) হল যথাক্রমে অবতল দর্পণটির মেরু, মুখ্য ফোকাস ও বক্রতা কেন্দ্র। অবতল দর্পণের প্রধান অক্ষের ওপর মেরু ও ফোকাসের মাঝে \( O \) একটি বিন্দুবস্তু। \( O \) থেকে আগত \( OA \) রশ্মি দর্পণ দ্বারা প্রতিফলনের পর \( AB \) পথে প্রতিফলিত হয়। এখানে \( AC \) হল \( A \) বিন্দুতে দর্পণের ওপর অভিলম্ব এবং \( \angle OAC=\angle CAB \) । \( O \) থেকে প্রধান অক্ষ বরাবর আগত রশ্মি লম্বভাবে \( P \) বিন্দুতে আপতিত হয়ে \( PC \) বরাবর প্রতিফলিত হয়। প্রতিফলিত রশ্মি দুটি অপসারী হওয়ায় প্রতিফলনের পর মিলিত হয় না। রশ্মি দুটিকে পিছন দিকে বাড়ালে \( I \) বিন্দুতে মিলিত হয়। \( I \) হল \( O \) বিন্দুবস্তুর অসদবিম্ব।

গোলীয় দর্পণের ব্যবহার কী?

গোলীয় দর্পণের ব্যবহার –

অবতল দর্পণ –

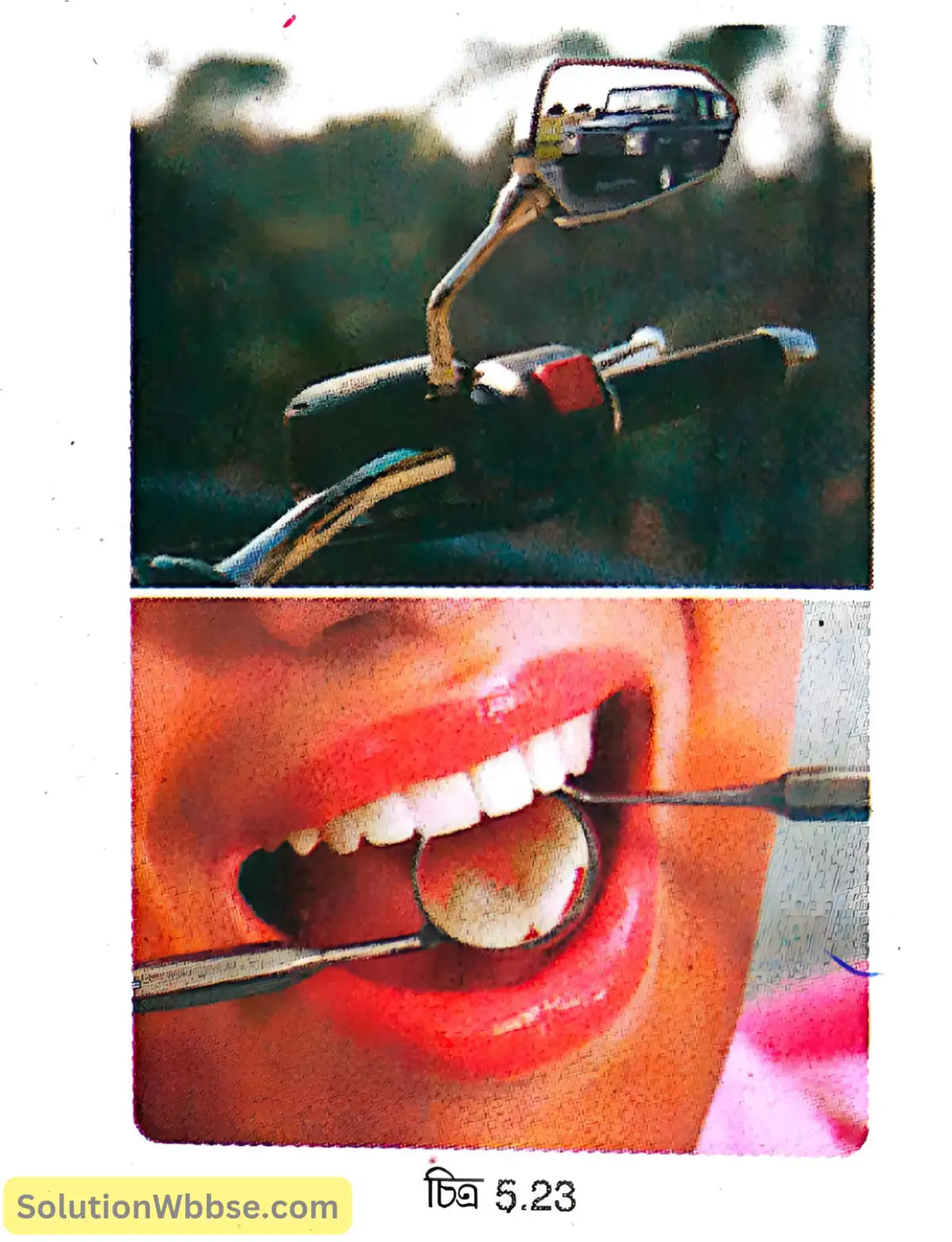
• টর্চ, সার্চলাইট বা গাড়ির হেডলাইটে পালিশ করা ধাতব অবতল তল ব্যবহার করা হয় যা অবতল দর্পণ হিসেবে কাজ করে। এইসব লাইটের বাতি দর্পণের ফোকাসে রাখা হয় ফলে বাতি থেকে নির্গত আলোকরশ্মি অবতল প্রতিফলকে প্রতিফলিত হয়ে সমান্তরাল রশ্মিগুচ্ছে পরিণত হয়। এইজন্য অনেক দূর পর্যন্ত দেখা যায় এবং গাড়ির চালকের খুব সুবিধা হয়। এই সুবিধার জন্য দন্ত চিকিৎসক, ENT বিশেষজ্ঞরা মাথার দর্পণ (head mirror) হিসেবে অবতল দর্পণ ব্যবহার করেন, যাতে সমান্তরাল রশ্মিগুচ্ছকে কোনো নির্দিষ্ট জায়গায় ফোকাস করা যায়। এর ফলে দাঁত, কান বা নাকের ভিতর কোনো জায়গা পরীক্ষা করতে ডাক্তারদের সুবিধা হয়।
• অবতল দর্পণের ফোকাসের মধ্যে কোনো বস্তু থাকলে তার বিবর্ধিত অসদবিম্ব গঠিত হয়, এই ধর্মকে কাজে লাগিয়ে দাড়ি কামানোর কাজে বা বিউটি পার্লারে অবতল দর্পণ ব্যবহৃত হয়।

উত্তল দর্পণ –

• মোটর সাইকেল, বাস, লরি ইত্যাদি গাড়িতে ভিউফাইন্ডার হিসেবে উত্তল দর্পণ ব্যবহৃত হয়। উত্তল দর্পণ তার সামনে থাকা কোনো বস্তুর সর্বদা খর্বকায় অসদবিম্ব গঠন করে। ফলে কোনো গাড়ির চালক তাঁর পিছনে অনেক দূরের কোনো গাড়ি বা বস্তু বা ব্যক্তির খর্বকায় অসদবিম্ব উত্তল দর্পণে দেখতে পান এবং দুর্ঘটনা না ঘটিয়ে গাড়ি চালাতে সুবিধা হয়।
• স্ট্রিট ল্যাম্পের প্রতিফলক হিসেবে উত্তল দর্পণ ব্যবহৃত হয়। এই দর্পণ, স্ট্রিট ল্যাম্পের আলোকে অনেকটা এলাকা জুড়ে ছড়িয়ে দেয়।

অধিবৃত্তাকার দর্পণ কোন কোন যন্ত্রে ব্যবহার করা হয়?

বর্তমানে বেশিরভাগক্ষেত্রে মোটরগাড়ির হেডলাইট এবং সার্চলাইটে গোলীয় দর্পণ ব্যবহার না করে অধিবৃত্তাকার দর্পণ ব্যবহার করা হয়। কারণ এক্ষেত্রে বেশি প্রস্থচ্ছেদযুক্ত সমান্তরাল রশ্মির প্রয়োজন হয়, যাতে বেশ কিছুটা অঞ্চল যেন ভালোভাবে আলোকিত হয়।

তোমাকে তিনটি দর্পণ দেওয়া হল – একটি সমতল, একটি উত্তল ও একটি অবতল। স্পর্শ না করে কীভাবে দর্পণগুলিকে শনাক্ত করবে?

সমতল দর্পণ কোনো বস্তুর সমান সাইজের অসদবিম্ব গঠন করে। উত্তল দর্পণ সর্বদা কোনো বস্তুর খর্বকায় অসদবিম্ব গঠন করে এবং অবতল দর্পণের ফোকাস দূরত্বের কম দূরত্বে একটি বস্তু রাখলে বস্তুটির বিবর্ধিত অসদবিম্ব গঠিত হয়।

একটি পেনসিলকে কোনো দর্পণের খুব কাছে ধরলে যদি সমান সাইজের অসদবিম্ব গঠিত হয় তাহলে দর্পণটি সমতল, যদি খর্বকায় অসদবিম্ব গঠিত হয়, তাহলে দর্পণটি উত্তল এবং যদি বিবর্ধিত অসদবিম্ব গঠিত হয়, তাহলে দর্পণটি অবতল।

গোলীয় দর্পণের অনুবন্ধী ফোকাস যুগল কাকে বলে?

গোলীয় দর্পণের অনুবন্ধী ফোকাস যুগল হল এমন দুটি বিন্দু, যার একটিতে বস্তু রাখলে অন্যটিতে প্রতিবিম্ব গঠিত হয়। অসদবিম্ব গঠিত হয় দর্পণের পিছনে; তাই অসদবিম্বের ক্ষেত্রে অনুবন্ধী ফোকাস যুগল দর্পণের দুই বিপরীত দিকে থাকে। অন্যদিকে, সদবিম্ব গঠিত হয় দর্পণের সামনে (শুধুমাত্র অবতল দর্পণের ক্ষেত্রে); তাই এক্ষেত্রে অনুবন্ধী ফোকাস যুগল থাকে দর্পণের একই পাশে।

কোনো গোলীয় দর্পণকে জলে নিমজ্জিত করলে ফোকাস দৈর্ঘ্যের কীরূপ পরিবর্তন হবে?

গোলীয় দর্পণে আলোর প্রতিফলন হয় এবং আলোর প্রতিফলন সংক্রান্ত সূত্রগুলি মাধ্যমের প্রকৃতির ওপর নির্ভর করে না, তাই কোনো গোলীয় দর্পণকে জলে নিমজ্জিত করলে ফোকাস দৈর্ঘ্য অপরিবর্তিত থাকবে।

আলোর প্রতিসরণ ও প্রিজম

আলোর প্রতিসরণ কাকে বলে?

আলোকরশ্মি কোনো স্বচ্ছ ও সমসত্ত্ব মাধ্যমের মধ্য দিয়ে যেতে যেতে অন্য কোনো স্বচ্ছ ও সমসত্ত্ব মাধ্যমের বিভেদতলে তির্যকভাবে আপতিত হলে, দুই মাধ্যমের বিভেদতলে আলোকরশ্মির গতির অভিমুখের পরিবর্তন হয়, এই ঘটনাকে আলোর প্রতিসরণ বলা হয়।

আলোক সাপেক্ষে লঘু ও ঘন মাধ্যম বলতে কী বোঝ?

দুটি আলোকীয় মাধ্যমের মধ্যে যেটিতে আলোর গতিবেগ বেশি সেটিকে লঘুতর মাধ্যম এবং যেটিতে আলোর গতিবেগ কম সেটিকে ঘনতর মাধ্যম বলা হয়। যেমন জল ও কাচে আলোর বেগ যথাক্রমে \( 2.25\times10^8m/s \) ও \( 2\times10^8m/s, \) তাই আলোক সাপেক্ষে জল হল লঘুতর মাধ্যম এবং কাচ হল ঘনতর মাধ্যম।

আলোকরশ্মি (i) লঘু থেকে ঘন (ii) ঘন থেকে লঘু মাধ্যমে প্রবেশ করলে অভিমুখের কীরূপ পরিবর্তন হয় তা রশ্মিচিত্রের সাহায্যে দেখাও।

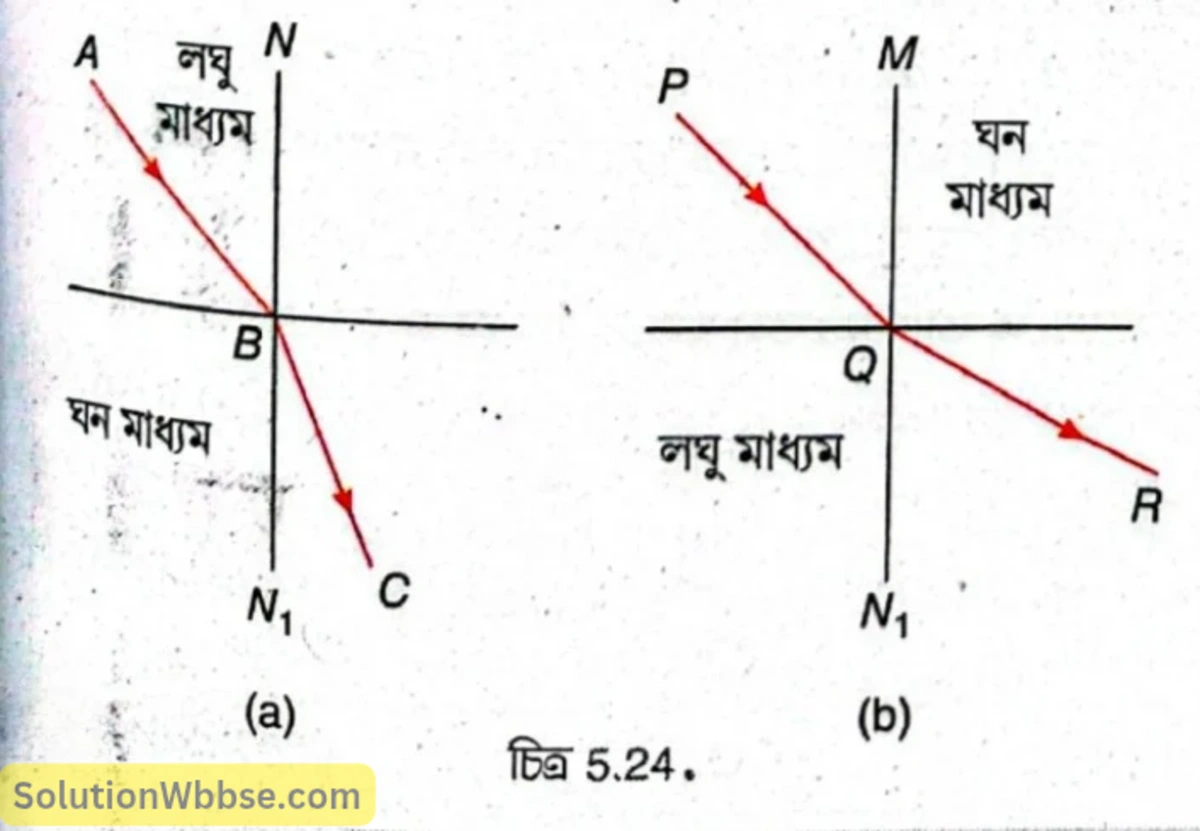
1. আলোকরশ্মি লঘু মাধ্যম থেকে ঘন মাধ্যমে প্রবেশ করলে প্রতিসৃত রশ্মি অভিলম্বের দিকে বেঁকে যায় [চিত্র 5.24 (a)]
2. আলোকরশ্মি ঘন মাধ্যম থেকে লঘু মাধ্যমে প্রবেশ করলে প্রতিসৃত রশ্মি অভিলম্ব থেকে দূরে সরে যায় [চিত্র 5.24 (b)]

আলোর প্রতিসরণে চ্যুতিকোণ নির্ণয় করো।

5.25 (a) ও (b) নং চিত্রে যথাক্রমে আলোকরশ্মির লঘু মাধ্যম থেকে ঘন মাধ্যমে ও ঘন মাধ্যম থেকে লঘু মাধ্যমে প্রতিসরণ দেখানো হয়েছে যেখানে AO আপতিত রশ্মি, OB প্রতিসূত রশ্মি, XY দুই মাধ্যমের বিভেদতল, MN হল আপতন বিন্দুতে কোণ \( \left(\angle AOM\right)i \) ও প্রতিসরণ কোণ \( \left(\angle BON\right)r \)। দুই মাধ্যমের বিভেদতলে যদি আলোকরশ্মির অভিমুখ পরিবর্তিত না হত তাহলে আলোকরশ্মি OC পথে যেত; তাই ∠BOC = δ হল প্রতিসরণে চ্যুতিকোণ।

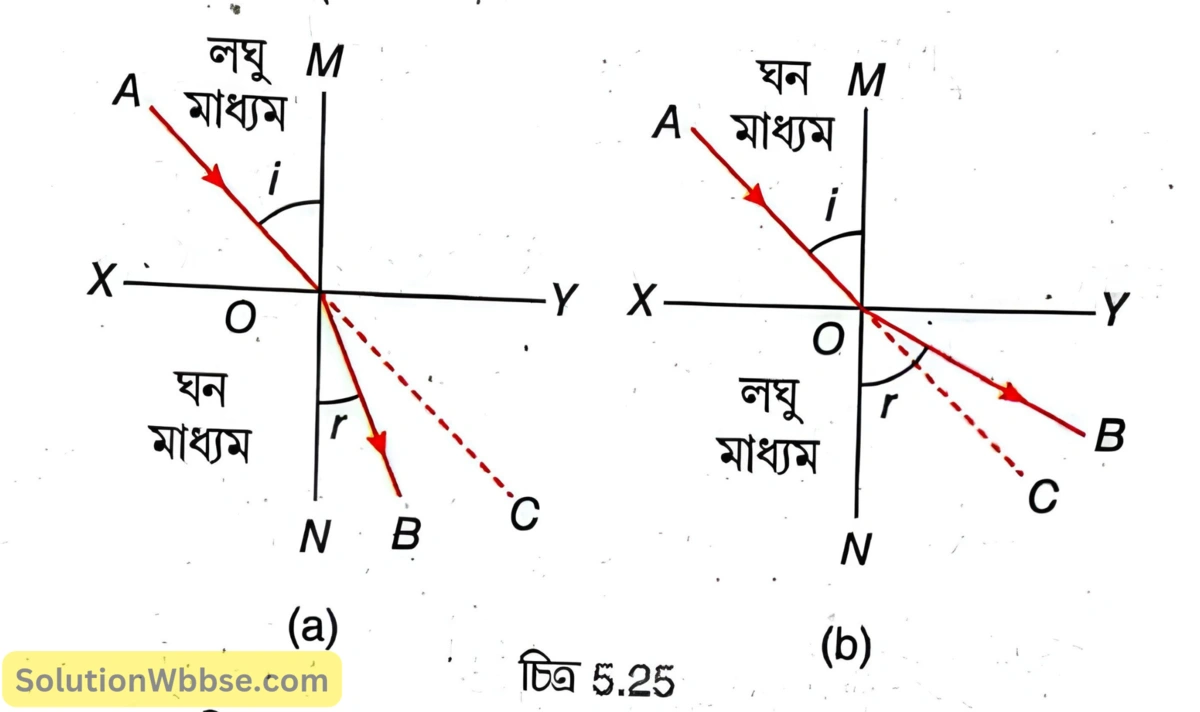
আলোকরশ্মির লঘু থেকে ঘন মাধ্যমে প্রতিসরণে [চিত্র 5.25 (a)] \( r < i \) হয়।

5.25 (a) নং চিত্র থেকে পাই,
\( \angle NOC = \angle AOM \) [বিপ্রতীপ কোণ]
বা, \( \angle BON + \angle BOC = \angle AOM \)
বা, \( \angle BOC = \angle AOM – \angle BON \)
∴ \( \delta = i – r \) ……….. (1)

আবার, আলোকরশ্মির ঘন থেকে লঘু মাধ্যমে প্রতিসরণে [চিত্র 5.25 (b)] \( r > i \) হয়।

5.25 (b) নং চিত্র থেকে পাই,
\( \angle NOC = \angle AOM \) [বিপ্রতীপ কোণ]
বা, \( \angle BON – \angle BOC = \angle AOM \)
বা, \( \angle BOC = \angle BON – \angle AOM \)
বা, \( \delta = r – i \)

আলোর প্রতিসরণের সূত্র দুটি লেখো।

আলোর প্রতিসরণের সূত্র দুটি হল –

1. আপতিত রশ্মি, প্রতিসৃত রশ্মি ও আপতন বিন্দুতে দুই মাধ্যমের বিভেদতলের ওপর অঙ্কিত অভিলম্ব একই সমতলে থাকে।
2. দুটি নির্দিষ্ট মাধ্যম ও নির্দিষ্ট বর্ণের আলোকরশ্মির প্রতিসরণের ক্ষেত্রে আপতন কোণের sine এবং প্রতিসরণ কোণের sine –এর অনুপাত ধ্রুবক হয়।

একটি সহজ পরীক্ষার সাহায্যে প্রতিসরণের সূত্র দুটি বোঝাও।

একটি আয়তাকার কাচের স্ল্যাব নিয়ে সাদা কাগজে স্ল্যাবটি রেখে পেনসিল দিয়ে দাগ দেওয়া হল। 5.26 নং চিত্রে \( PQRS \) হল স্ল্যাবের অবস্থান। এবার চারটি পিন নিয়ে \( PQ \) –এর ওপরের দিকে দুটি পিন \( P_1,P_2 \) –কে এমনভাবে বসানো হল যাতে \( P_1 \) ও \( P_2 \) –এর সংযোজী সরলরেখা \( PQ \) –এর সঙ্গে তির্যকভাবে থাকে। এবার \( SR \) প্রান্ত থেকে দেখলে \( P_1 \) ও \( P_2 \) –এর প্রতিবিম্ব দেখা যাবে। বাকি দুটি পিন \( P_3 \) ও \( P_4 \) -কে এমনভাবে বসানো হল যাতে \( P_1 \) ও \( P_2 \) পিন দুটির প্রতিবিম্ব এবং \( P_3 \) ও \( P_4 \) একই সরলরেখায় থাকে। এবার স্ল্যাব ও পিনগুলিকে তুলে পিনগুলির পাদবিন্দু পেনসিল দিয়ে বৃত্তাকারে দাগ দেওয়া হল। \( P_1,P_2 \) এবং \( P_3,P_4 \) যুক্ত করে বর্ধিত করা হল যাতে বর্ধিত রেখা দুটি \( PQ \) ও \( SR \) –কে যথাক্রমে \( B \) ও \( C \) বিন্দুতে ছেদ করে। \( B,C \) যুক্ত করা হল। এরপর \( B \) বিন্দুতে \( PQ \) –এর ওপর \( N_1N_2 \) লম্ব টানা হল। এখানে \( AB \) হল আপতিত রশ্মি, \( BC \) হল কাচ মাধ্যমে প্রতিসৃত রশ্মি এবং \( N_1N_2 \) হল \( B \) বিন্দুতে দুই মাধ্যমের বিভেদতলের ওপর অঙ্কিত অভিলম্ব। এই পরীক্ষা থেকে দেখা গেল, \( AB,BC \) ও \( N_1N_2 \) একই সমতলে আছে। এটিই প্রতিসরণের প্রথম সূত্রের বক্তব্য।

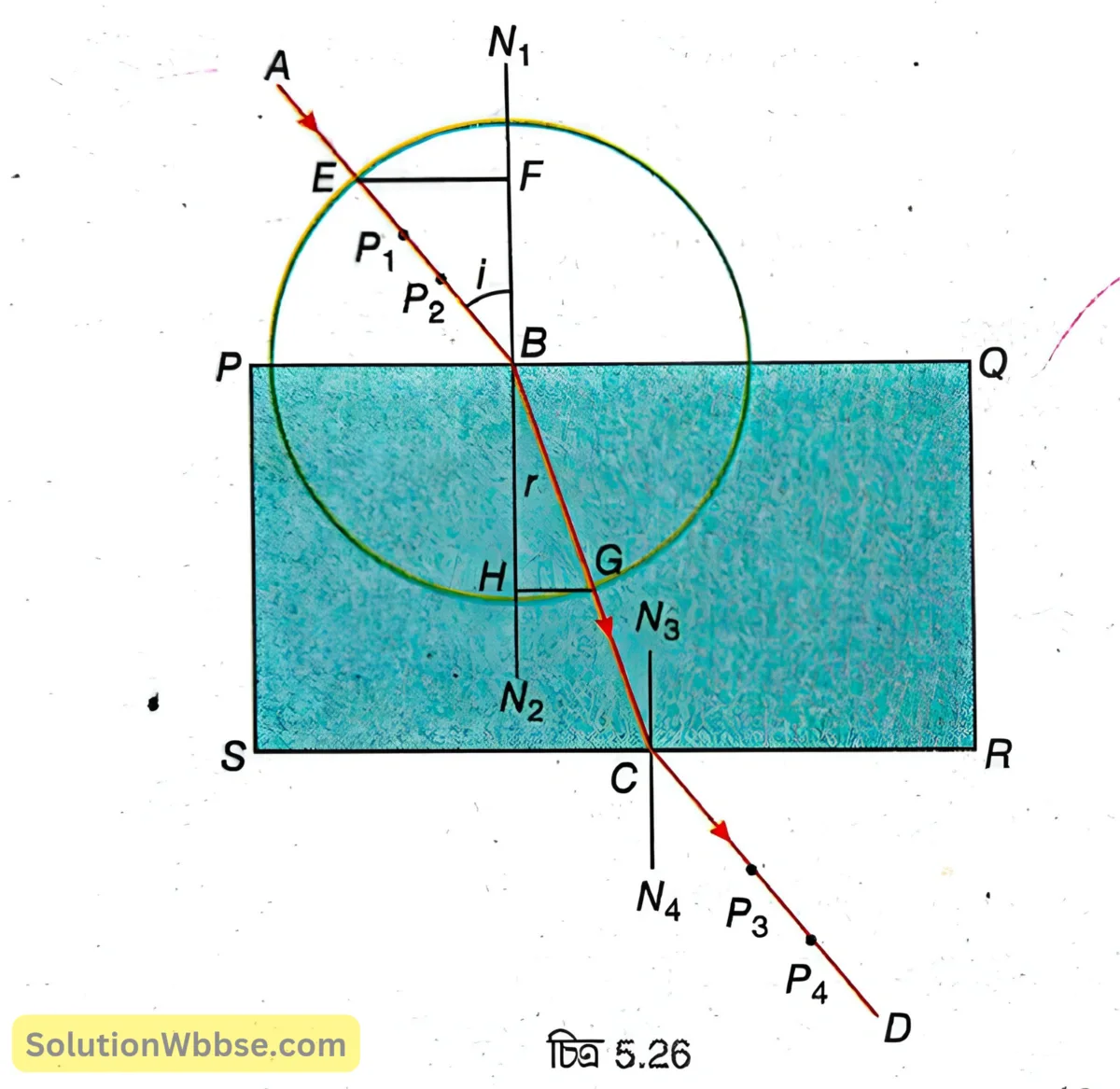
এবার \( B \) বিন্দুকে কেন্দ্র করে \( AB \) –এর তুলনায় কম ব্যাসার্ধ নিয়ে একটি বৃত্ত অঙ্কন করা হল। বৃত্তটি \( AB \) ও \( BC \) –কে যথাক্রমে \( E \) ও \( G \) বিন্দুতে ছেদ করে। \( E \) ও \( G \) থেকে \( N_1N_2 \) –এর ওপর যথাক্রমে \( EF \) ও \( GH \) লম্ব টানা হল এবং স্কেলের সাহায্যে \( EF,BE,GH \) ও \( BG \) –এর দৈর্ঘ্য পরিমাপ করা হল। এখানে \( \sin\angle ABN_1=\frac{EF}{BE} \) এবং \( \sin\angle N_2BC=\frac{GH}{BG}\) । \( B \) বিন্দুতে আলোর প্রতিসরণের ক্ষেত্রে, \( \angle ABN_1 = i \) হল আপতন কোণ ও \( \angle N_2BC = r \) হল প্রতিসরণ কোণ। এবার \( \frac{\sin i}{\sin r} \) নির্ণয় করা হল। \( P_1 \) ও \( P_2 \) পিন দুটির অবস্থান পরিবর্তন করে অর্থাৎ \( PQ \) সরলরেখার সঙ্গে \( AB \) সরলরেখার নতি পরিবর্তন করে কয়েকবার \( \frac{\sin i}{\sin r} \) নির্ণয় করা হলো। দেখা গেল প্রতিক্ষেত্রে এই অনুপাতের মান সমান। তবে এই অনুপাতের মান দুটি নির্দিষ্ট মাধ্যম ও নির্দিষ্ট বর্ণের আলোর ক্ষেত্রে সমান। এটিই হল প্রতিসরণের দ্বিতীয় সূত্রের বক্তব্য।

কোনো মাধ্যমের প্রতিসরাঙ্ক বলতে কী বোঝ?

যখন কোনো আলোকরশ্মি একটি মাধ্যম থেকে অন্য মাধ্যমে প্রতিসৃত হয়, তখন আপতন কোণের sine ও প্রতিসরণ কোণের sine -এর অনুপাতকে প্রথম মাধ্যম সাপেক্ষে দ্বিতীয় মাধ্যমের প্রতিসরাঙ্ক বলা হয়। কোনো আলোকরশ্মির 1 নং মাধ্যম থেকে 2 নং মাধ্যমে প্রতিসরণের ক্ষেত্রে আপতন কোণ \( i \) ও প্রতিসরণ কোণ \( r \) হলে, \( \frac{\sin i}{\sin r}={}_1\mu_2, \) যেখানে \( {}_1\mu_2 \)​ হল ধ্রুবক; যাকে 1 নং মাধ্যম সাপেক্ষে 2 নং মাধ্যমের প্রতিসরাঙ্ক বলা হয়। তবে 1 নং মাধ্যম শূন্যস্থান হলে, ওই স্থানে কিছু লেখা হয় না; তখন মাধ্যমের প্রতিসরাঙ্ককে পরম প্রতিসরাঙ্ক বলা হয়।

STP -তে বায়ুর পরম, প্রতিসরাঙ্ক কত?

STP -তে বায়ুর পরম, প্রতিসরাঙ্ক 1.00029। তাই বায়ু সাপেক্ষে কোনো মাধ্যমের প্রতিসরাঙ্ককে ওই মাধ্যমের পরম প্রতিসরাঙ্ক হিসেবে ধরা হয়।

কোনো মাধ্যমের আলোকীয় ঘনত্ব ও ভৌত ঘনত্ব কি একই? উদাহরণসহ ব্যাখ্যা করো।

মনে করি, দুটি আলোকীয় মাধ্যমের বায়ু সাপেক্ষে প্রতিসরাঙ্ক যথাক্রমে μ₁ ও μ₂। যদি μ₁ > μ₂ হয় তাহলে প্রথম মাধ্যম হল ঘনতর মাধ্যম আবার μ₂ > μ₁​ হলে দ্বিতীয় মাধ্যম হল ঘনতর মাধ্যম। এর সঙ্গে পদার্থের ভৌত ঘনত্বের কোনো সম্পর্ক নেই। যেমন জল ও তার্পিন তেলের ভৌত ঘনত্ব যথাক্রমে 1 g/cm³ ও 0.87 g/cm³ এবং বায়ু সাপেক্ষে প্রতিসরাঙ্ক যথাক্রমে 1.33 ও 1.47। এক্ষেত্রে জলের ভৌত ঘনত্ব তার্পিন তেলের চেয়ে বেশি, কিন্তু আলোক সাপেক্ষে তার্পিন তেল ঘনতর মাধ্যম এবং জল লঘুতর মাধ্যম।

কয়েকটি পদার্থের বায়ু সাপেক্ষে প্রতিসরাঙ্ক

পদার্থ	প্রতিসরাঙ্ক	পদার্থ	প্রতিসরাঙ্ক	পদার্থ	প্রতিসরাঙ্ক
হিরে	2.42	বেনজিন	1.50	বরফ	1.31
কার্বন ডাইসালফাইড	1.63	গ্লিসারিন	1.47	CO₂	1.00045 (STP)
অ্যানিলিন	1.59	তার্পিন তেল	1.47	হিলিয়াম	1.000036 (STP)
ফ্লিন্ট কাচ	1.53-1.92	অ্যালকোহল	1.37	বায়ু	1.00029 (STP)
ক্রাউন কাচ	1.48-1.6	জল	1.33	H₂	1.00014 (STP)

কখন \( \frac{Sin\;i\;}{Sin\;r}={}_1\mu_2 \) সূত্রটি প্রযোজ্য হয় না?

আলোকরশ্মি দুই মাধ্যমের বিভেদতলে লম্বভাবে আপতিত হলে, \( \frac{Sin\;i\;}{Sin\;r}={}_1\mu_2 \) সূত্রটি প্রযোজ্য হয় না। এক্ষেত্রে দ্বিতীয় মাধ্যমে আলোকরশ্মির অভিমুখের কোনো পরিবর্তন হয় না, তবে দ্বিতীয় মাধ্যমে আলোকরশ্মির গতিবেগের পরিবর্তন হয়।

কোনো আলোকরশ্মি লঘু থেকে ঘন মাধ্যমে প্রবেশ করলে গতিবেগ, তরঙ্গদৈর্ঘ্য ও কম্পাঙ্কের কীরূপ পরিবর্তন হয়?

লঘু থেকে ঘন মাধ্যমে প্রবেশ করলে আলোকরশ্মির গতিবেগ ও তরঙ্গদৈর্ঘ্য হ্রাস পায়, কিন্তু কম্পাঙ্ক অপরিবর্তিত থাকে।

কোনো আলোকরশ্মি ঘন থেকে লঘু মাধ্যমে প্রবেশ করলে গতিবেগ, তরঙ্গদৈর্ঘ্য ও কম্পাঙ্কের কীরূপ পরিবর্তন হয়?

কোনো আলোকরশ্মি ঘন থেকে লঘু মাধ্যমে প্রবেশ করলে আলোকরশ্মির গতিবেগ ও তরঙ্গদৈর্ঘ্য বৃদ্ধি পায় কিন্তু কম্পাঙ্ক অপরিবর্তিত থাকে।

বায়ুতে \( \lambda\) তরঙ্গদৈর্ঘ্যের কোনো আলোকরশ্মি \(\mu\) প্রতিসরাঙ্কের কোনো মাধ্যমে প্রবেশ করলে তরঙ্গদৈর্ঘ্য কত হবে?

আলোর কম্পাঙ্ক \( \nu \) হলে শূন্যস্থানে আলোর বেগ, \( c=\nu\lambda \) …(1)

আলোকরশ্মির যখন প্রতিসরণ হয় তখন দ্বিতীয় মাধ্যমে আলোকরশ্মির গতিবেগ ও তরঙ্গদৈর্ঘ্যের পরিবর্তন হলেও কম্পাঙ্ক অপরিবর্তিত থাকে। দ্বিতীয় মাধ্যমে আলোর বেগ ও তরঙ্গদৈর্ঘ্য যথাক্রমে \( V \) ও \( \lambda_1 \) হলে,

\( V=\nu\lambda_1 \) …(2)

আবার, \( \mu=\frac cV \)
বা, \( \mu=\frac{\nu\lambda}{\nu\lambda_1} \)
বা, \( \mu=\frac\lambda{\lambda_1} \)
বা, \( \lambda_1=\frac\lambda\mu \)

কোনো আলোকরশ্মি \( \mu_1 \) প্রতিসরাঙ্কের কোনো মাধ্যম থেকে \( \mu_2 \) প্রতিসরাঙ্কের কোনো মাধ্যমে প্রবেশ করল। এই দুই মাধ্যমে আলোর তরঙ্গদৈর্ঘ্য যথাক্রমে \( \lambda_1 \) ও \( \lambda_2 \) হলে দেখাও \( \mu_1\lambda_1=\mu_2\lambda_2 \)

শূন্যস্থানে আলোর বেগ \( =c \), প্রথম মাধ্যমে আলোর বেগ \( =\nu_1 \) ও দ্বিতীয় মাধ্যমে আলোর বেগ \( =\nu_2 \) হলে,

\( \mu_1=\frac c{\nu_1} \)
বা, \( \mu_1\nu_1=c \) …………(1)
এবং \( \mu_2=\frac c{v_2} \)
বা, \( \mu_2\nu_2=c \) …………(2)

(1) ও (2) নং সমীকরণ তুলনা করে পাই,

\( \mu_1\nu_1=\mu_2\nu_2 \) ……(3)

আলোর কম্পাঙ্ক \( \nu \) হলে, \( \nu_1=\nu\lambda_1 \) ও \( \nu_2=\nu\lambda_2 \)

সুতরাং, (3) নং সমীকরণ থেকে পাই,
\( \mu_1\cdot\nu\lambda_1=\mu_2\cdot\nu\lambda_2 \)
বা, \( \mu_1\lambda_1=\mu_2\lambda_2 \) [প্রমাণিত]

একটি আলোকরশ্মি একটি সমান্তরাল কাচ ফলকের ওপর \( i \) কোণে আপতিত হলে প্রতিফলিত রশ্মি ও প্রতিসৃত রশ্মির মধ্যবর্তী কোণ হয় 90°। দেখাও যে, কাচের প্রতিসরাঙ্ক \( \mu=\tan i \)।

মনে করি, প্রতিসরণ কোণ = r।

চিত্রে AB হল আপতিত রশ্মি, BC হল প্রতিফলিত রশ্মি ও BD হল প্রতিসৃত রশ্মি।

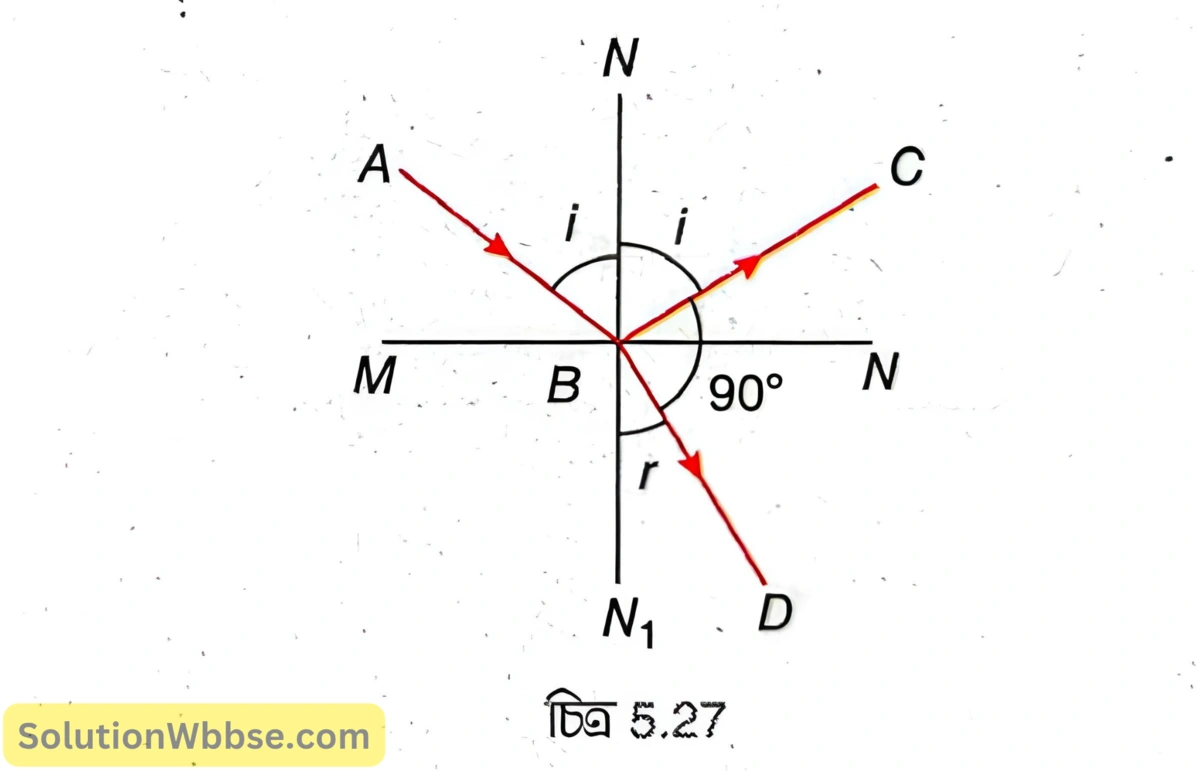
∴ \(\angle CBD=90^\circ \)

\( NN_1 \) হল \(B \) বিন্দুতে দুই মাধ্যমের বিভেদতলের ওপর অভিলম্ব।

∴\(\angle NBC+\angle CBD+\angle N_1BD=180^\circ \)
বা, \(i+90^\circ+r=180^\circ \)
বা, \(r=90^\circ-i\)

∴ \( B \) বিন্দুতে আলোর প্রতিসরণের ক্ষেত্রে, \( \frac{\sin i}{\sin r}=\mu \)
বা, \( \frac{\sin i}{\sin(90^\circ-i)}=\mu \)
বা, \( \frac{\sin i}{\cos i}=\mu \)
বা, \( \mu=\tan i \) [প্রমাণিত]

গ্লিসারিনের মধ্যে কাচদণ্ড ডোবালে তা আর দেখা যায় না কেন?

গ্লিসারিন ও কাচের প্রতিসরাঙ্ক প্রায় সমান, তাই কাচদণ্ডকে গ্লিসারিনের মধ্যে ডোবালে বিভেদতলে আলোকরশ্মির প্রতিফলন বা প্রতিসরণ হয় না বললেই চলে। তাই কাচদণ্ডকে বাইরে থেকে দেখা যায় না।

আয়তাকার কাচের স্ল্যাবে আলোর প্রতিসরণ ব্যাখ্যা করো এবং দেখাও স্ল্যাবের একপার্শ্বে কোনো রশ্মি আপতিত হয়ে স্ল্যাবের মধ্য দিয়ে গিয়ে যখন অপর পৃষ্ঠ থেকে নির্গত হবে তখন আপতিত রশ্মি ও নির্গত রশ্মি পরস্পরের সমান্তরাল হয়।

চিত্র 5.29 –এ একটি আয়তাকার কাচের স্ল্যাব দেখানো হয়েছে। এই স্ল্যাবের \( PQ\parallel SR \) এবং \( PS\parallel QR \)। এই আয়তাকার স্ল্যাবের \( PQ \) পার্শ্বের ওপর একটি আলোকরশ্মি \( AB \) তির্যকভাবে আপতিত হল। \( N_1N_2 \) হল \( B \) বিন্দুতে দুই মাধ্যমের বিভেদতলের ওপর অঙ্কিত অভিলম্ব। কাচ, বায়ু সাপেক্ষে ঘণতর মাধ্যম, তাই কাচ মাধ্যমে প্রতিসৃত রশ্মি \( BC \) অভিলম্বের দিকে বেঁকে যায়। \( B \) বিন্দুতে আলোর প্রতিসরণের ক্ষেত্রে, আপতন কোণ \( i_1=\angle ABN_1 \) ও প্রতিসরণ কোণ \( r_1=\angle N_2BC \)। \( BC \) রশ্মি কাচের মধ্য দিয়ে গিয়ে কাচ ও বায়ুর বিভেদতল \( SR \) -এ তির্যকভাবে \( C \) বিন্দুতে আপতিত হল এবং বায়ু মাধ্যমে \( CD \) পথে প্রতিসৃত হল। যেহেতু কাচ থেকে বায়ুতে অর্থাৎ ঘণতর থেকে লঘুতর মাধ্যমে আলো গেল, তাই CD রশ্মি অভিলম্ব \( N_3N_4 \) থেকে দূরে সরে যায়। \( C \) বিন্দুতে আলোর প্রতিসরণের ক্ষেত্রে, আপতন কোণ \( r_2=\angle BCN_3 \) ও প্রতিসরণ কোণ, \( i_2=\angle DCN_4 \)।

কাচের স্ল্যাবটি সমান্তরাল, তাই \( B \) ও \( C \) বিন্দুতে অভিলম্ব দুটিও সমান্তরাল হবে অর্থাৎ \( N_1N_2\parallel N_3N_4 \)।

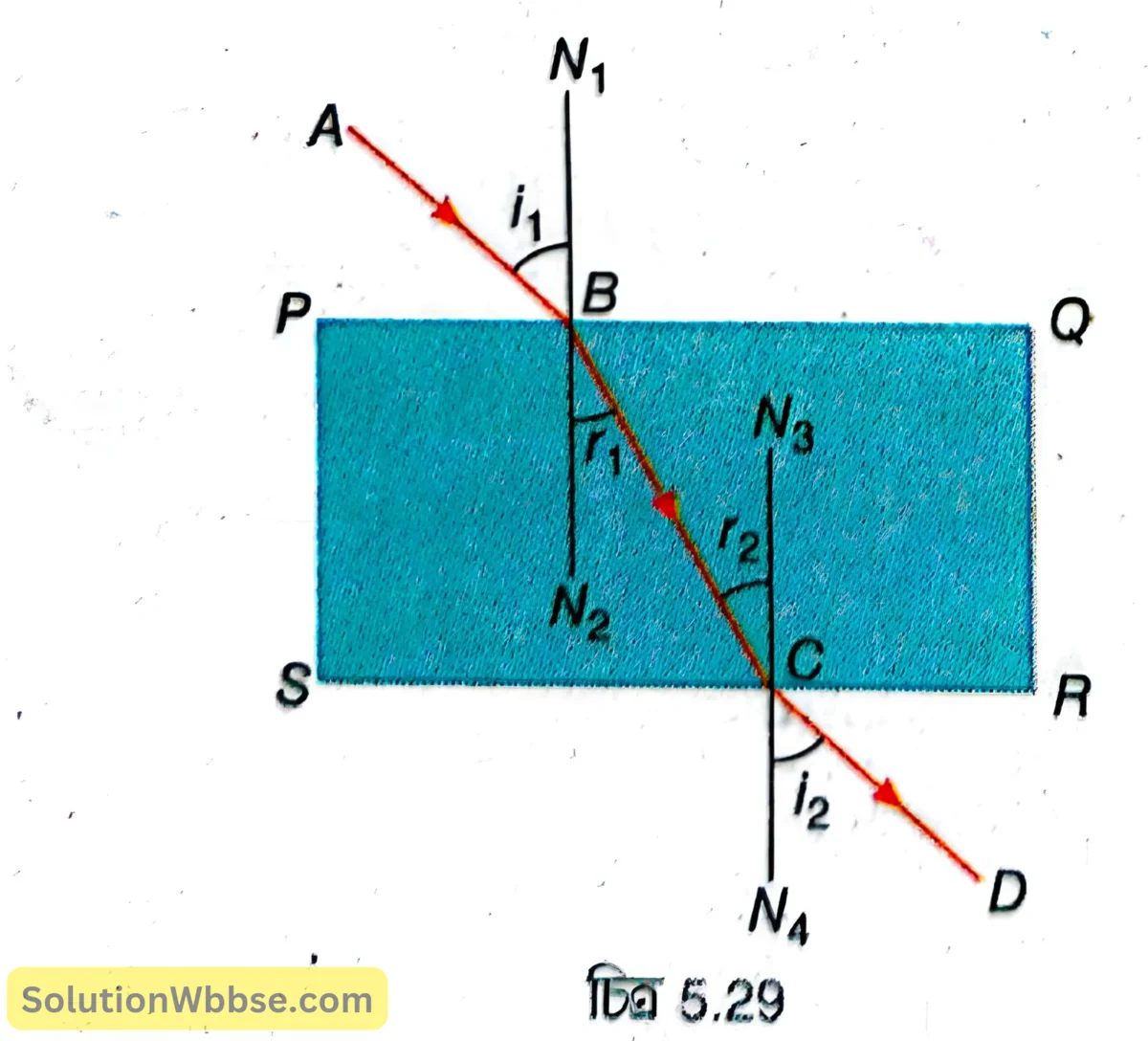
আবার \( N_1N_2\parallel N_3N_4 \), ভেদক \( BC \)।
সুতরাং, \( \angle N_2BC=\angle BCN_3 \) [একান্তর কোণ]
বা, \( r_1=r_2 \)

আলো প্রত্যাবর্তিতার নীতি মেনে চলে অর্থাৎ লঘু থেকে ঘন মাধ্যমে আলোর প্রতিসরণে আপতন কোণ যদি \( i \) ও প্রতিসরণ কোণ যদি \( r \) হয়, তাহলে ওই ঘন মাধ্যম থেকে লঘু মাধ্যমে আলো \( r \) কোণে আপতিত হলে প্রতিসরণ কোণ হবে \( i \)। সুতরাং, এক্ষেত্রে \( BC \) রশ্মি \( SR \) তলে \( r_1 \) কোণে আপতিত হলে বায়ু মাধ্যমে প্রতিসরণ কোণ হবে \( i_1 \)।

সুতরাং, \( i_2=i_1 \) অর্থাৎ \( AB\parallel CD \) হবে।

একটি প্রিজম এঁকে নিম্নলিখিত অংশগুলি বুঝিয়ে দাও – প্রতিসারক তল, প্রান্তরেখা, ভূমি, প্রধান ছেদ, প্রতিসারক কোণ।

প্রতিসারক তল – চিত্র 5.31 –এ একটি ত্রিভুজাকার প্রিজম দেখানো হয়েছে। এটি একটি স্বচ্ছ প্রতিসারক মাধ্যমের অংশবিশেষ। এই প্রিজমের \( DEF \) ও \( GHI \) তল দুটি ত্রিভুজাকার ও \( DEHG \), \( DFIG \) ও \( EFIH \) তল তিনটি আয়তাকার। এই তিনটি আয়তাকার তলের মধ্যে \( DEHG \) ও \( DFIG \) তল দুটি দিয়ে আলো প্রিজমের মধ্যে প্রবেশ করতে ও নির্গত হতে পারে। তাই এই তল দুটিকে প্রিজমের প্রতিসারক তল বলা হয়।

প্রান্তরেখা – প্রতিসারক তল দুটি যে সরলরেখা বরাবর মিলিত হয়, তাকে প্রিজমের প্রান্তরেখা বলে। এখানে \( DG \) হল প্রান্তরেখা।

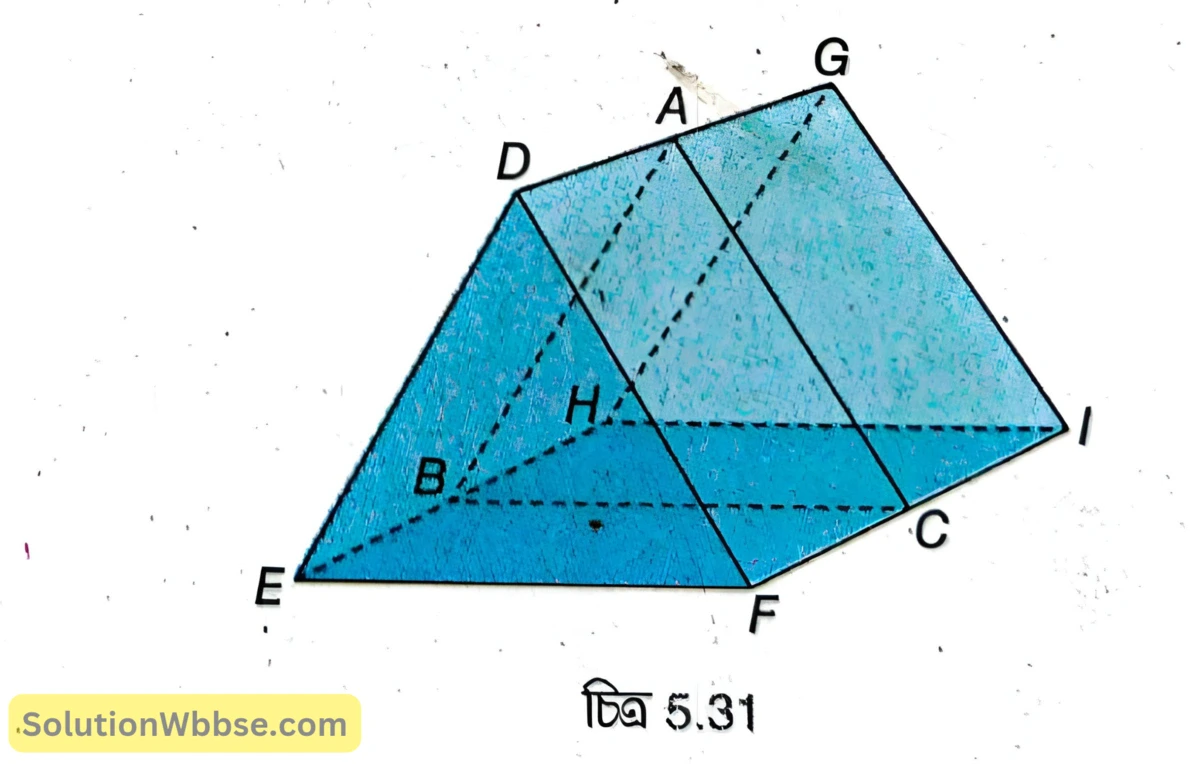
ভূমি – প্রান্তরেখার বিপরীত দিকের আয়তাকার তলকে ভূমি বলা হয়। এখানে \( EFIH \) হল ভূমি।

প্রধান ছেদ – প্রিজমের প্রান্তরেখার সঙ্গে সমকোণে কোনো সমতল কল্পনা করলে ওই সমতল প্রিজমকে একটি ত্রিভুজাকৃতি সমতলে ছেদ করে। একে প্রিজমের প্রধান ছেদ বলা হয়। এখানে \( ABC \) হল প্রিজমের প্রধান ছেদ।

প্রতিসারক কোণ – প্রিজমের প্রতিসারক তল দুটির মধ্যবর্তী কোণকে প্রিজমের প্রতিসারক কোণ বলা হয়। এখানে \( \angle BAC \) হল প্রিজমের প্রতিসারক কোণ।

একটি প্রিজমের প্রধান ছেদ বরাবর আলোর প্রতিসরণ রশ্মিচিত্রের সাহায্যে ব্যাখ্যা করো।

5.32 নং চিত্রে \( ABC \) হল একটি প্রিজমের প্রধান ছেদ, যার \( A \) হল প্রতিসারক কোণ ও \( BC \) হল ভূমি এবং \( AB \) ও \( AC \) হল দুটি প্রতিসারক তল। \( PQ \) আলোকরশ্মি \( AB \) প্রতিসারক তলের \( Q \) বিন্দুতে তির্যকভাবে \( i_1 \) কোণে আপতিত হয়েছে। এখানে আলোকরশ্মি লঘুতর (বায়ু) মাধ্যম থেকে ঘনতর (কাচ) মাধ্যমে প্রবেশ করে তাই প্রিজমের মধ্যে প্রতিসৃত রশ্মি \( QR \) অভিলম্ব \( MT \) -এর দিকে বেঁকে যায় এবং প্রতিসরণ কোণ হয় \( \angle RQT=r_1 \)। \( QR \) আলোক রশ্মি প্রিজমের মধ্য দিয়ে গিয়ে \( AC \) প্রতিসারক তলে \( R \) বিন্দুতে আপতিত হয়। এখানে আলোকরশ্মি ঘনতর (কাচ) মাধ্যম থেকে লঘুতর (বায়ু) মাধ্যমে প্রবেশ করে তাই বায়ুতে প্রতিসৃত রশ্মি \( RS \) অভিলম্ব \( NT \) থেকে দূরে সরে যায়। \( R \) বিন্দুতে আলোর প্রতিসরণে আপতন কোণ \( \angle QRT=r_2 \) এবং প্রতিসরণ কোণ, \( \angle NRS=i_2 \)।

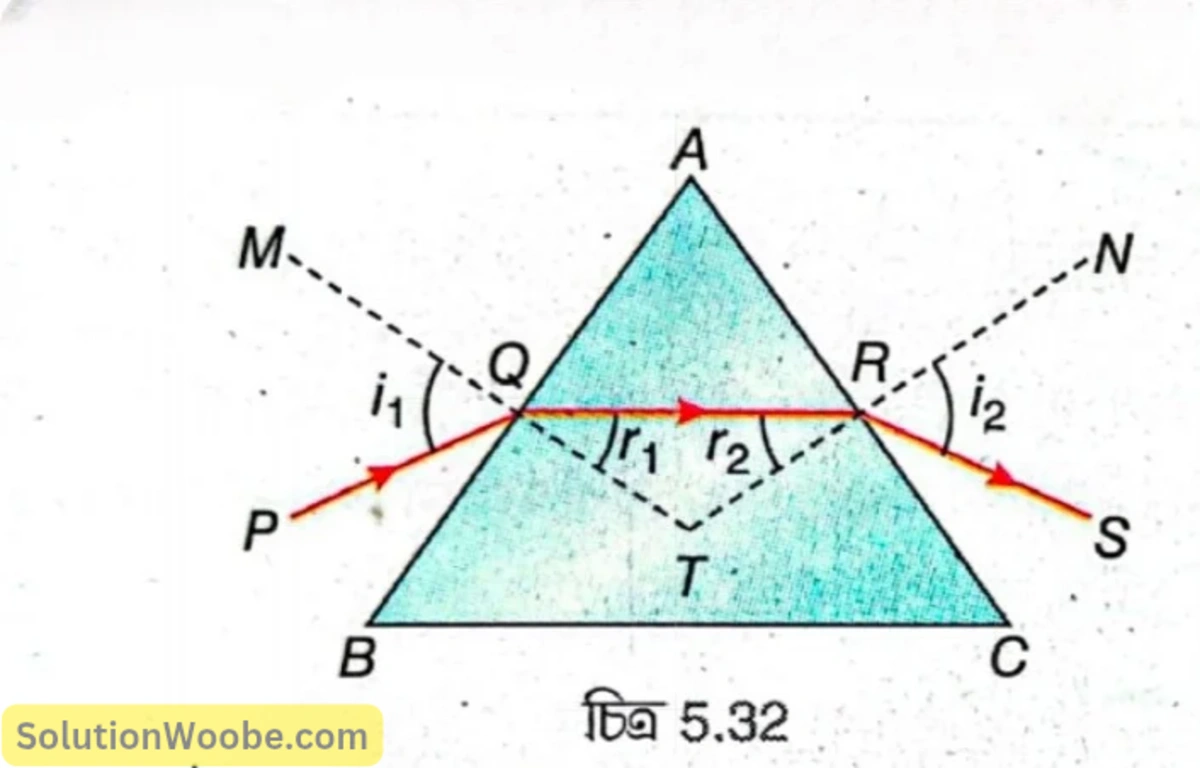
প্রিজমের প্রধান ছেদ বরাবর আলোর প্রতিসরণে দেখাও চ্যুতিকোণ, \( \delta = i_1 + i_2 – A; \) যেখানে, \( i_1 \) হল আপতন কোণ, \( i_2 \) হল নির্গম কোণ ও A হল প্রিজমের প্রতিসারক কোণ।

5.33 নং চিত্রে ABC হল A প্রতিসারক কোণ ও μ প্রতিসরাঙ্কযুক্ত একটি প্রিজমের প্রধান ছেদ যার BC ভূমি, AB ও AC দুটি প্রতিসারক তলকে নির্দেশ করে। PQRS হল প্রিজমের মধ্য দিয়ে আলোর প্রতিসরণে আলোর গতিপথ। AB তলে আলোর প্রতিসরণে আপতন কোণ, \( \angle PQM=i_1 \) ও প্রতিসরণ কোণ, \( \angle PQT=r_1 \)।

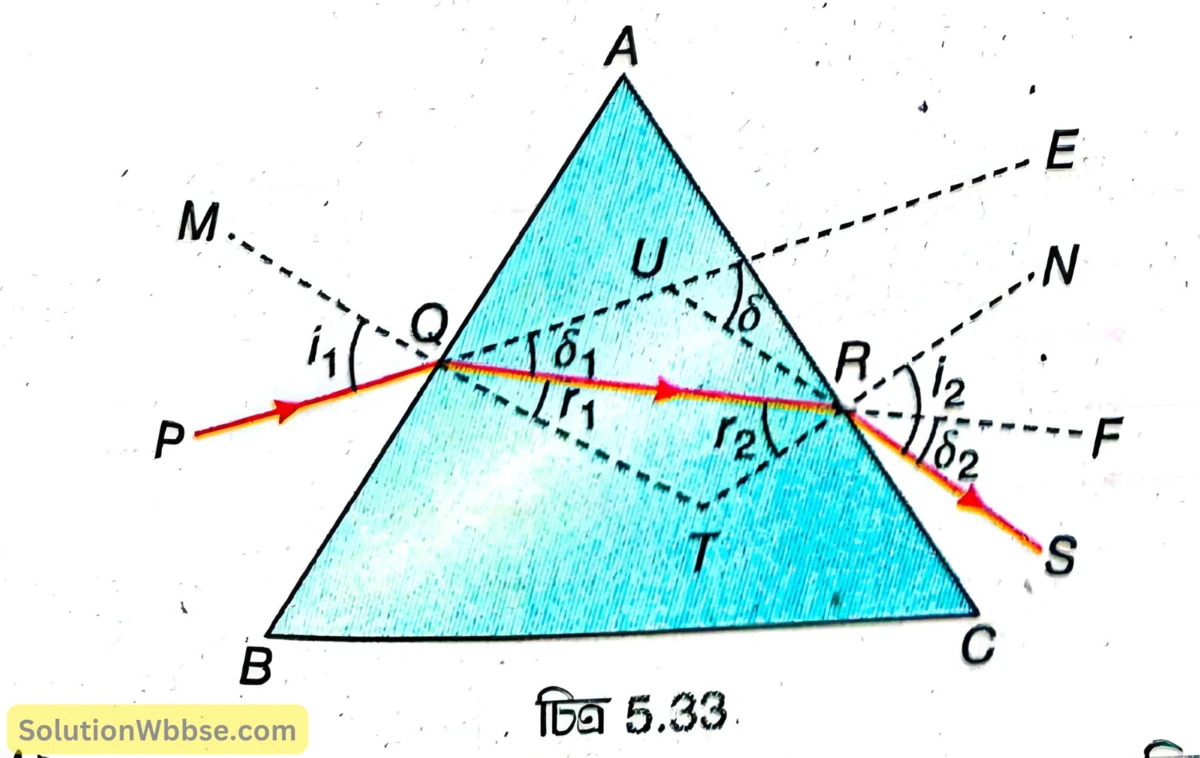
AB তলে আলোর প্রতিসরণে চ্যুতিকোণ, \( \delta_1 = \angle EQR = i_1 – r_1 \)।

AC তলে QR আপতিত রশ্মির ক্ষেত্রে আপতন কোণ, \( \angle QRT = r_2 \) ও প্রতিসরণ কোণ \( \angle NRS = i_2 \)

∴ চ্যুতিকোণ, \( \delta_2 = \angle NRF = i_2 – r_2 \)

PQ হল প্রিজমে আপতিত রশ্মি এবং RS নির্গম রশ্মি। SR -কে পিছন দিকে বাড়ালে বর্ধিত SR, PE -কে U বিন্দুতে ছেদ করে। সুতরাং, আলোকরশ্মির Q ও R দুটি বিন্দুতে প্রতিসরণ হওয়ার জন্য চ্যুতিকোণ হয়, \( \angle EUR = \delta \)

\( \triangle UQR \) –এর \( \angle EUR \) হল বহিস্থ কোণ।
∴ \( \angle EUR = \angle UQR + \angle QRU \)
বা, \( \angle EUR = \angle UQR + \angle FRS \) [ ∵\( \angle QRU = \angle FRS \) (বিপ্রতীপ কোণ)]
বা, \( \delta = \delta_1 + \delta_2 \)
বা, \( \delta = i_1 – r_1 + i_2 – r_2 \)
বা, \( \delta = i_1 + i_2 – (r_1 + r_2) \) …………… (1)

∆QTR থেকে পাই, \( r_1 + r_2 + \angle QTR = 180^\circ \) …………… (2)
আবার চতুর্ভুজ AQTR – এর \( \angle AQT + \angle ART = 90^\circ + 90^\circ = 180^\circ \)
∴ \( \angle QAR + \angle QTR = 360^\circ – 180^\circ = 180^\circ \) …………… (3)

(2) নং ও (3) নং সমীকরণ তুলনা করে পাই,

\( \angle QAR = r_1 + r_2 \)

বা, \( A = r_1 + r_2 \)

∴ (1) নং সমীকরণ থেকে পাই, চ্যুতিকোণ, \( \delta = i_1 + i_2 – A \)

প্রিজমের প্রধান ছেদ বরাবর আলোর প্রতিসরণে চ্যুতিকোণ, \( \delta=i_1+i_2-A \) যেখানে \( i_1 \) হল আপতন কোণ, \( i_2 \) হল নির্গম কোণ ও \( A \) হল প্রতিসারক কোণ। দেখাও আপতন কোণ যদি \( i_2 \) হত তাহলে চ্যুতিকোণ অপরিবর্তিত থাকত।

মনে করি, \( AB \) তলে আপতন কোণ \( i_1 \) হলে প্রতিসরণ কোণ হয় \( r_1 \) ও \( AC \) তলে আপতন কোণ হয় \( r_2 \)।

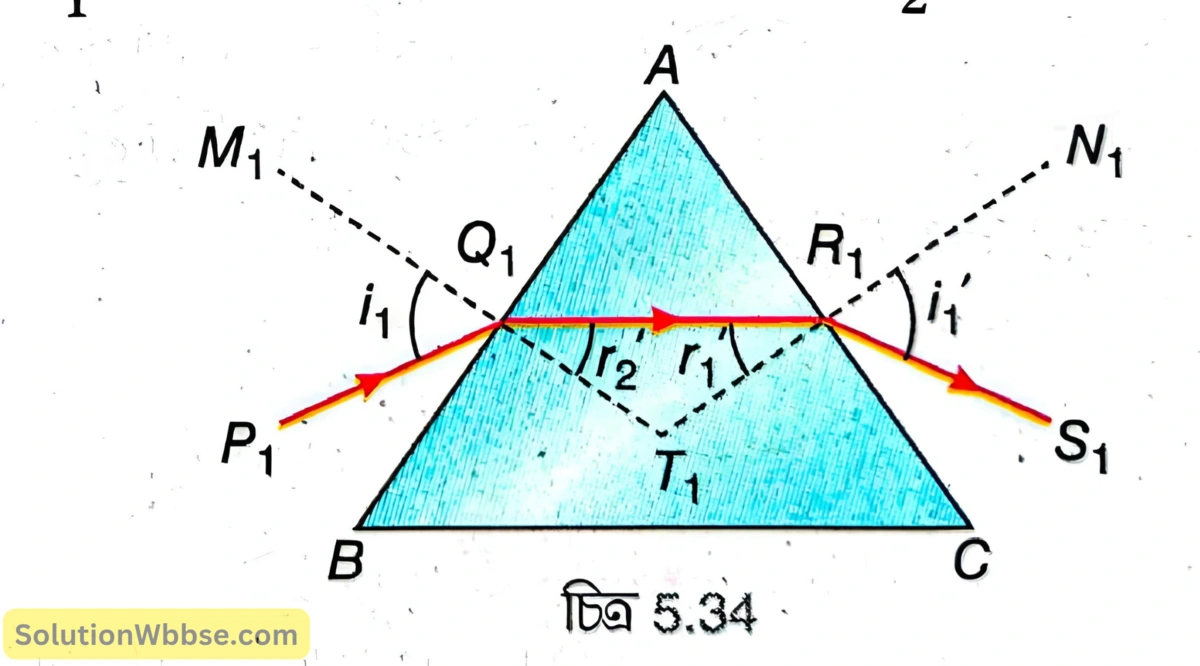
এখন AB তলে আপতন কোণ i₂ হলে যদি প্রতিসরণ কোণ \(r_2′\) হয় তাহলে আলোর প্রত্যাবর্তিতার নীতি অনুযায়ী, \(r_2’=r_2\) হবে।

AC তলে আপতন কোণ \(r_2′\) হলে \(r_1’+r_2’=A \)
বা, \(r_1’+r_2=A \)
বা, \(r_1’=A-r_2 \)
বা, \(r_1’=r_1 \)

\( R_1 \) বিন্দুতে আলোর প্রতিসরণে প্রতিসরণ কোণ \( i_1\)‘ হলে আলোর প্রত্যাবর্তিতার নীতি অনুযায়ী, \( i_1’=i_1 \)।

∴ চ্যুতিকোণ, \( \delta\)‘\(=i_2+i_1′-A \)
বা, \( \delta\)‘\(=i_2+i_1-A \)
বা, \( \delta\)‘\(=\delta \) [প্রমাণিত]

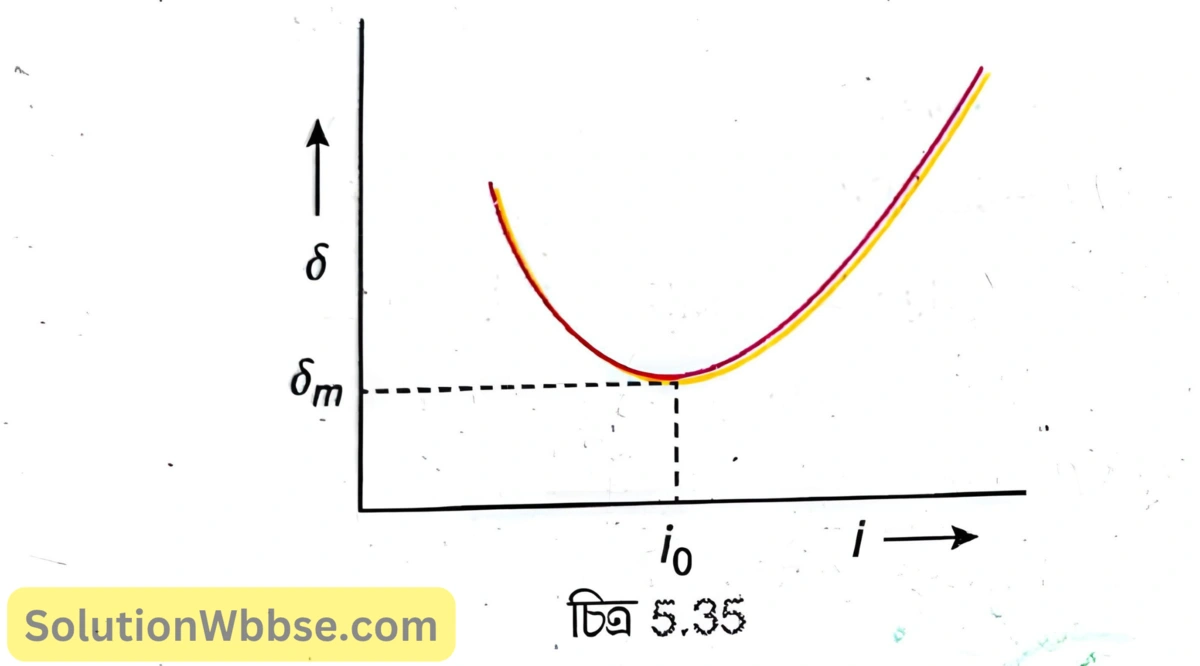
প্রিজমের জন্য \( i-\delta \) লেখচিত্র আঁকো ও ব্যাখ্যা করো।

কোনো নির্দিষ্ট প্রিজমের জন্য (A = ধ্রুবক) আপতন কোণ পরিবর্তন করলে চ্যুতিকোণেরও পরিবর্তন হয়। এখন আপতিত রশ্মিকে অপরিবর্তিত রেখে প্রিজমকে ঘোরালে আপতন কোণের পরিবর্তন হয়। দেখা যায় আপতন কোণের মান বাড়াতে থাকলে প্রথমে চ্যুতিকোণ কমতে থাকে এবং আপতন কোণের একটি নির্দিষ্ট মানে \( \left(i_0\right) \) চ্যুতিকোণ ন্যূনতম \( \left(\delta_m\right) \) হয়। আপতন কোণের মান এরপর আরও বাড়াতে থাকলে চ্যুতিকোণ ক্রমশ বাড়তে থাকে। 5.35 নং চিত্রে আপতন কোণের পরিবর্তনের সঙ্গে চ্যুতিকোণের পরিবর্তন দেখানো হয়েছে।

প্রিজমের মধ্য দিয়ে আলোকরশ্মির প্রতিসরণে চ্যুতিকোণ ন্যূনতম হওয়ার শর্ত কী? এক্ষেত্রে প্রিজমের মধ্য দিয়ে আলোকরশ্মির গতিপথ চিত্রের সাহায্যে দেখাও।

কোনো প্রিজমের প্রতিসারক কোণ \( =A \), আপতন কোণ \( =i_1 \) নির্গমন কোণ \( =i_2 \) হলে চ্যুতিকোণ, \( \delta=i_1+i_2-A \)

প্রথম প্রতিসারক তলে আলোর প্রতিসরণে প্রতিসরণ কোণ = \( r_1 \) ও দ্বিতীয় প্রতিসারক তলে আলোর আপতন কোণ = \( r_2 \) হলে \( A=r_1+r_2 \)।

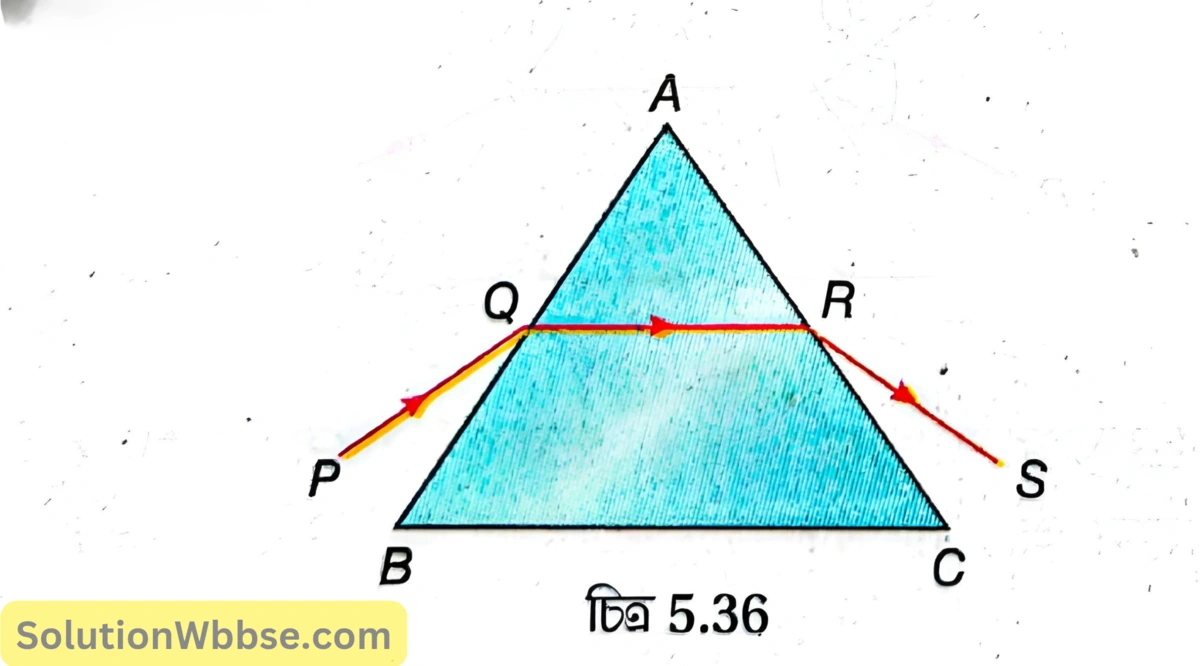
চ্যুতিকোণ ন্যূনতম হওয়ার শর্ত হল, \( i_1=i_2 \) ও \( r_1=r_2 \)। চ্যুতিকোণ ন্যূনতম হলে প্রিজমের মধ্য দিয়ে আলোকরশ্মির গতিপথ ভূমির সমান্তরাল হবে অর্থাৎ \( QR\parallel BC \) হবে [চিত্র 5.36]।

কোনো প্রিজমের ভূমির সমান্তরালভাবে আপতিত রশ্মির প্রতিসরণ রশ্মিচিত্রের সাহায্যে ব্যাখ্যা করো।

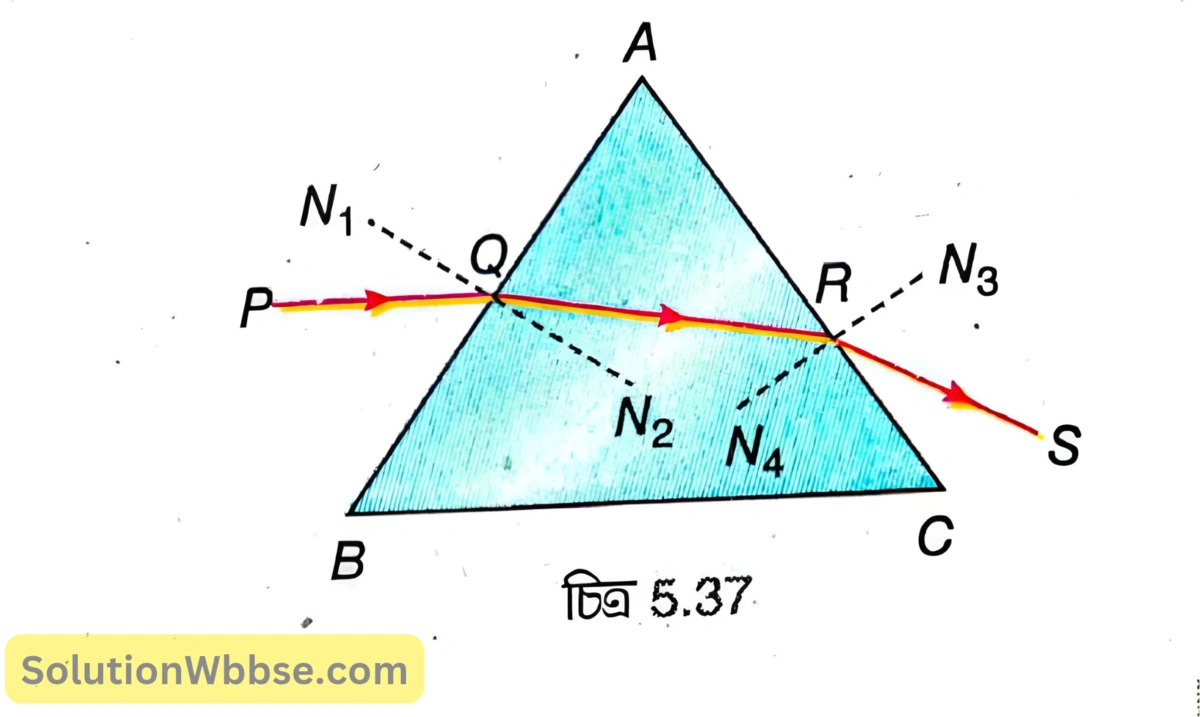
চিত্র 5.37 -এ \( ABC \) হল একটি প্রিজমের প্রধান ছেদ যার \( A \) হল প্রতিসারক কোণ ও \( BC \) হল ভূমি। \( PQ \) আলোকরশ্মি প্রিজমের \( AB \) প্রতিসারক তলে \( Q \) বিন্দুতে আপতিত হয়ে অভিলম্ব \( N_1N_2 \) -এর দিকে বেঁকে যায় এবং প্রিজমের মধ্য দিয়ে গিয়ে \( AC \) প্রতিসারক তলে \( R \) বিন্দুতে আপতিত হয় এবং বায়ু মাধ্যমে প্রতিসৃত রশ্মি \( RS \) অভিলম্ব \( N_3N_4 \) -এর থেকে দূরের দিকে সরে যায়। এই \( RS \) রশ্মি প্রিজমের ভূমির দিকে বেঁকে যায়। সুতরাং, কোনো প্রিজমের ভূমির সমান্তরালভাবে আপতিত রশ্মি প্রিজম থেকে নির্গত হওয়ার পর ভূমির দিকে বেঁকে যায়।

লেন্স

লেন্স কাকে বলে? লেন্স কয় প্রকার ও কী কী?

লেন্স হল দুটি গোলীয় তল বা একটি গোলীয় ও একটি সমতল দ্বারা সীমাবদ্ধ স্বচ্ছ প্রতিসারক মাধ্যম। লেন্স সাধারণত দু-প্রকার –

1. উত্তল লেন্স
2. অবতল লেন্স।

উত্তল লেন্স ও অবতল লেন্স কাকে বলে?

উত্তল লেন্স – যে লেন্সের মাঝের অংশটি মোটা ও প্রান্তের দিক ক্রমশ সরু তাকে উত্তল লেন্স বলা হয়।

অবতল লেন্স – যে লেন্সের মাঝের অংশটি সরু ও প্রান্তের দিক ক্রমশ মোটা তাকে অবতল লেন্স বলা হয়।

উত্তল লেন্সকে অভিসারী লেন্স ও অবতল লেন্সকে অপসারী লেন্স বলা হয় কেন?

বায়ুতে থাকা একটি উত্তল লেন্সের ওপর সমান্তরাল রশ্মিগুচ্ছ আপতিত হলে প্রতিসরণের পর তা অভিসারী রশ্মিগুচ্ছে পরিণত হয়, তাই উত্তল লেন্সকে অভিসারী লেন্স বলা হয় [চিত্র 5.38 (a)]।

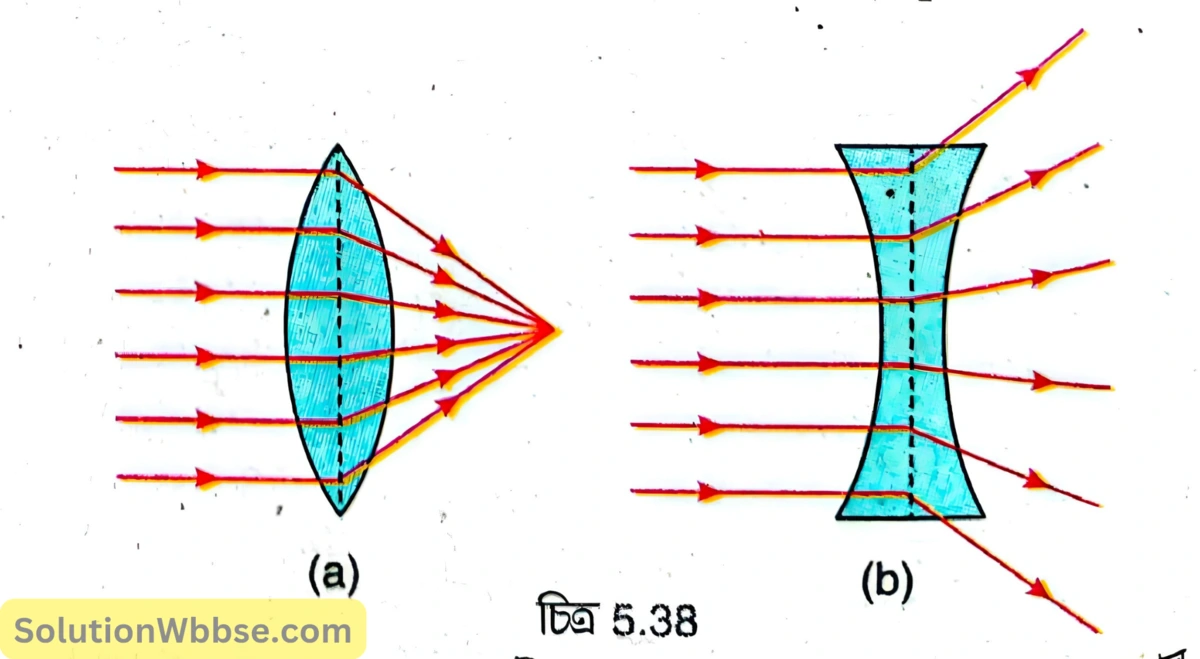
আবার বায়ুতে থাকা একটি অবতল লেন্সের ওপর সমান্তরাল রশ্মিগুচ্ছ আপতিত হলে প্রতিসরণের পর তা অপসারী রশ্মিগুচ্ছে পরিণত হয়, তাই অবতল লেন্সকে অপসারী লেন্স বলা হয় [চিত্র 5.38 (b)]।

চিত্রসহ সংজ্ঞা লেখো – লেন্সের (i) বক্তৃতা কেন্দ্র (ii) বক্রতা ব্যাসার্ধ (iii) প্রধান অক্ষ।

বক্রতা কেন্দ্র – একটি লেন্সের কোনো গোলীয় তল যে গোলকের অংশ তার কেন্দ্রকে বক্রতা কেন্দ্র বলা হয়।

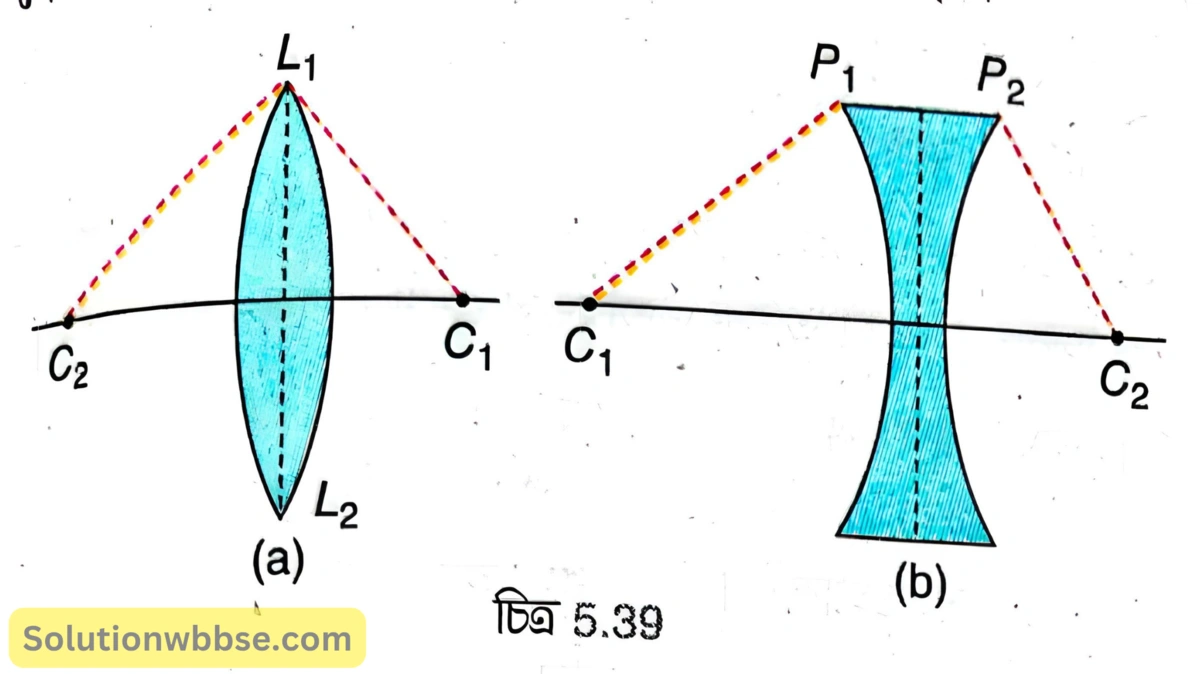
5.39 (a) ও (b) নং চিত্রে যথাক্রমে উত্তল লেন্স ও অবতল লেন্সের বামদিকের ও ডানদিকের গোলীয় তল দুটির বক্রতা কেন্দ্র যথাক্রমে \( C_1 \) ও \( C_2 \)।

বক্তৃতা ব্যাসার্ধ – একটি লেন্সের কোনো গোলীয় তল যে গোলকের অংশ তার ব্যাসার্ধকে ওই তলের বক্রতা ব্যাসার্ধ বলা হয়। 5.39 (a) নং চিত্রে \( C_1L_1 \) ও \( C_2L_1 \) হল যথাক্রমে উত্তল লেন্সের বামদিক ও ডানদিকের গোলীয় তলের বক্রতা ব্যাসার্ধ এবং 5.39 (b) নং চিত্রে \( C_1P_1 \) ও \( C_2P_2 \) হল অবতল লেন্সের বামদিক ও ডানদিকের গোলীয় তলের বক্রতা ব্যাসার্ধ।

প্রধান অক্ষ – কোনো লেন্সের দুটি তল গোলীয় হলে লেন্সটির বক্রতা কেন্দ্র দুটির সংযোজী সরলরেখাকে ওই লেন্সের প্রধান অক্ষ বলা হয়।

5.39 (a) ও (b) নং চিত্রে \( C_1C_2 \) হল যথাক্রমে উত্তল ও অবতল লেন্সের প্রধান অক্ষ।

চিত্রসহ সংজ্ঞা লেখো – লেন্সের আলোককেন্দ্র।

যদি কোনো আলোকরশ্মি কোনো লেন্সের একটি তলে আপতিত হয়ে লেন্সের মধ্য দিয়ে গিয়ে অন্য তল থেকে নির্গত হওয়ার সময় আপতিত রশ্মির সঙ্গে সমান্তরালভাবে নির্গত হয়, তাহলে লেন্সের মধ্য দিয়ে যাওয়ার সময় আলোকরশ্মি প্রধান অক্ষকে যে বিন্দুতে ছেদ করে তাকে লেন্সের আলোককেন্দ্র বলা হয়।

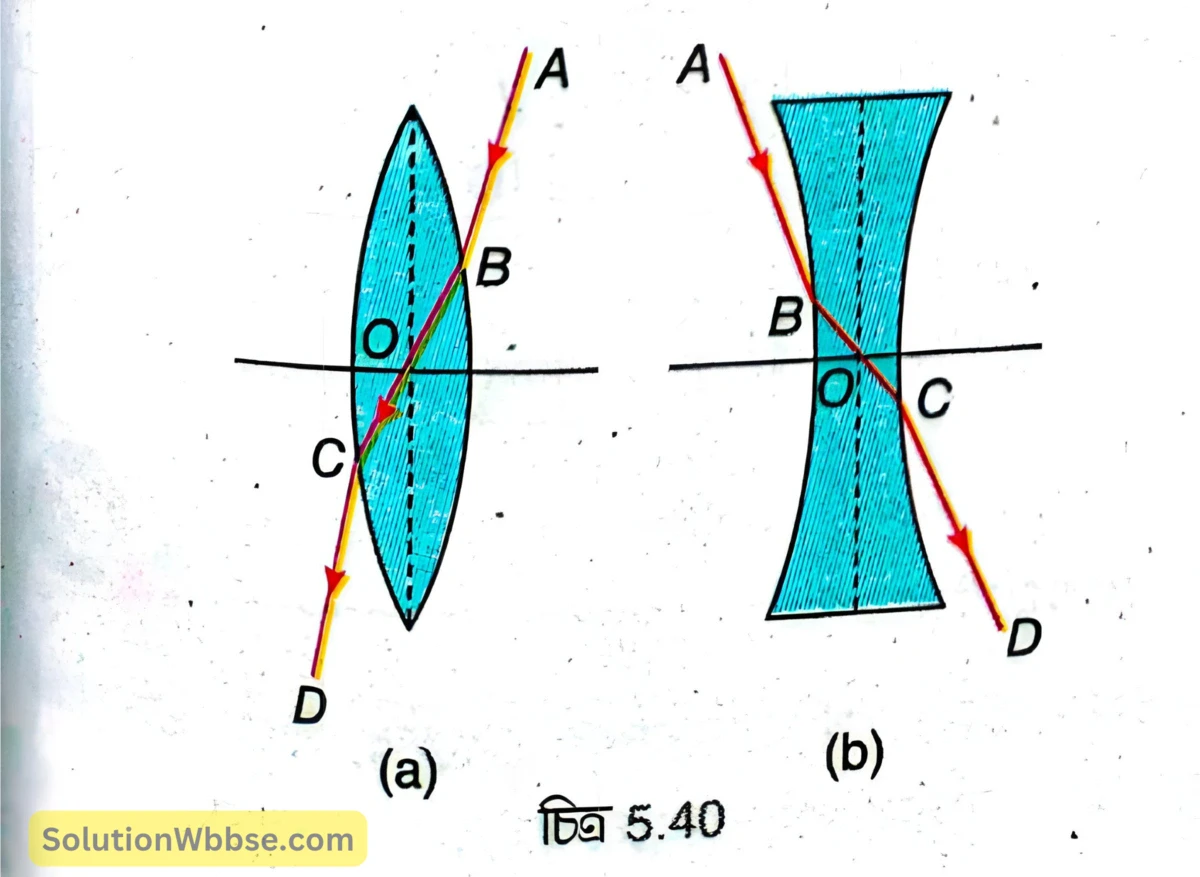
5.40 (a) ও (b) নং চিত্রে যথাক্রমে একটি উত্তল ও অবতল লেন্সের ওপর \( AB \) হল আপতিত রশ্মি ও \( CD \) হল নির্গম রশ্মি এবং \( AB\parallel CD \)। এই অবস্থায় \( BC \) রশ্মি লেন্সের মধ্য দিয়ে যাওয়ার সময় প্রধান অক্ষকে \( O \) বিন্দুতে ছেদ করে। \( O \) হল লেন্সের আলোককেন্দ্র।

দেখাও কোনো লেন্সের আলোককেন্দ্র একটি নির্দিষ্ট বিন্দু।

5.41 নং চিত্রে \( L_1L_2 \) একটি উত্তল লেন্স, যার \( XY \) হল প্রধান অক্ষ, \( C_1 \) ও \( C_2 \) হল যথাক্রমে বামদিক ও ডানদিকের গোলীয় তলের বক্রতা কেন্দ্র, \( O \) হল আলোককেন্দ্র।
∴ \( AA_1\parallel BB_1 \)

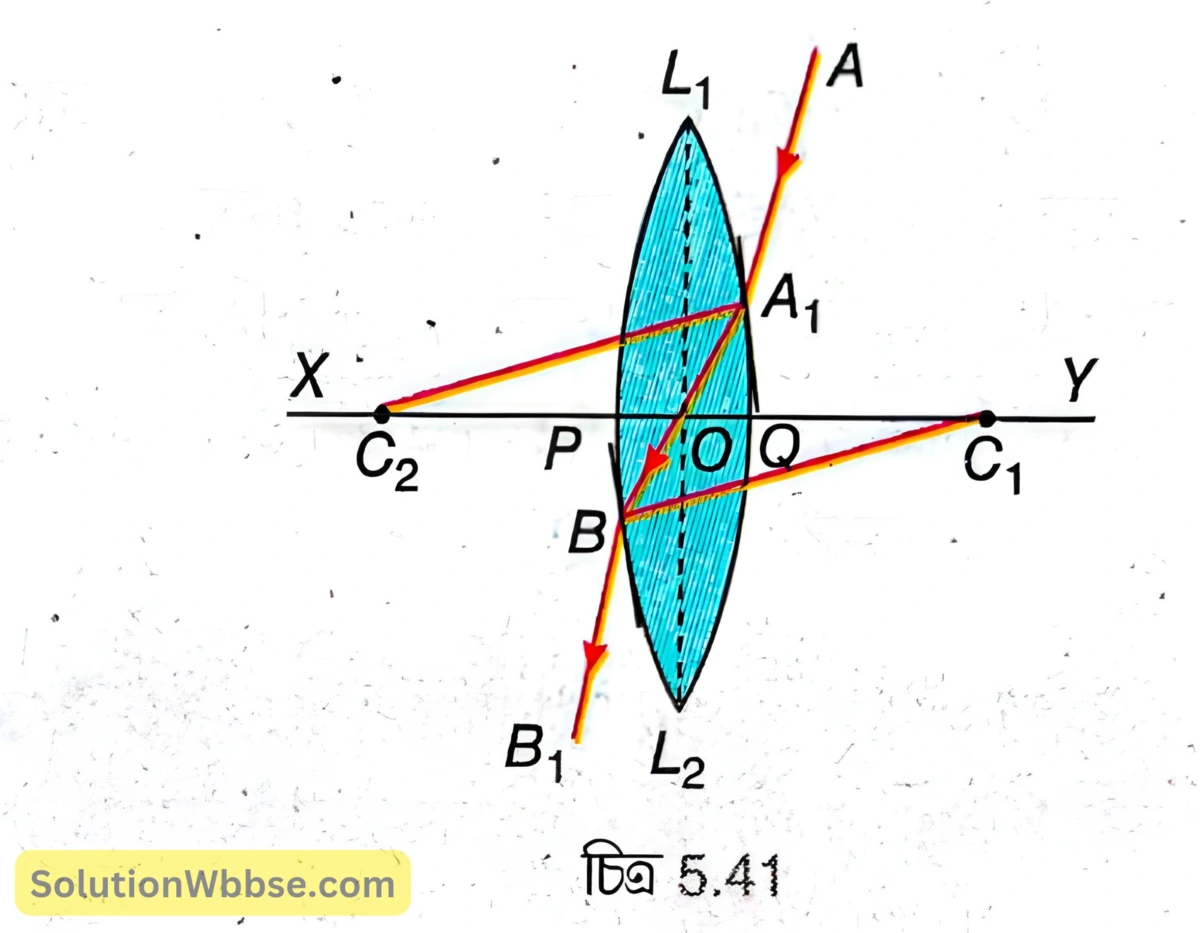
\( A_1C_2 \) ও \( C_1B \) হল যথাক্রমে ডান ও বাম গোলীয় তলের ওপর \( A_1 \) ও \( B \) বিন্দুতে অভিলম্ব বা বক্রতা ব্যাসার্ধ।

∴ \( A_1C_2\parallel C_1B \)
এখন \( \bigtriangleup A_1C_2O \) ও \( \bigtriangleup BC_1O \) -এর থেকে পাই, \( \angle A_1OC_2=\angle C_1OB \) [বিপ্রতীপ কোণ]
এবং \( \angle C_2A_1O=\angle OBC_1 \) [ \( A_1C_2\parallel C_1B \) ও \( A_1B \) ভেদক]

∴ \( \bigtriangleup A_1C_2O \) ও \( \bigtriangleup BC_1O \) সদৃশ।
∴ \( \frac{C_2O}{C_1O}=\frac{A_1C_2}{BC_1} \)

মনে করি, \( A_1C_2=r_1 \) ও \( BC_1=r_2 \)
∴ \( \frac{C_2O}{C_1O}=\frac{r_1}{r_2} \)

এখানে, \( r_1 \) ও \( r_2 \) হল যথাক্রমে \( L_1QL_2 \) ও \( L_1PL_2 \) গোলীয় তলের বক্রতা ব্যাসার্ধ, তাই \( \frac{C_2O}{C_1O} \) অনুপাতটি নির্দিষ্ট। এ ছাড়া \( C_1 \) ও \( C_2 \) নির্দিষ্ট বিন্দু। সুতরাং, \( O \) বা লেন্সের আলোককেন্দ্র নির্দিষ্ট বিন্দু।

পাতলা লেন্স কাকে বলে? পাতলা লেন্সের আলোককেন্দ্রের চিত্রসহ সংজ্ঞা লেখো।

পাতলা লেন্স – যে লেন্সের বেধ গোলীয় তলের বক্রতা ব্যাসার্ধের তুলনায় নগণ্য তাকে পাতলা লেন্স বলা হয়।

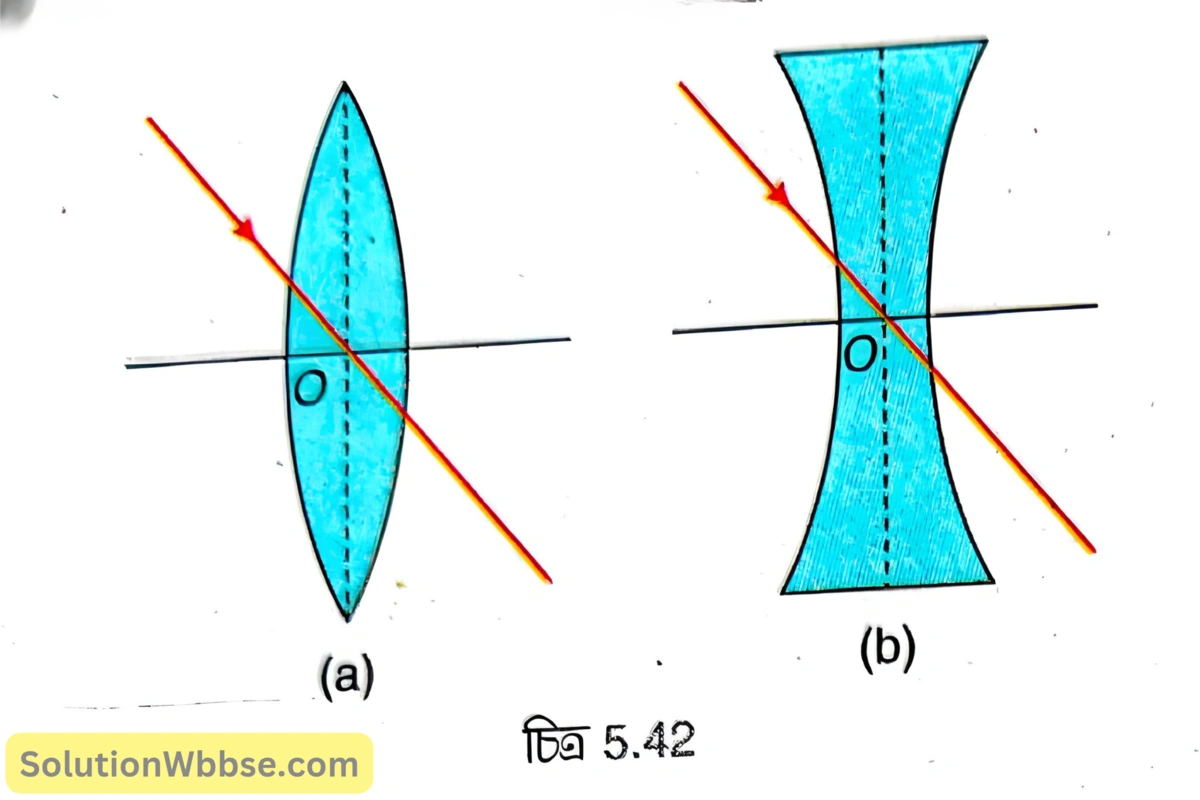
পাতলা লেন্সের আলোককেন্দ্র – পাতলা লেন্সের আলোককেন্দ্র হল প্রধান অক্ষের ওপর অবস্থিত এমন একটি বিন্দু যার মধ্য দিয়ে আলোকরশ্মি গেলে কোনোরকম চ্যুতি হয় না। 5.42 (a) ও (b) নং চিত্রে যথাক্রমে পাতলা উত্তল লেন্স ও পাতলা অবতল লেন্সের আলোককেন্দ্র হল \( O \)।

প্রতিসারক তল দ্বয়ের আকারের ভিত্তিতে উত্তল লেন্স কয় প্রকার ও কী কী? প্রত্যেক প্রকারের চিত্রসহ সংজ্ঞা লেখো।

প্রতিসারক তল দ্বয়ের আকারের ভিত্তিতে উত্তল লেন্স তিন ধরনের হতে পারে – উভোত্তল লেন্স, সমতলোত্তল লেন্স এবং অবতলোত্তল লেন্স।

উভোত্তল লেন্স – যে উত্তল লেন্সের উভয় প্রতিসারক তলই উত্তল তাকে উভোত্তল লেন্স বলা হয়।

সমতলোত্তল লেন্স – যে উত্তল লেন্সের একটি প্রতিসারক তল উত্তল ও অপর প্রতিসারক তল সমতল তাকে সমতলোত্তল লেন্স বলা হয়।

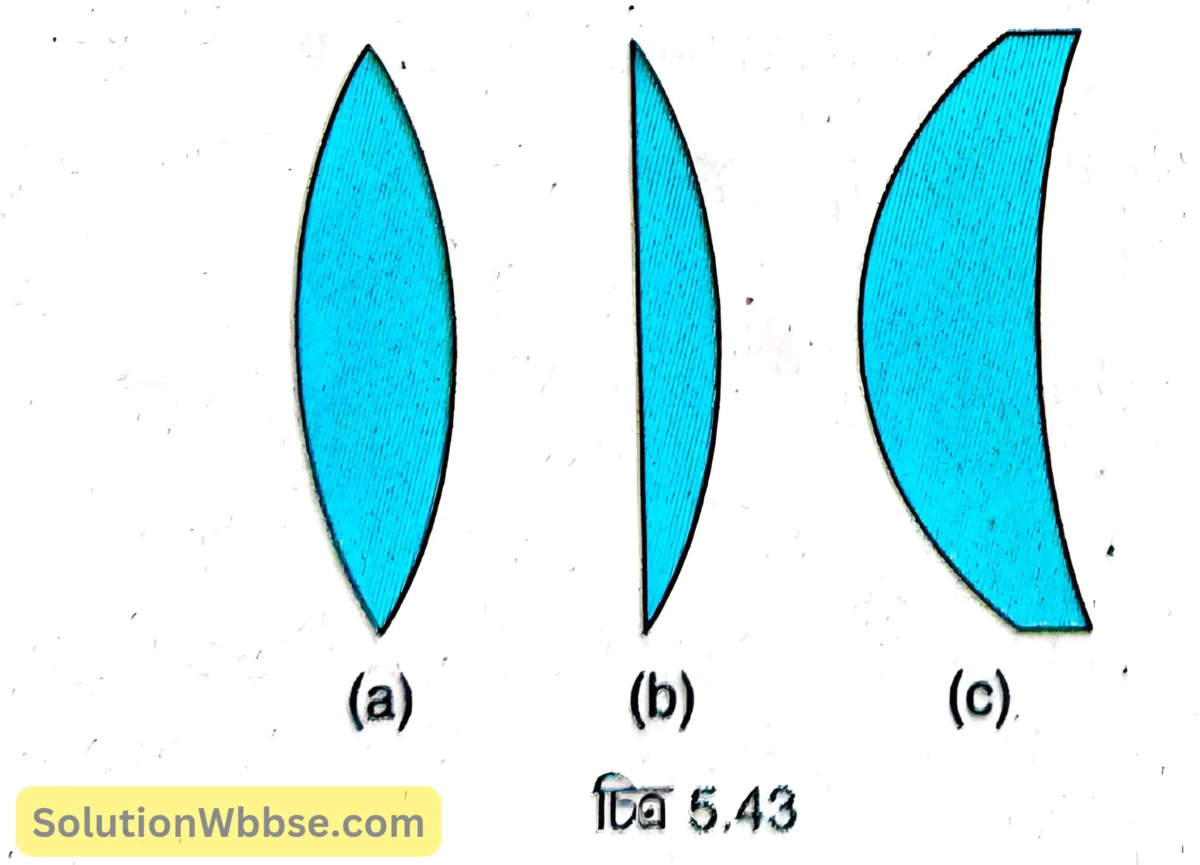
অবতলোত্তল লেন্স – যে উত্তল লেন্সের একটি প্রতিসারক তল উত্তল ও অপর প্রতিসারক তল অবতল এবং উত্তল পৃষ্ঠের বক্রতা ব্যাসার্ধ অবতল পৃষ্ঠের তুলনায় কম তাকে অবতলোত্তল লেন্স বলা হয়।

5.43 (a), (b) ও (c) নং চিত্রে যথাক্রমে উভোত্তল লেন্স, সমতলোত্তল লেন্স ও অবতলোত্তল লেন্স দেখানো হয়েছে।

প্রতিসারক তল দ্বয়ের আকারের ভিত্তিতে অবতল লেন্স কয় প্রকার ও কী কী? প্রত্যেক প্রকারের চিত্রসহ সংজ্ঞা লেখো।

প্রতিসারক তল দ্বয়ের আকারের ভিত্তিতে অবতল লেন্স তিন ধরনের হতে পারে – উভাবতল লেন্স, সমতলাবতল লেন্স এবং উত্তলাবতল লেন্স।

উভাবতল লেন্স – যে অবতল লেন্সের উভয় প্রতিসারক তলই অবতল তাকে উভাবতল লেন্স বলা হয়।

সমতলাবতল লেন্স – যে অবতল লেন্সের একটি প্রতিসারক তল অবতল ও অপর প্রতিসারক তল সমতল তাকে সমতলাবতল লেন্স বলা হয়।

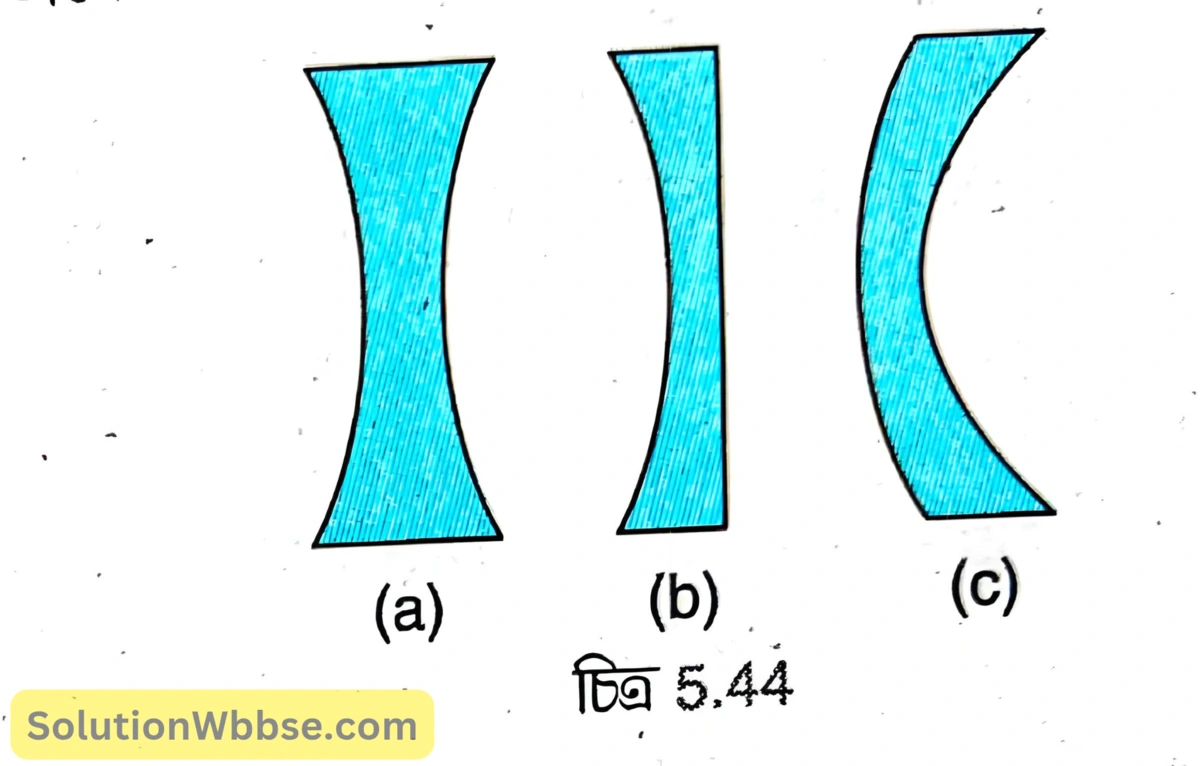
উত্তলাবতল লেন্স – যে অবতল লেন্সের একটি প্রতিসারক তল উত্তল ও অপর প্রতিসারক তল অবতল এবং অবতল পৃষ্ঠের বক্রতা ব্যাসার্ধ উত্তল পৃষ্ঠের তুলনায় কম তাকে উত্তলাবতল লেন্স বলা হয়।

5.44 (a), (b) ও (c) নং চিত্রে যথাক্রমে উভাবতল লেন্স, সমতলাবতল লেন্স ও উত্তলাবতল লেন্স দেখানো হয়েছে।

সমোত্তল ও সমাবতল লেন্স কাকে বলে?

সমোত্তল লেন্স – যে উভোত্তল লেন্সের উভয় প্রতিসারক তলের বক্রতা ব্যাসার্ধ সমান তাকে সমোত্তল লেন্স বলা হয়।

সমাবতল লেন্স – যে উভাবতল লেন্সের উভয় প্রতিসারক তলের বক্রতা ব্যাসার্ধ সমান তাকে সমাবতল লেন্স বলা হয়।

সমতলোত্তল ও সমতলাবতল লেন্সের আলোককেন্দ্রটির চিত্রটি আঁকো?

সমতলোত্তল ও সমতলাবতল লেন্সের আলোককেন্দ্র প্রধান অক্ষ ও গোলীয় তলের ছেদবিন্দুতে অবস্থিত। 5.45 (a) ও (b) নং চিত্রে যথাক্রমে সমতলোত্তল ও সমতলাবতল লেন্সের \( O \) হল আলোককেন্দ্র।

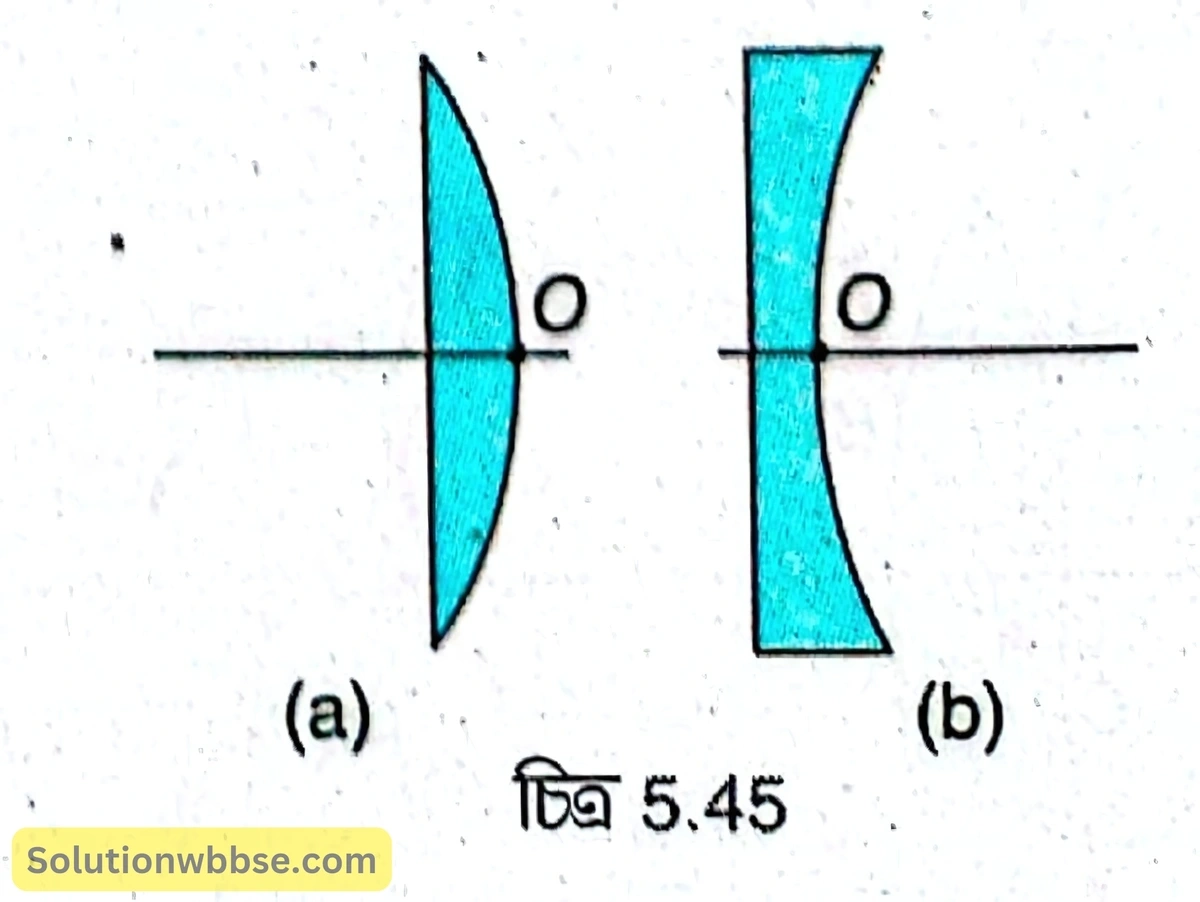
অবতলোত্তল ও উত্তলাবতল লেন্সের আলোককেন্দ্রটির চিত্রটি আঁকো?

অবতলোত্তল ও উত্তলাবতল লেন্সের আলোককেন্দ্র লেন্সের বাইরে, প্রধান অক্ষের ওপর, গোলীয় পৃষ্ঠের কাছে অবস্থিত। 5.46 (a) ও (b) নং চিত্রে যথাক্রমে অবতলোত্তল ও উত্তলাবতল লেন্সের \( O \) হল আলোককেন্দ্র।

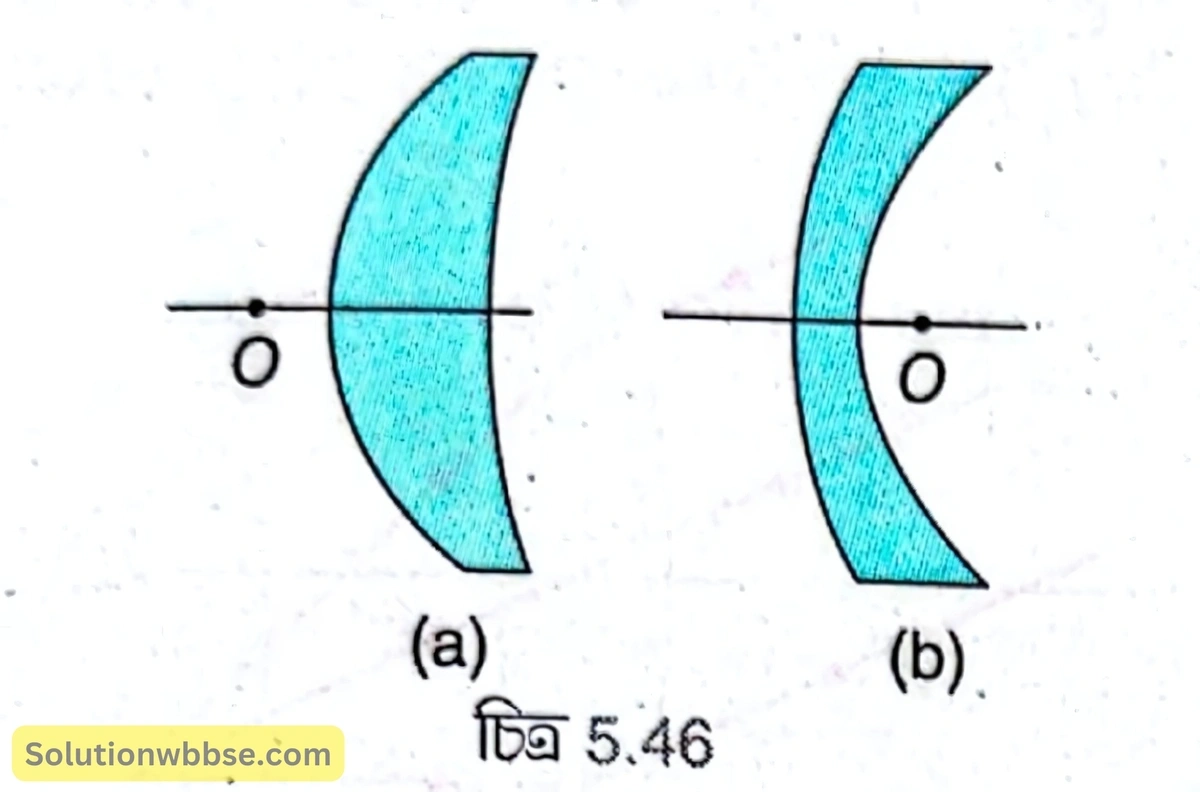
উত্তল লেন্সের অভিসারী ক্রিয়া ব্যাখ্যা করো।

মনে করি, উত্তল লেন্সের প্রধান অক্ষের সমান্তরাল রশ্মিগুচ্ছ লেন্সের ওপর আপতিত হল [চিত্র 5.47]। উত্তল লেন্সে এই সমান্তরাল রশ্মিগুচ্ছের প্রতিসরণ কেমন হবে তা জানার জন্য লেন্সকে অসংখ্য ছোটো ছোটো প্রিজমের সমষ্টি হিসেবে ধরা হল। প্রধান অক্ষের ওপরের ও নীচের প্রিজমগুলির ভূমি প্রধান অক্ষের দিকে। তাই প্রধান অক্ষের সমান্তরালভাবে আপতিত রশ্মি যে-কোনো ছোটো প্রিজমের ওপর আপতিত হলে প্রতিসরণের পর প্রিজমের ভূমির দিকে বেঁকে যায়। ফলে সমান্তরাল রশ্মিগুচ্ছ প্রতিসরণের পর প্রধান অক্ষের ওপর একটি নির্দিষ্ট বিন্দুতে মিলিত হয়, অর্থাৎ উত্তল লেন্স সমান্তরাল রশ্মিগুচ্ছকে অভিসারী রশ্মিগুচ্ছে পরিণত করে। এইজন্য উত্তল লেন্সকে অভিসারী লেন্স বলা হয়।

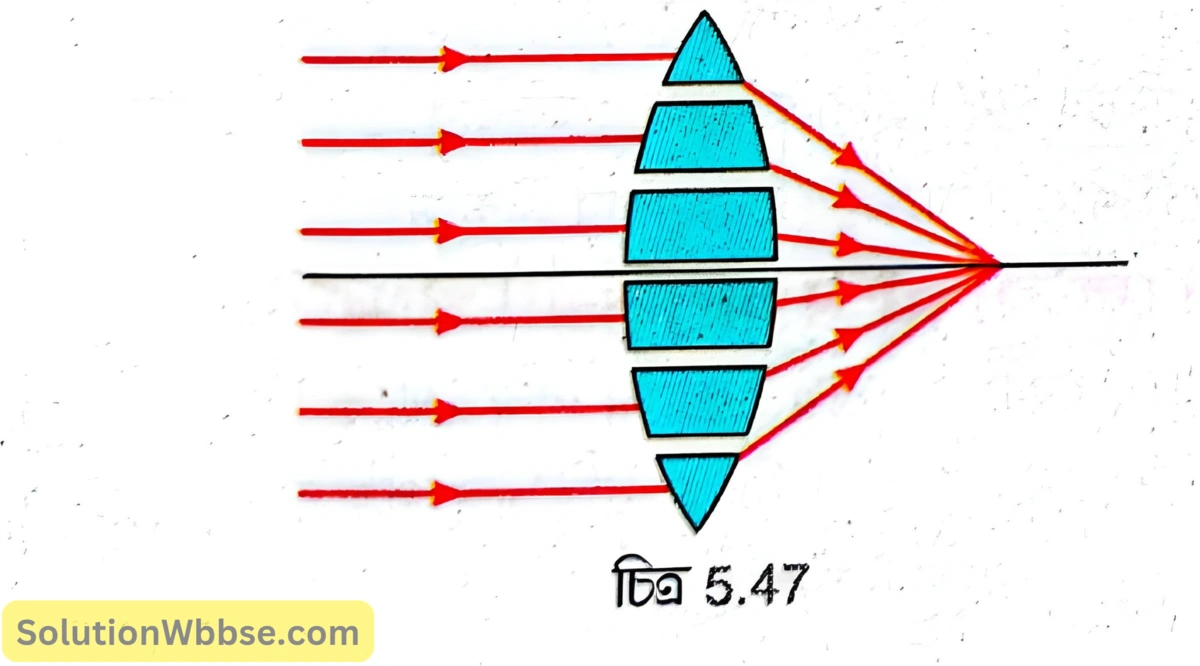
অবতল লেন্সের অপসারী ক্রিয়া ব্যাখ্যা করো।

মনে করি, অবতল লেন্সের প্রধান অক্ষের সমান্তরাল রশ্মিগুচ্ছ লেন্সের ওপর আপতিত হল [চিত্র 5.48]। অবতল লেন্সে এই সমান্তরাল রশ্মিগুচ্ছের প্রতিসরণ কেমন হবে তা জানার জন্য লেন্সকে অসংখ্য ছোটো ছোটো প্রিজমের সমষ্টি হিসেবে ধরা হল। প্রধান অক্ষের ওপর ও নীচের প্রিজমগুলির ভূমি অবতল লেন্সের প্রান্তের দিকে হয়। তাই প্রধান অক্ষের সমান্তরালভাবে আপতিত রশ্মি যে-কোনো ছোটো প্রিজমের ওপর আপতিত হলে প্রতিসরণের পর ভূমির দিকে অর্থাৎ অবতল লেন্সের প্রান্তের দিকে বেঁকে যায়। ফলে সমান্তরাল রশ্মিগুচ্ছ প্রতিসরণের পর প্রধান অক্ষের ওপর একটি নির্দিষ্ট বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়, অর্থাৎ অবতল লেন্স সমান্তরাল রশ্মিগুচ্ছকে অপসারি রশ্মিগুচ্ছে পরিণত করে। এইজন্য অবতল লেন্সকে অপসারী লেন্স বলা হয়।

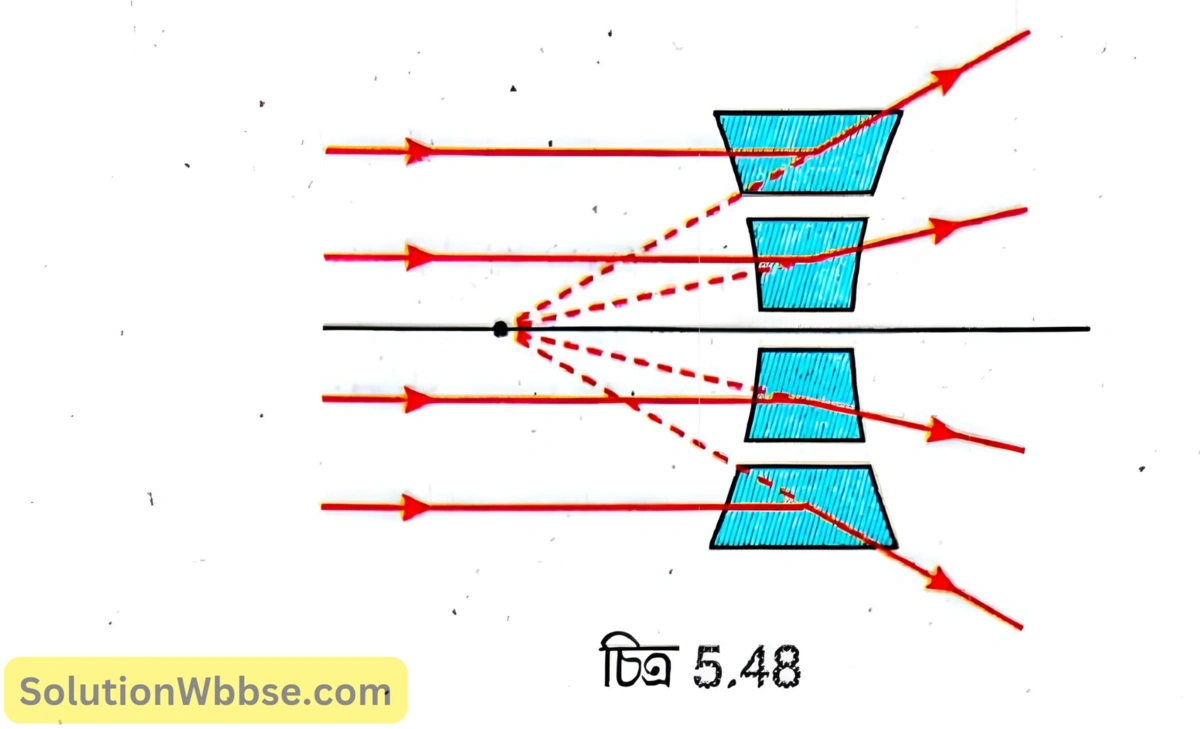
চিত্রসহ সংজ্ঞা লেখো – উত্তল লেন্সের মুখ্য ফোকাস (বা দ্বিতীয় মুখ্য ফোকাস), ফোকাস দূরত্ব, ফোকাস তল।

মুখ্য ফোকাস (বা দ্বিতীয় মুখ্য ফোকাস) – উত্তল লেন্সের প্রধান অক্ষের সমান্তরালভাবে আপতিত সমান্তরাল রশ্মিগুচ্ছ লেন্স দ্বারা প্রতিসরণের পর প্রধান অক্ষের ওপর একটি বিন্দুতে মিলিত হয়। এই বিন্দুকে উত্তল লেন্সের মুখ্য ফোকাস (বা দ্বিতীয় মুখ্য ফোকাস) বলা হয়। 5.49 নং চিত্রে \( F \) হল উত্তল লেন্সের মুখ্য ফোকাস (বা দ্বিতীয় মুখ্য ফোকাস, এটিকে \( F_2 \) দিয়েও লেখা হয়)।

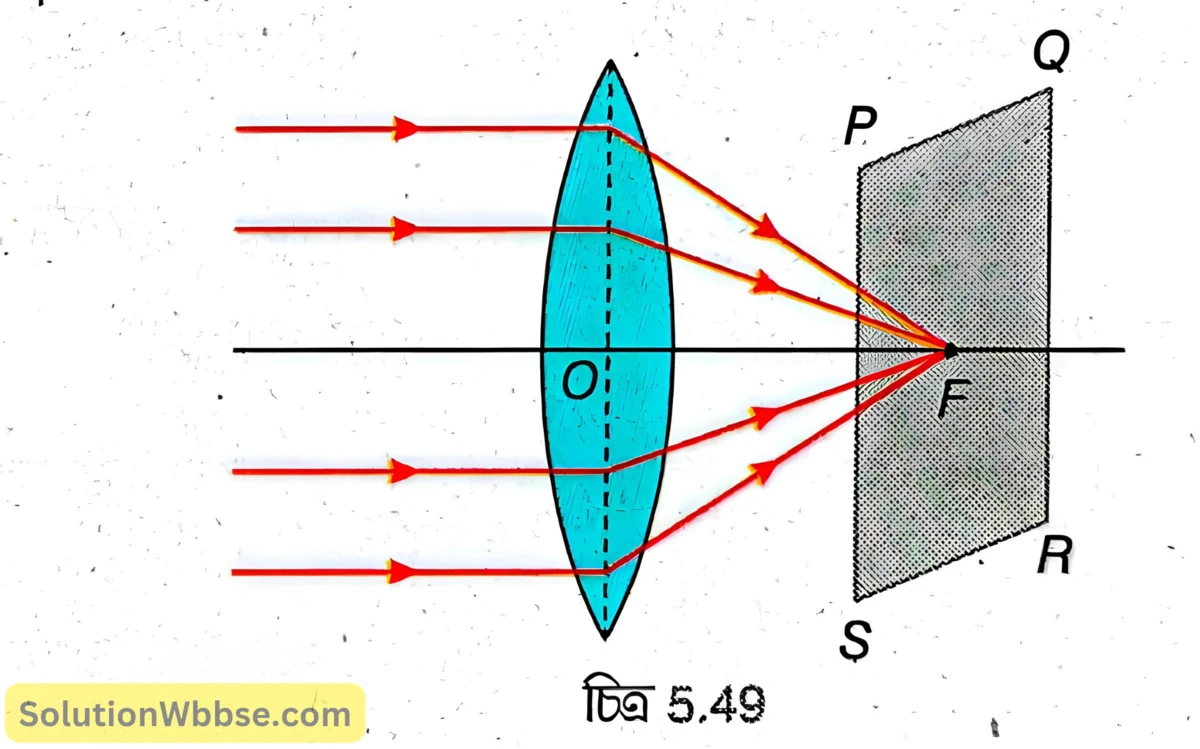
ফোকাস দূরত্ব – কোনো লেন্সের আলোককেন্দ্র থেকে মুখ্য ফোকাসের দূরত্বকে ফোকাস দূরত্ব বলা হয়। 5.49 নং চিত্রে \( OF \) হল উত্তল লেন্সের ফোকাস দূরত্ব।

ফোকাস তল – লেন্সের প্রধান অক্ষের সঙ্গে লম্ব ও মুখ্য ফোকাসগামী কাল্পনিক সমতলকে ফোকাস তল বলা হয়। 5.49 নং চিত্রে \( PQRS \) হল উত্তল লেন্সের ফোকাস তল।

উত্তল লেন্স অপসারী লেন্সের ন্যায় এবং অবতল লেন্স অভিসারী লেন্সের ন্যায় আচরণ করার কারণ উদাহরণসহ লেখো।

কোনো লেন্সের উপাদানের প্রতিসরাঙ্ক পারিপার্শ্বিক মাধ্যমের প্রতিসরাঙ্কের চেয়ে কম হলে উত্তল লেন্স অপসারী লেন্সের ন্যায় এবং অবতল লেন্স অভিসারী লেন্সের ন্যায় আচরণ করে। যেমন কাচ \( \left(\mu_g=1.5\right) \) নির্মিত কোনো উত্তল লেন্সকে কার্বন ডাইসালফাইডে \( \left(\mu_c=1.63\right) \) নিমজ্জিত করলে অপসারী লেন্সের ন্যায় আচরণ করে এবং বায়ুর \( \left(\mu\approx1\right) \) বুদবুদ জলের \( \left(\mu_w=1.33\right) \) মধ্যে অপসারী লেন্সের ন্যায় আচরণ করে।

অবতল লেন্সের মুখ্য ফোকাসের (বা দ্বিতীয় মুখ্য ফোকাসের) চিত্রসহ সংজ্ঞা লেখো। চিত্রে ফোকাস দূরত্ব ও ফোকাস তল চিহ্নিত করো।

অবতল লেন্সের প্রধান অক্ষের সমান্তরালভাবে আপতিত সমান্তরাল রশ্মিগুচ্ছ লেন্স দ্বারা প্রতিসরণের পর প্রধান অক্ষের ওপর একটি বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়। এই বিন্দুকে অবতল লেন্সের মুখ্য ফোকাস (বা দ্বিতীয় মুখ্য ফোকাস) বলা হয়।

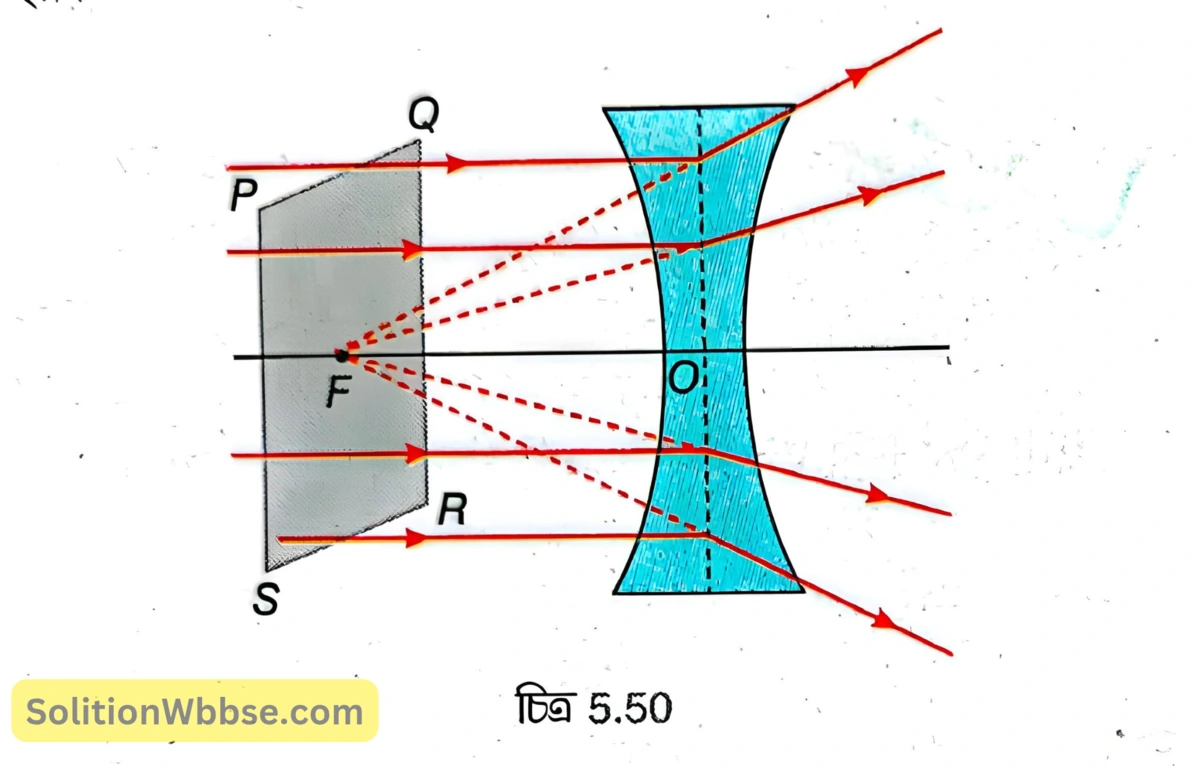
5.50 নং চিত্রে \( F \) হল অবতল লেন্সের মুখ্য ফোকাস (বা দ্বিতীয় মুখ্য ফোকাস, এটিকে \( F_2 \) দিয়েও লেখা হয়)। \( OF \) হল অবতল লেন্সের ফোকাস দূরত্ব এবং \( PQRS \) হল ফোকাস তল।

চিত্রসহ সংজ্ঞা লেখো – উত্তল ও অবতল লেন্সের, প্রথম মুখ্য ফোকাস।

উত্তল লেন্সের প্রথম মুখ্য ফোকাস – কোনো উত্তল লেন্সের প্রধান অক্ষের ওপর অবস্থিত কোনো বিন্দু থেকে আগত অপসারী আলোকরশ্মিগুচ্ছ লেন্স দ্বারা প্রতিসরণের পর প্রধান অক্ষের সমান্তরালভাবে নির্গত হলে ওই বিন্দুকে উত্তল লেন্সের প্রথম মুখ্য ফোকাস বলে। 5.51 (a) নং চিত্রে \( F_1 \) হল উত্তল লেন্সের প্রথম মুখ্য ফোকাস।

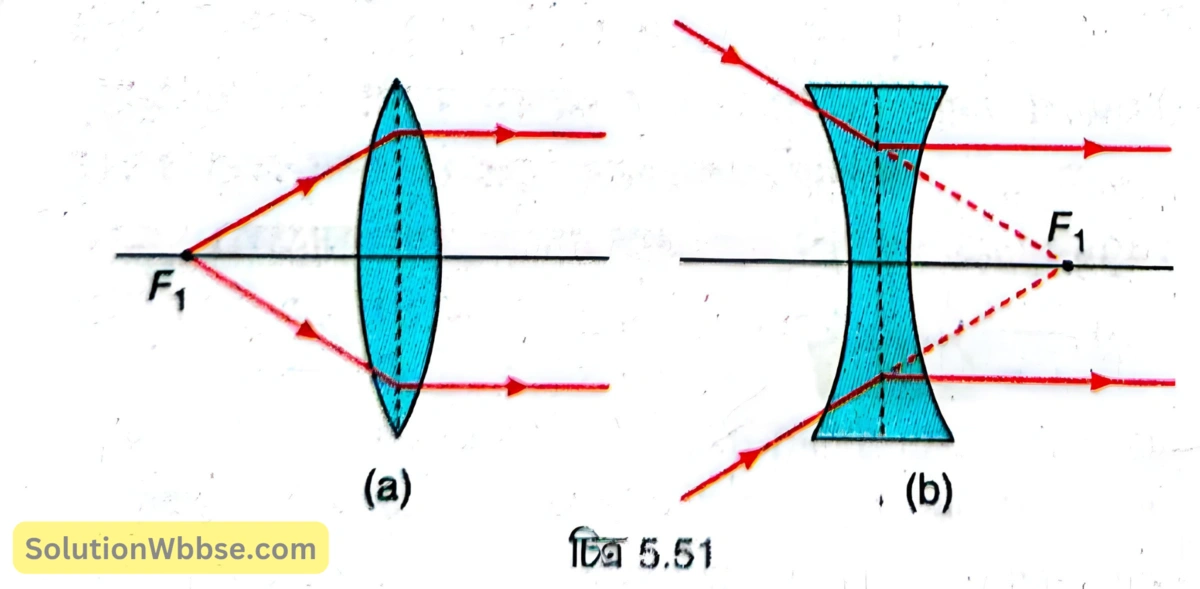
অবতল লেন্সের প্রথম মুখ্য ফোকাস – কোনো অবতল লেন্সের প্রধান অক্ষের ওপর অবস্থিত একটি বিন্দুর দিকে পরিচালিত অভিসারী রশ্মিগুচ্ছ লেন্সের ওপর আপতিত হয়ে লেন্স দ্বারা প্রতিসরণের পর প্রধান অক্ষের সমান্তরালভাবে নির্গত হলে ওই বিন্দুকে অবতল লেন্সের প্রথম মুখ্য ফোকাস বলা হয়। 5.51 (b) নং চিত্রে \( F_1 \) হল অবতল লেন্সের প্রথম মুখ্য ফোকাস।

উত্তল লেন্সের গৌণ ফোকাস কাকে বলে?

উত্তল লেন্সের গৌণ ফোকাস – উত্তল লেন্সের প্রধান অক্ষের সঙ্গে আনতভাবে সমান্তরাল রশ্মিগুচ্ছ লেন্সের ওপর আপতিত হয়ে প্রতিসরণের পর ফোকাস তলের ওপর একটি বিন্দুতে মিলিত হলে ওই বিন্দুকে গৌণ ফোকাস বলা হয়। 5.52 নং চিত্রে \( F’ \) হল উত্তল লেন্সের গৌণ ফোকাস।

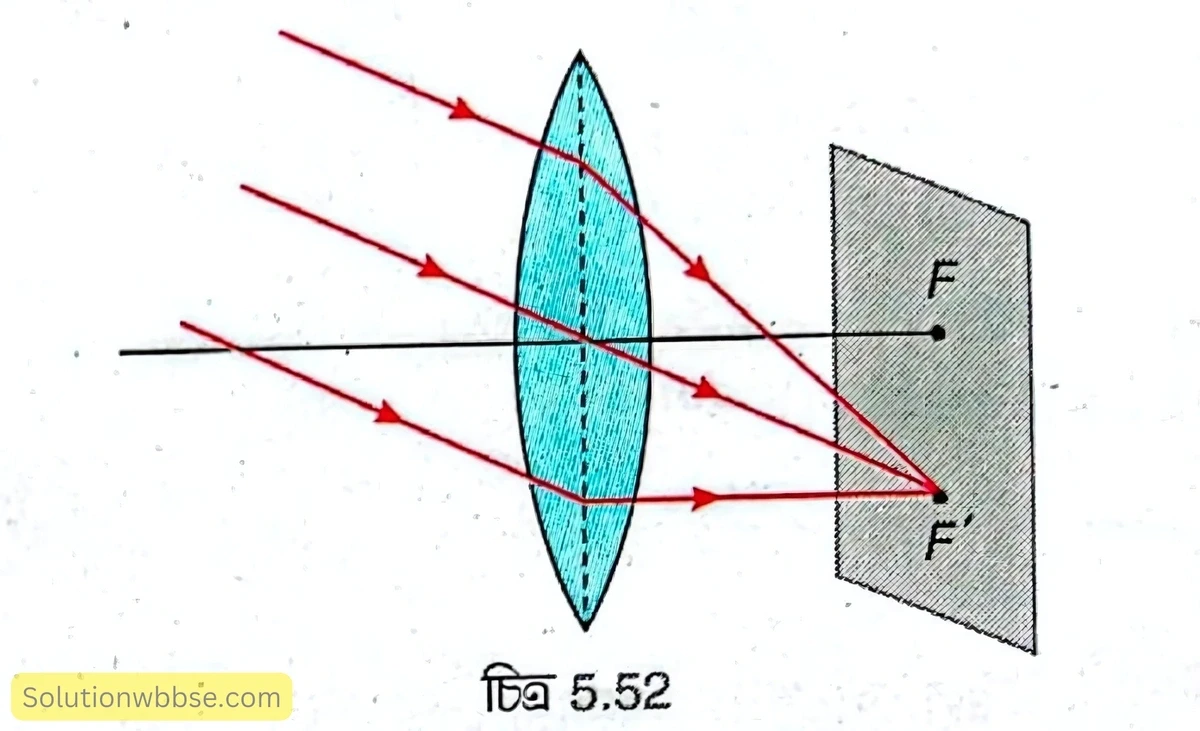
অবতল লেন্সের গৌণ ফোকাস কাকে বলে?

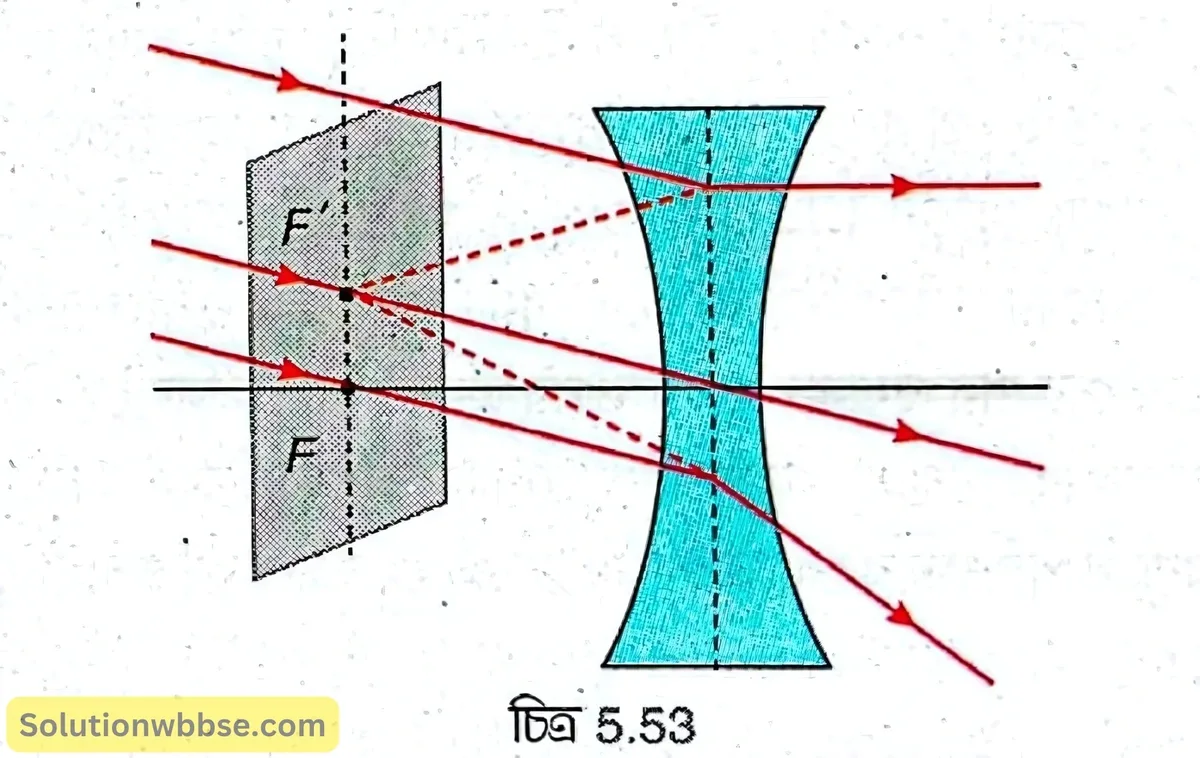
অবতল লেন্সের গৌণ ফোকাস – অবতল লেন্সের প্রধান অক্ষের সঙ্গে আনতভাবে সমান্তরাল রশ্মিগুচ্ছ লেন্সের ওপর আপতিত হয়ে প্রতিসরণের পর ফোকাস তলের ওপর কোনো বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হলে ওই বিন্দুকে গৌণ ফোকাস বলা হয়।

5.53 নং চিত্রে \( F’ \) হল অবতল লেন্সের গৌণ ফোকাস। লেন্সের গৌণ ফোকাস কোনো স্থির বিন্দু নয়।

পাতলা লেন্সে রশ্মি অনুসরণ পদ্ধতিটি লিখ?

পাতলা লেন্সে রশ্মি অনুসরণ পদ্ধতি – লেন্সের সামনে থাকা কোনো বস্তুর কোনো বিন্দু থেকে বিভিন্ন দিকে অসংখ্য রশ্মি নির্গত হয়। কিন্তু প্রতিবিম্ব গঠনের জন্য যে-কোনো বিন্দু থেকে দুটি নির্গত রশ্মি নেওয়া হয়।

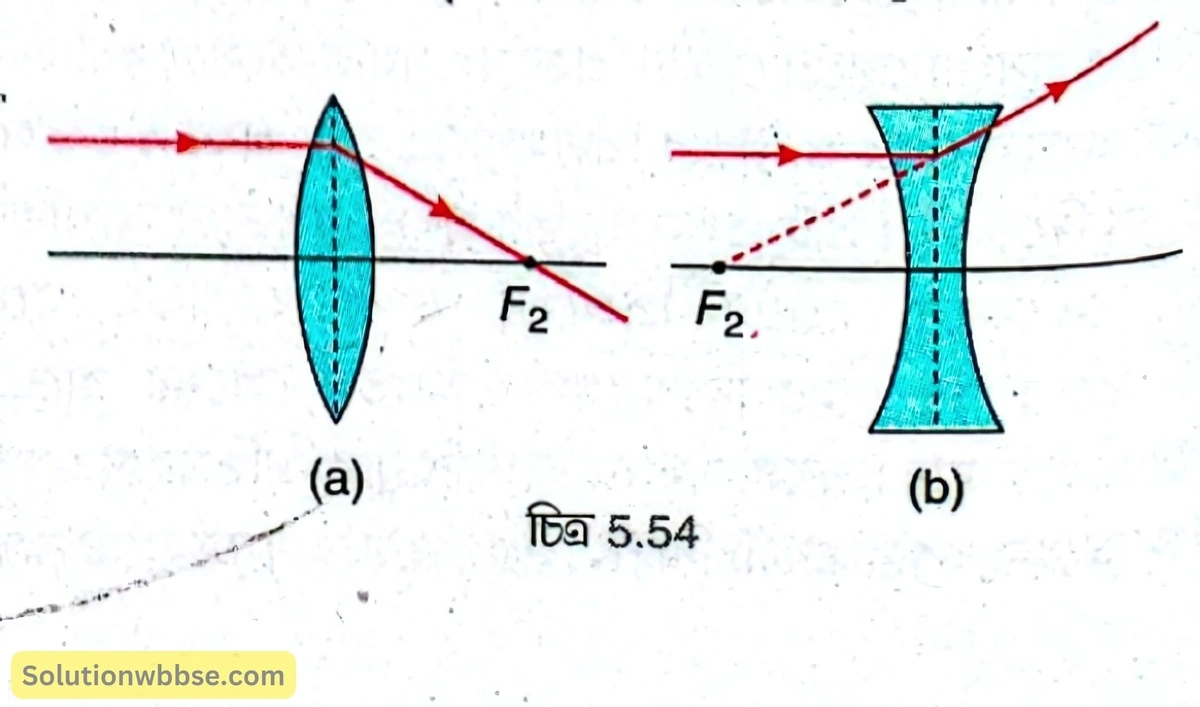
(1) লেন্সের প্রধান অক্ষের সমান্তরাল রশ্মি, লেন্স দ্বারা প্রতিসরণের পর উত্তল লেন্সের ক্ষেত্রে মুখ্য ফোকাসের (বা দ্বিতীয় মুখ্য ফোকাস) মধ্য দিয়ে যায় [চিত্র 5.54 (a)] ও অবতল লেন্সের ক্ষেত্রে মুখ্য ফোকাস (বা দ্বিতীয় মুখ্য ফোকাস) থেকে অপসৃত হচ্ছে বলে মনে হয় [চিত্র 5.54 (b)]।

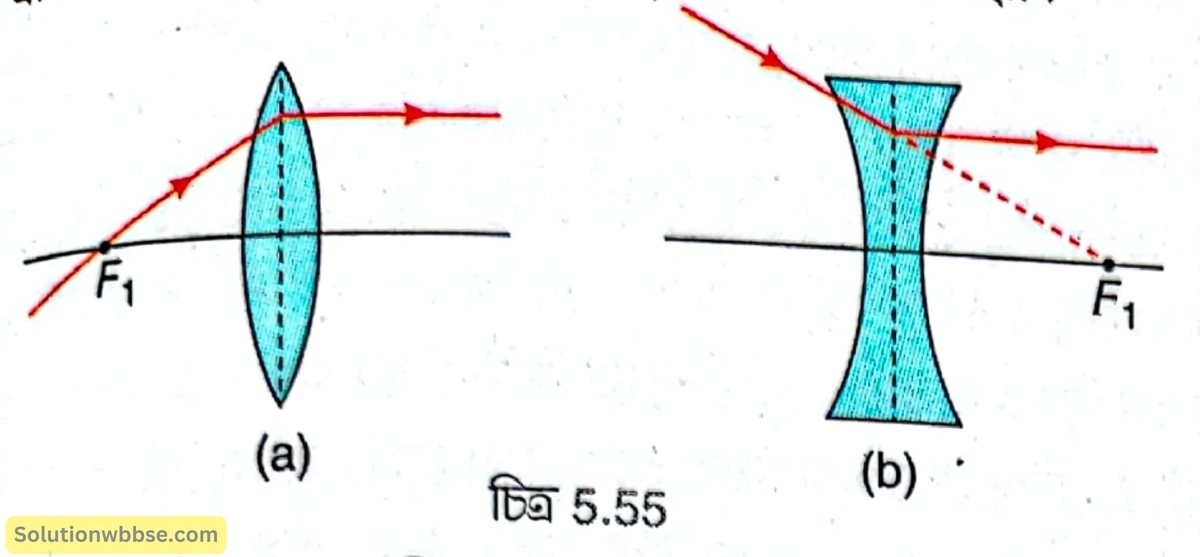
(2) উত্তল লেন্সের প্রথম মুখ্য ফোকাসগামী কোনো রশ্মি [চিত্র 5.55 (a)] এবং অবতল লেন্সের প্রথম মুখ্য ফোকাসের দিকে পরিচালিত কোনো রশ্মি [চিত্র 5.55 (b)] লেন্স দ্বারা প্রতিসরণের পর প্রধান অক্ষের সমান্তরালে নির্গত হয়।

(3) উত্তল লেন্স [চিত্র 5.56 (a)] ও অবতল লেন্সের [চিত্র 5.56 (b)] আলোককেন্দ্রের মধ্য দিয়ে যে রশ্মি যায়, সেই রশ্মি সোজা পথে লেন্সের মধ্য দিয়ে চলে যায়।

উত্তল লেন্স দ্বারা কোনো বস্তুর অবশীর্ষ, খর্বকায় সদবিম্ব গঠন চিত্রসহ ব্যাখ্যা করো।

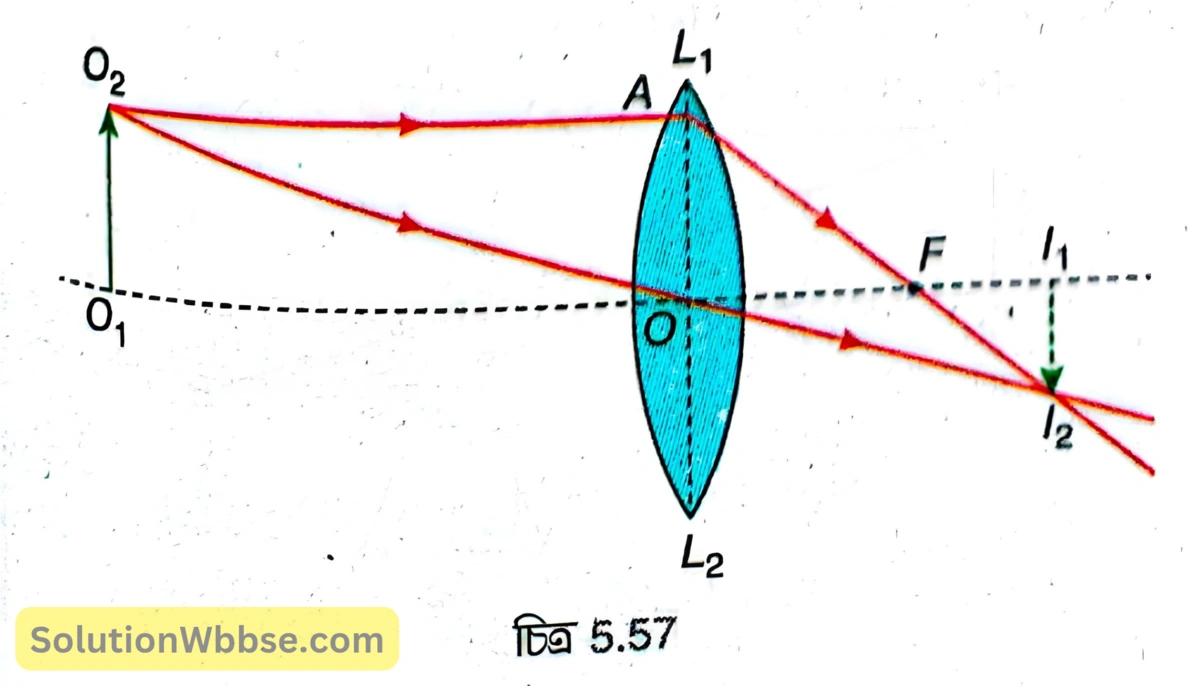
উত্তল লেন্স দ্বারা কোনো বস্তুর অবশীর্ষ, খর্বকায় সদবিম্ব পেতে গেলে বস্তুকে ফোকাস দূরত্বের দ্বিগুণ বা \( 2f \) অপেক্ষা বেশি দূরত্বে রাখতে হবে। 5.57 নং চিত্রে \( L_1L_2 \) ক্ষুদ্র উন্মেষযুক্ত একটি পাতলা উত্তল লেন্স। লেন্সের প্রধান অক্ষের ওপর লম্বভাবে \( 2f \) অপেক্ষা বেশি দূরত্বে অবস্থিত \( O_1O_2 \) একটি বিস্তৃত বস্তু। \( O_2 \) থেকে আগত প্রধান অক্ষের সমান্তরাল \( O_2A \) রশ্মি লেন্স দ্বারা প্রতিসরণের পর মুখ্য ফোকাস \( F \) -এর মধ্য দিয়ে যায়। অপর একটি রশ্মি \( O_2O \) লেন্সের আলোককেন্দ্রের মধ্য দিয়ে গিয়ে কোনোরকম চ্যুতি ছাড়াই সোজা চলে যায়। প্রতিসৃত রশ্মি দুটি পরস্পরকে \( I_2 \) বিন্দুতে ছেদ করে। \( I_2 \) থেকে প্রধান অক্ষের ওপর \( I_2I_1 \) লম্ব টানা হল। \( I_2I_1 \) হল \( O_1O_2 \) বস্তুর সদবিম্ব। এখানে প্রতিবিম্বের সাইজ বস্তুর তুলনায় ছোটো তাই প্রতিবিম্ব খর্বকায় এবং প্রতিবিম্ব বস্তু সাপেক্ষে উলটো তাই প্রতিবিম্ব অবশীর্ষ অর্থাৎ প্রতিবিম্ব সৎ, অবশীর্ষ ও খর্বকায়।

উত্তল লেন্স দ্বারা কোনো বস্তুর অবশীর্ষ, সমান সাইজের সদবিম্ব গঠন চিত্রসহ ব্যাখ্যা করো।

উত্তল লেন্স দ্বারা কোনো বস্তুর অবশীর্ষ, সমান সাইজের সদবিম্ব পেতে গেলে বস্তুকে ফোকাস দূরত্বের দ্বিগুণ বা \( 2f \) দূরত্বে রাখতে হবে। 5.58 নং চিত্রে \( L_1L_2 \) ক্ষুদ্র উন্মেষযুক্ত একটি পাতলা উত্তল লেন্স। লেন্সের প্রধান অক্ষের ওপর লম্বভাবে \( 2f \) দূরত্বে অবস্থিত \( O_1O_2 \) একটি বিস্তৃত বস্তু। \( O_2 \) থেকে আগত প্রধান অক্ষের সমান্তরাল \( O_2A \) রশ্মি লেন্স দ্বারা প্রতিসরণের পর মুখ্য ফোকাস \( F \) -এর মধ্য দিয়ে যায়। অপর একটি রশ্মি \( O_2O \) লেন্সের আলোককেন্দ্রের মধ্য দিয়ে গিয়ে কোনোরকম চ্যুতি ছাড়াই সোজা চলে যায়। প্রতিসৃত রশ্মি দুটি পরস্পরকে \( I_2 \) বিন্দুতে ছেদ করে। \( I_2 \) থেকে প্রধান অক্ষের ওপর \( I_2I_1 \) লম্ব টানা হল। \( I_1I_2 \) হল \( O_1O_2 \) বস্তুর সদবিম্ব। এখানে প্রতিবিম্বের সাইজ বস্তুর সমান সাইজের এবং প্রতিবিম্ব বস্তু সাপেক্ষে উলটো তাই প্রতিবিম্ব অবশীর্ষ অর্থাৎ প্রতিবিম্ব সৎ, অবশীর্ষ ও সমান সাইজের।

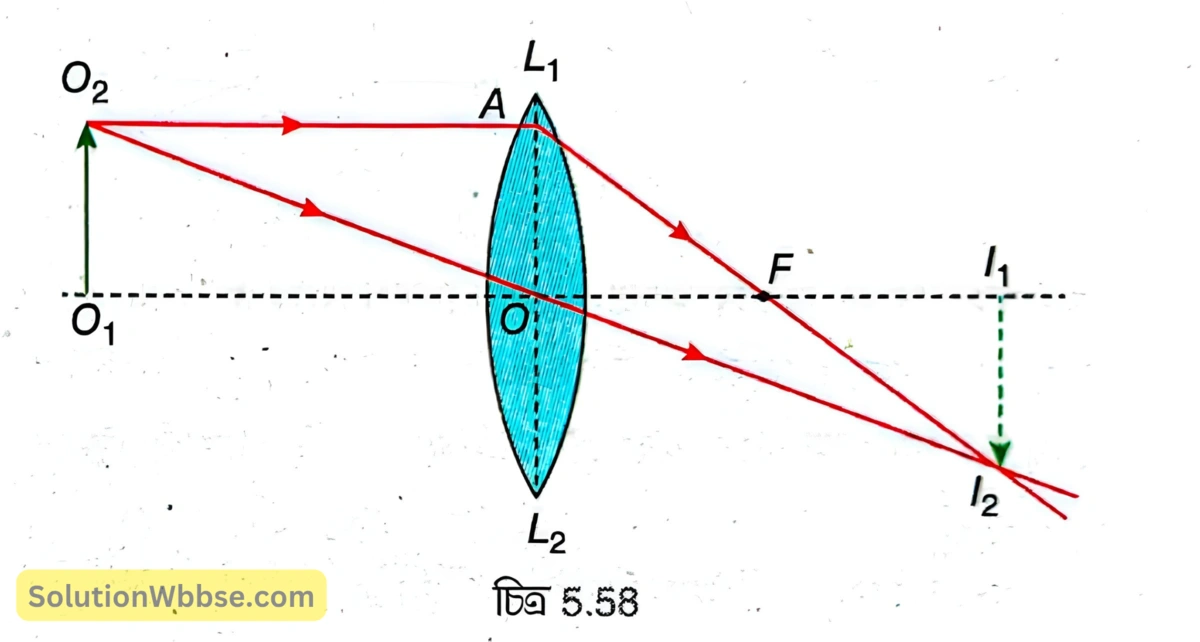
উত্তল লেন্স দ্বারা কোনো বস্তুর অবশীর্ষ, বিবর্ধিত সদবিম্ব গঠন চিত্রসহ ব্যাখ্যা করো।

উত্তল লেন্স দ্বারা কোনো বস্তুর অবশীর্ষ, বিবর্ধিত সদবিম্ব পেতে গেলে বস্তুকে ফোকাস দূরত্ব বা \( f \) -এর বেশি দূরত্বে কিন্তু দ্বিগুণ ফোকাস দূরত্ব বা \( 2f \) -এর কম দূরত্বে রাখতে হবে। 5.59 নং চিত্রে \( L_1L_2 \) ক্ষুদ্র উন্মেষযুক্ত একটি পাতলা উত্তল লেন্স। লেন্সের প্রধান অক্ষের ওপর লম্বভাবে অবস্থিত \( O_1O_2 \) একটি বিস্তৃত বস্তু যা \( f \) -এর বেশি কিন্তু \( 2f \) -এর কম দূরত্বে অবস্থিত। \( O_2 \) থেকে আগত প্রধান অক্ষের সমান্তরাল \( O_2A \) রশ্মি লেন্স দ্বারা প্রতিসরণের পর মুখ্য ফোকাস \( F \) -এর মধ্য দিয়ে যায়। অপর একটি রশ্মি \( O_2O \) লেন্সের আলোককেন্দ্রের মধ্য দিয়ে গিয়ে কোনোরকম চ্যুতি ছাড়াই সোজা চলে যায়। প্রতিসৃত রশ্মি দুটি পরস্পরকে \( I_2 \) বিন্দুতে ছেদ করে। \( I_2 \) থেকে প্রধান অক্ষের ওপর \( I_2I_1 \) লম্ব টানা হল। \( I_1I_2 \) হল \( O_1O_2 \) বস্তুর সদবিম্ব। এখানে প্রতিবিম্বের সাইজ বস্তুর তুলনায় বড়ো তাই প্রতিবিম্ব বিবর্ধিত এবং প্রতিবিম্ব বস্তু সাপেক্ষে উলটো তাই প্রতিবিম্ব অবশীর্ষ অর্থাৎ প্রতিবিম্ব সৎ, অবশীর্ষ ও বিবর্ধিত।

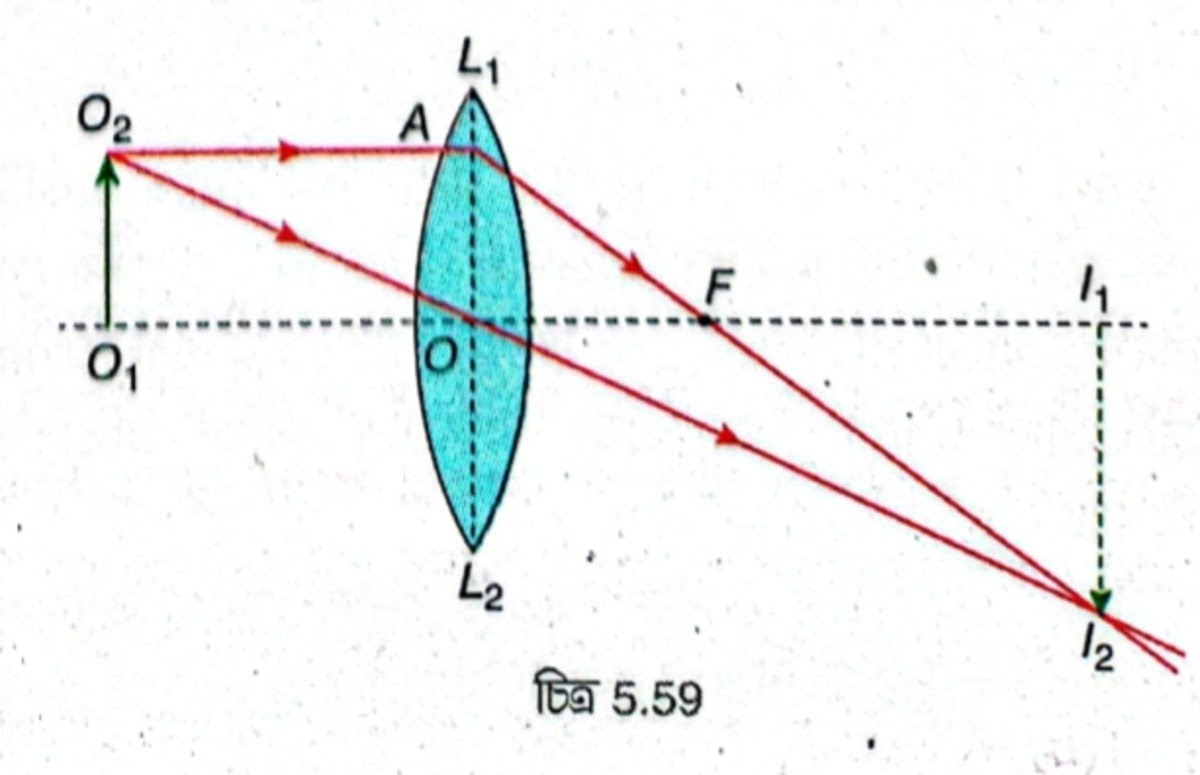
উত্তল লেন্স দ্বারা কোনো বস্তুর সমশীর্ষ, বিবর্ধিত অসদবিম্ব গঠন চিত্রসহ ব্যাখ্যা করো।

উত্তল লেন্স দ্বারা কোনো বস্তুর সমশীর্ষ, বিবর্ধিত অসদবিম্ব পেতে গেলে বস্তুকে ফোকাস দূরত্ব বা \( f \) -এর কম দূরত্বে রাখতে হবে।

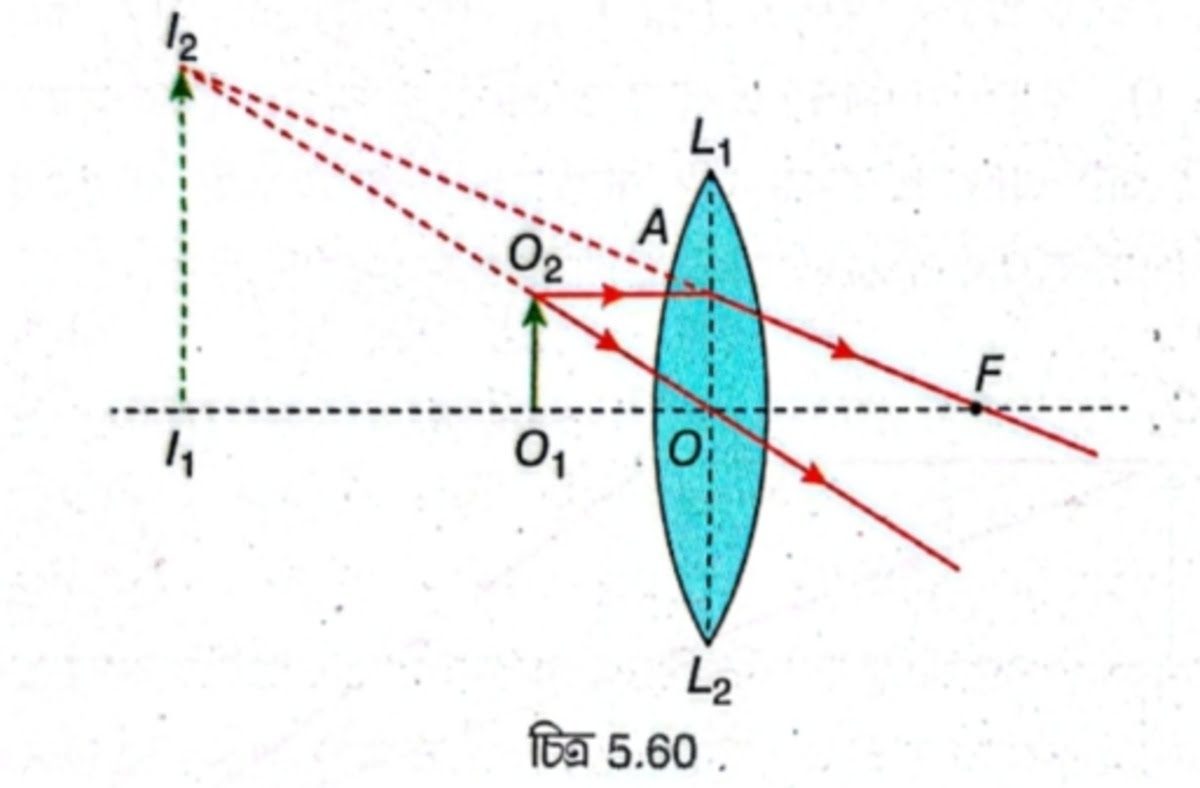
5.60 নং চিত্রে \( L_1L_2 \) ক্ষুদ্র উন্মেষযুক্ত একটি পাতলা উত্তল লেন্স। লেন্সের প্রধান অক্ষের ওপর লম্বভাবে অবস্থিত \( O_1O_2 \) একটি বিস্তৃত বস্তু যা ফোকাস দূরত্বের চেয়ে কম দূরত্বে আছে। \( O_2 \) থেকে আগত প্রধান অক্ষের সমান্তরাল \( O_2A \) রশ্মি লেন্স দ্বারা প্রতিসরণের পর মুখ্য ফোকাস \( F \) -এর মধ্য দিয়ে যায়। অপর একটি রশ্মি \( O_2O \) লেন্সের আলোককেন্দ্রের মধ্য দিয়ে গিয়ে কোনোরকম চ্যুতি ছাড়াই সোজা চলে যায়। প্রতিসৃত রশ্মি দুটি অপসারী হওয়ায় প্রতিসরণের পর মিলিত হয় না। রশ্মি দুটিকে পিছন দিকে বাড়ালে \( I_2 \) বিন্দুতে মিলিত হয় অর্থাৎ প্রতিসৃত রশ্মি দুটি \( I_2 \) বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়। \( I_2 \) থেকে প্রধান অক্ষের ওপর \( I_2I_1 \) লম্ব টানা হল। \( I_1I_2 \) হল \( O_1O_2 \) বস্তুর অসদবিম্ব। এখানে প্রতিবিম্বের সাইজ বস্তুর চেয়ে বড়ো তাই প্রতিবিম্ব বিবর্ধিত এবং প্রতিবিম্ব বস্তু সাপেক্ষে সোজা অর্থাৎ প্রতিবিম্ব সমশীর্ষ।

বিবর্ধক কাচ হিসেবে উত্তল লেন্সের ব্যবহার চিত্রসহ ব্যাখ্যা করো।

উত্তল লেন্সের ফোকাস দূরত্বের চেয়ে কম দুরত্বে একটি বস্তু রাখলে সমশীর্ষ, বিবর্ধিত অসদবিম্ব গঠিত হয়। লেন্সের যে পার্শ্বে বস্তু থাকে প্রতিবিম্বও সেই দিকেই গঠিত হয় এবং অপর পার্শ্বে চোখ রাখলে বস্তুর বড়ো আকারের সোজা প্রতিবিম্ব দেখা যায়।

কার্যনীতি – এই উত্তল লেন্সকে একটি গোল ফ্রেমে আটকে হাতল যুক্ত করলেই বিবর্ধক কাচ তৈরি করা যাবে।

5.60 নং চিত্রে \( L_1L_2 \) ক্ষুদ্র উন্মেষযুক্ত একটি পাতলা উত্তল লেন্স। লেন্সের প্রধান অক্ষের ওপর লম্বভাবে অবস্থিত \( O_1O_2 \) একটি বিস্তৃত বস্তু যা ফোকাস দূরত্বের চেয়ে কম দূরত্বে আছে। \( O_2 \) থেকে আগত প্রধান অক্ষের সমান্তরাল \( O_2A \) রশ্মি লেন্স দ্বারা প্রতিসরণের পর মুখ্য ফোকাস \( F \) -এর মধ্য দিয়ে যায়। অপর একটি রশ্মি \( O_2O \) লেন্সের আলোককেন্দ্রের মধ্য দিয়ে গিয়ে কোনোরকম চ্যুতি ছাড়াই সোজা চলে যায়। প্রতিসৃত রশ্মি দুটি অপসারী হওয়ায় প্রতিসরণের পর মিলিত হয় না। রশ্মি দুটিকে পিছন দিকে বাড়ালে \( I_2 \) বিন্দুতে মিলিত হয় অর্থাৎ প্রতিসৃত রশ্মি দুটি \( I_2 \) বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়। \( I_2 \) থেকে প্রধান অক্ষের ওপর \( I_2I_1 \) লম্ব টানা হল। \( I_1I_2 \) হল \( O_1O_2 \) বস্তুর অসদবিম্ব। এখানে প্রতিবিম্বের সাইজ বস্তুর চেয়ে বড়ো তাই প্রতিবিম্ব বিবর্ধিত এবং প্রতিবিম্ব বস্তু সাপেক্ষে সোজা অর্থাৎ প্রতিবিম্ব সমশীর্ষ।

ব্যবহার – কোনো ওষুধের প্যাকেটের ওপরের বা সিরাপের বোতলের গায়ে ছোটো ছোটো লেখা পড়ার জন্য, যাঁরা ঘড়ি মেরামত করেন তাঁরা ঘড়ির সূক্ষ্ম যন্ত্রপাতি দেখার জন্য, পরীক্ষাগারে সূক্ষপাঠ দেখার জন্য বিবর্ধক কাচ ব্যবহার করা হয়।

অবতল লেন্স দ্বারা কোনো বস্তুর সমশীর্ষ, অসদবিম্ব গঠন ব্যাখ্যা করো।

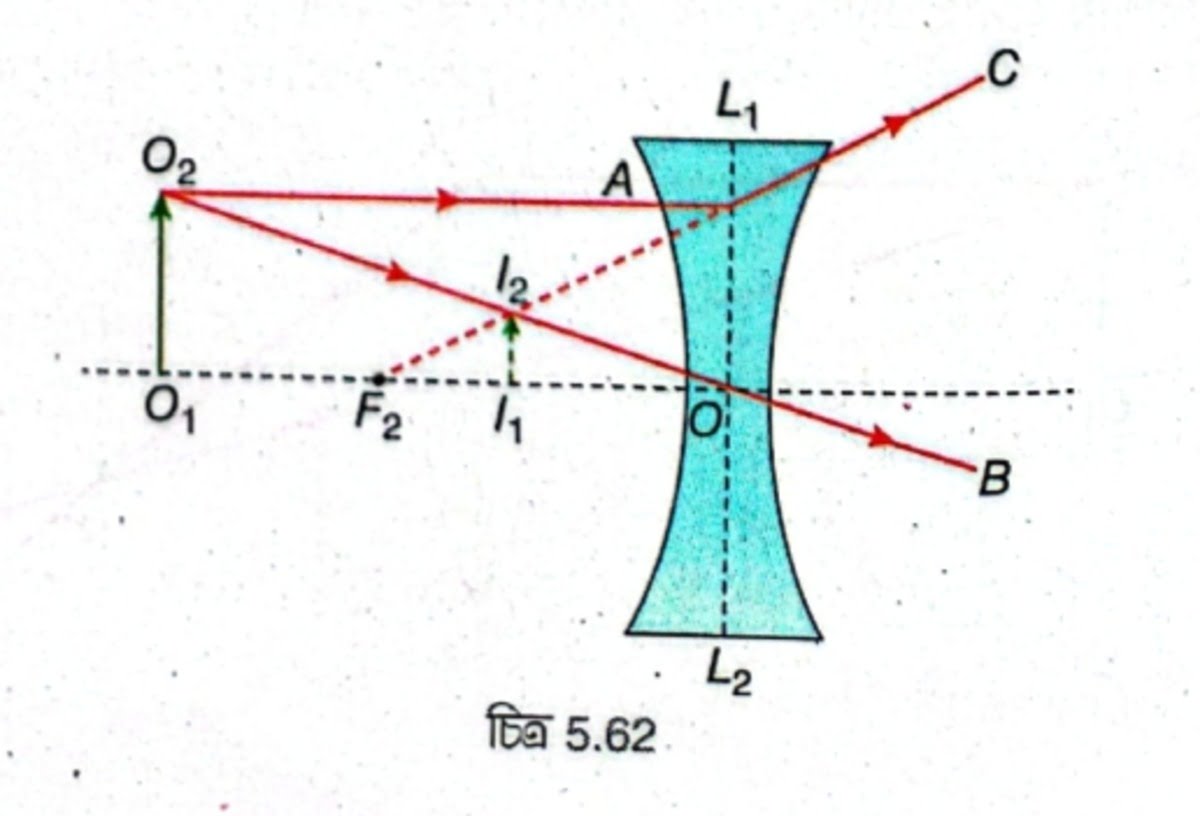
\( L_1L_2 \) হল ক্ষুদ্র উন্মেষযুক্ত একটি পাতলা অবতল লেন্স [চিত্র 5.62]। অবতল লেন্সের প্রধান অক্ষের ওপর লম্বভাবে অবস্থিত \( O_1O_2 \) একটি বিস্তৃত বস্তু। \( O_2 \) থেকে আগত প্রধান অক্ষের সমান্তরাল \( O_2A \) রশ্মি লেন্স দ্বারা প্রতিসরণের পর মুখ্য ফোকাস \( F \) থেকে অপসৃত হচ্ছে বলে মনে হয় এবং \( AC \) পথে যায়। অপর একটি রশ্মি \( O_2O \) লেন্সের আলোককেন্দ্রের মধ্য দিয়ে গিয়ে কোনোরকম চ্যুতি ছাড়াই সোজা চলে যায়। প্রতিসৃত রশ্মি দুটি অপসারী হওয়ায় প্রতিসরণের পর মিলিত হয় না। রশ্মি দুটিকে পিছন দিকে বাড়ালে \( I_2 \) বিন্দুতে মিলিত হয় অর্থাৎ প্রতিসৃত রশ্মি দুটি \( I_2 \) বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়। \( I_2 \) থেকে প্রধান অক্ষের ওপর \( I_2I_1 \) লম্ব টানা হল। \( I_1I_2 \) হল \( O_1O_2 \) বস্তুর অসদবিম্ব। এখানে প্রতিবিম্বের সাইজ বস্তুর তুলনায় ছোটো এবং প্রতিবিম্ব বস্তু সাপেক্ষে সোজা তাই প্রতিবিম্ব অসৎ, খর্বকায় ও সমশীর্ষ।

লেন্সে রৈখিক বিবর্ধন কাকে বলে? উত্তল ও অবতল লেন্সের ক্ষেত্রে রৈখিক বিবর্ধনের রাশিমালাটি প্রতিষ্ঠা করো।

লেন্সে রৈখিক বিবর্ধন – লেন্সের প্রধান অক্ষের ওপর লম্বভাবে অবস্থিত কোনো বস্তুর প্রতিবিম্বের উচ্চতা ও বস্তুর উচ্চতার অনুপাতকে রৈখিক বিবর্ধন বলা হয়।

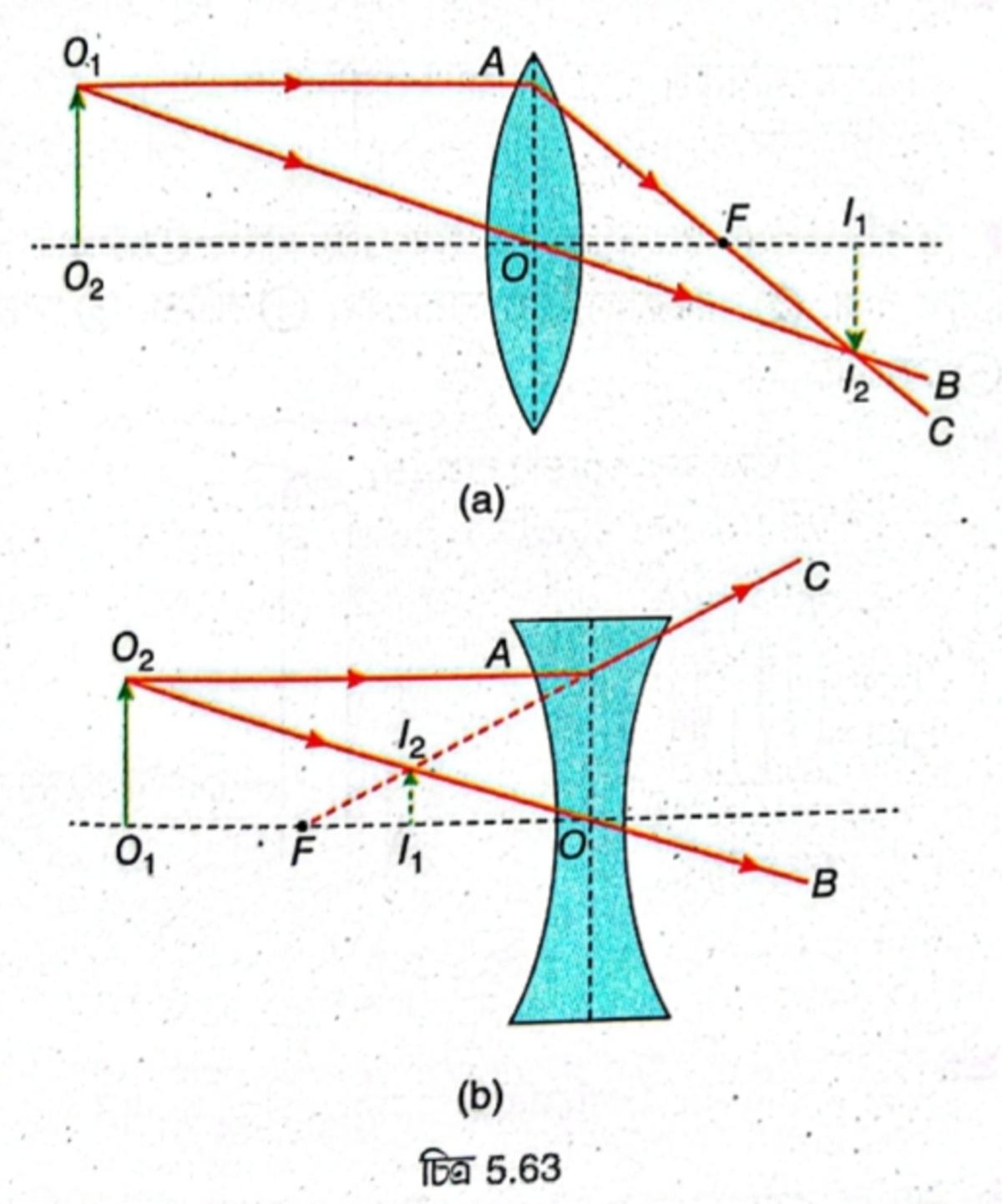
রৈখিক বিবর্ধনের রাশিমালা – 5.63(a) ও (b) নং চিত্রে যথাক্রমে উত্তল লেন্স ও অবতল লেন্সের সামনে প্রধান অক্ষের ওপর লম্বভাবে অবস্থিত \( O_1O_2 \) বিস্তৃত বস্তু ও \( I_1I_2 \) তার প্রতিবিম্ব। বস্তু ও প্রতিবিম্বের উচ্চতা যথাক্রমে \( h_1 \) ও \( h_2 \) হলে, রৈখিক বিবর্ধন, \( m=\frac{h_2}{h_1} \)।

মনে করি, আলোককেন্দ্র \( O \) থেকে বস্তু দূরত্ব, \( OO_1=u \) ও প্রতিবিম্ব দূরত্ব, \( OI_1=v \)

চিত্র থেকে পাই, \( \bigtriangleup OO_1O_2 \) ও \( \bigtriangleup OI_1I_2 \) –এর মধ্যে \( \angle O_1OO_2=\angle I_1OI_2 \) [বিপ্রতীপ কোণ] ও \( \angle OO_1O_2=\angle OI_1I_2 \) [উভয়ই সমকোণ]।

∴ \( \bigtriangleup OO_1O_2 \) ও \( \bigtriangleup OI_1I_2 \) সদৃশ।

∴ \( \frac{O_1O_2}{I_1I_2}=\frac{OO_1}{OI_1} \)

বা, \( \frac{I_1I_2}{O_1O_2}=\frac{OI_1}{OO_1} \)

বা, \( \frac{h_2}{h_1}=\frac vu \)

বা, \( m=\frac vu \)

একটি লেন্স উত্তল না অবতল কীভাবে বুঝবে?

আমরা জানি, উত্তল লেন্স ফোকাস দূরত্বের কম দূরত্বে থাকা কোনো বস্তুর সমশীর্ষ, বিবর্ধিত অসদবিম্ব গঠন করে এবং অবতল লেন্স তার সামনে থাকা কোনো বস্তুর সর্বদা সমশীর্ষ, খর্বকায় অসদবিম্ব গঠন করে। একটি পেনসিলকে কোনো লেন্সের একপাশে কাছে রেখে অপর পাশ থেকে লেন্সের মধ্য দিয়ে দেখলে যদি পেনসিলের বিবর্ধিত, সমশীর্ষ প্রতিবিম্ব দেখা যায় তাহলে বোঝা যাবে লেন্সটি উত্তল কিন্তু যদি প্রতিবিম্বটি খর্বকায়, সমশীর্ষ দেখায় তাহলে বোঝা যাবে লেন্সটি অবতল।

একটি উত্তল লেন্সের ফোকাস দূরত্ব 5 cm। একটি সিরাপের শিশির ছোটো ছোটো অক্ষরগুলিকে তুমি পড়তে চাও, তাহলে লেন্সটিকে কোথায় রাখবে? এক্ষেত্রে প্রতিবিম্ব সৎ না অসৎ?

আমরা জানি উত্তল লেন্স ফোকাস দূরত্বের চেয়ে কম দূরত্বে থাকা কোনো বস্তুর সমশীর্ষ, বিবর্ধিত অসদবিম্ব গঠন করে। তাই সিরাপের শিশির ছোটো ছোটো অক্ষরগুলিকে পড়তে হলে লেন্সের থেকে 5 cm -এর কম দূরত্বে শিশিটাকে রেখে অপর পাশ থেকে লেন্সের মধ্য দিয়ে দেখলে লেখাগুলি বড়ো দেখাবে। এক্ষেত্রে প্রতিবিম্ব অসৎ।

একটি লেন্সকে দেয়াল থেকে 12 cm সামনে রাখলে দূরের একটি গাছের অবশীর্ষ, খর্বকায় প্রতিবিম্ব দেয়ালে গঠিত হয়। লেন্সটি কী প্রকৃতির? লেন্সের ফোকাস দূরত্বের মান কত?

লেন্সটি উত্তল। কারণ, উত্তল লেন্সের সামনে কোনো বস্তু ফোকাস দূরত্বের দ্বিগুণ বা \( 2f \) অপেক্ষা বেশি দূরত্বে থাকলে লেন্সের অপর পার্শ্বে \( f \) -এর বেশি কিন্তু \( 2f \) -এর কম দূরত্বে খর্বকায়, সদবিম্ব গঠিত হয়।

লেন্সের ফোকাস দূরত্ব প্রায় 12 cm। প্রকৃত অর্থে ফোকাস দূরত্ব 12 cm -এর চেয়ে সামান্য কম হবে।

একটি মোমবাতিকে f ফোকাস দূরত্বের একটি উত্তল লেন্সের খুব সামনে থেকে ধীরে ধীরে অনেক দূরে সরানো হল। ছকের সাহায্যে মোমবাতির অবস্থান, প্রতিবিম্বের অবস্থান ও প্রকৃতি দেখাও।

মোমবাতির অবস্থান	প্রতিবিম্বের অবস্থান	প্রতিবিম্বের প্রকৃতি
f -এর কম দূরত্বে	লেন্সের যেদিকে বস্তু সেই দিকে f -এর বেশি দূরত্বে	বিবর্ধিত, সমশীর্ষ, অসদবিম্ব
ফোকাসে	লেন্সের যেদিকে বস্তু তার অপর পাশে, অসীমে	অতিমাত্রায় বিবর্ধিত, অবশীর্ষ, সদবিম্ব
f -এর বেশি কিন্তু 2f -এর কম দূরত্বে	লেন্সের যেদিকে বস্তু তার অপর পাশে, 2f -এর বেশি দূরত্বে	বিবর্ধিত, অবশীর্ষ, সদবিম্ব
2f দূরত্বে	লেন্সের যেদিকে বস্তু তার অপর পাশে, 2f দূরত্বে	সমান সাইজের, অবশীর্ষ, সদবিম্ব
2f -এর বেশি দূরত্বে	লেন্সের যেদিকে বস্তু তার অপর পাশে, f -এর বেশি কিন্তু 2f -এর কম দূরত্বে	খর্বকায়, অবশীর্ষ, সদবিম্ব
অসীমে থাকলে	দ্বিতীয় মুখ্য ফোকাস তলে	অত্যন্ত খর্বকায়, অবশীর্ষ, সদবিম্ব

কোনো লেন্সের ফোকাস দৈর্ঘ্য কীসের ওপর নির্ভরশীল?

কোনো লেন্সের ফোকাস দৈর্ঘ্য নিম্নলিখিত বিষয়গুলির ওপর নির্ভরশীল –

• পারিপার্শ্বিক মাধ্যম সাপেক্ষে লেন্সের উপাদানের প্রতিসরাঙ্ক,
• আপতিত আলোর বর্ণ,
• লেন্সের দুই গোলীয় তলের বক্রতা ব্যাসার্ধ।

লেন্সের অনুবন্ধী ফোকাস যুগল কাকে বলে?

কোনো লেন্সের অবস্থান স্থির রেখে যদি দুটি এমন বিন্দু পাওয়া যায়, যার একটিতে বস্তু রাখলে অন্যটিতে প্রতিবিম্ব গঠিত হবে তাহলে ওই দুটি বিন্দুকে লেন্সের অনুবন্ধী ফোকাস যুগল বলে।

একটি উত্তল লেন্সের অর্ধেকটা কালো কাগজে মুড়ে দিলে বস্তুর প্রতিবিম্বের কীরূপ পরিবর্তন হবে?

লেন্সের অর্ধেকটা খোলা থাকার জন্য ওই অংশ দিয়ে আলোর প্রতিসরণ হবে এবং বস্তুর পূর্ণ প্রতিবিম্বই গঠিত হবে কিন্তু অর্ধেক অংশ দিয়ে আলোর প্রতিসরণ না হওয়ার জন্য প্রতিবিম্বের উজ্জ্বলতা হ্রাস পাবে।

সরল ক্যামেরা ও মানুষের চোখ

সরল ক্যামেরা দ্বারা কোনো বস্তুর ছবি তোলার সময় লেন্সের কোন্ অবস্থার সাহায্য নেওয়া হয়?

উত্তল লেন্সের সামনে দ্বিগুণ ফোকাস দূরত্বের চেয়ে বেশি দূরত্বে একটি বস্তু থাকলে লেন্সের অপর পাশে ফোকাস দূরত্বের চেয়ে বেশি কিন্তু দ্বিগুণ ফোকাস দূরত্বের চেয়ে কম দূরত্বে বস্তুর অবশীর্ষ, খর্বকায় সদবিম্ব গঠিত হয়। লেন্সের এই ধর্মের সাহায্যে সরল ক্যামেরায় ছবি তোলা হয়।

একটি সরল ক্যামেরার মূল অংশগুলি কী কী? চিত্রের সাহায্যে একটি সরল ক্যামেরার বিভিন্ন অংশ চিহ্নিত করো।

একটি সরল ক্যামেরার মূল অংশগুলি হল –

• আলোক-নিরুদ্ধ বাক্স
• অভিলক্ষ্য
• ডায়াফ্রাম
• শাটার
• পর্দা
• ফোটোপ্লেট

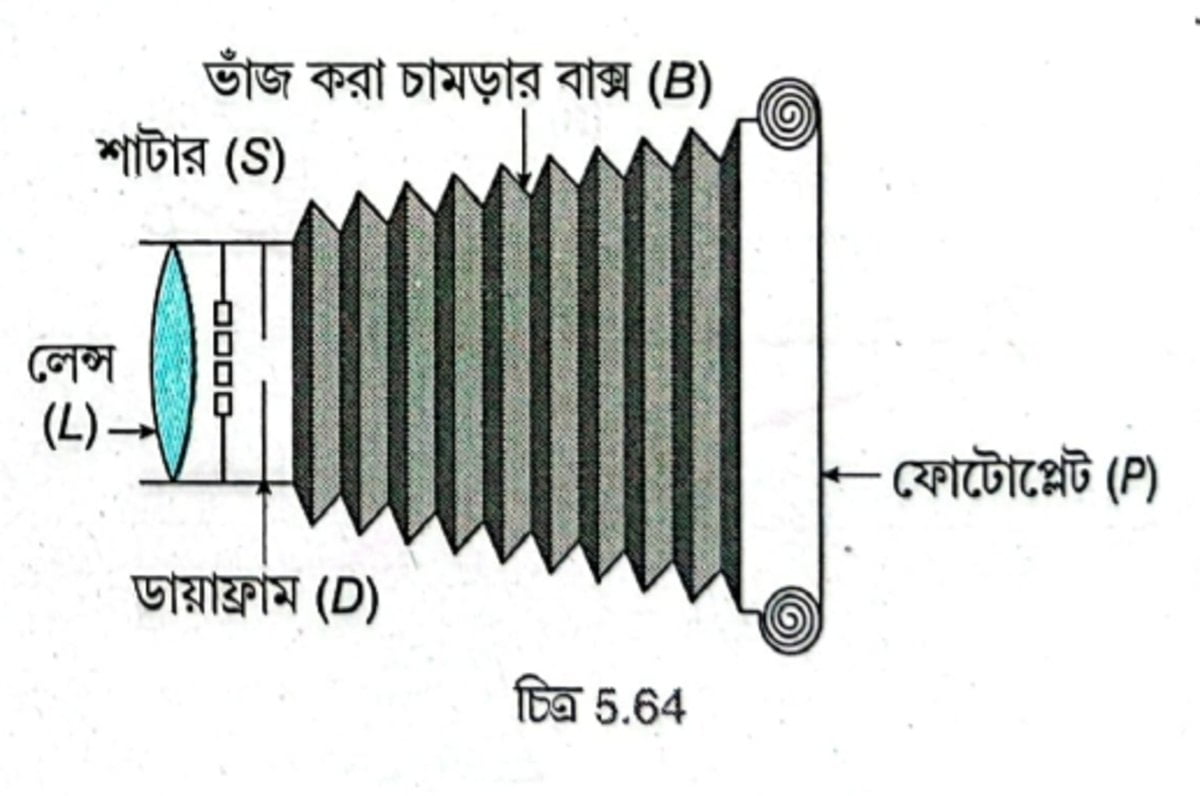
একটি সরল ক্যামেরার গঠন সংক্ষেপে বর্ণনা করো।

সরল ক্যামেরার গঠন –

একটি সরল ক্যামেরার বিভিন্ন অংশের সংক্ষিপ্ত বর্ণনা নীচে দেওয়া হল।

• আলোকনিরুদ্ধ বাক্স – একটি ভাঁজ করা চামড়ার বা শক্ত কালো কাগজের বাক্স, এর দৈর্ঘ্য প্রয়োজনমতো বাড়ানো বা কমানো যায়। এর ভিতরের অংশে কালো রং করা থাকে যাতে বাক্সের দেয়াল থেকে আলোর প্রতিফলন না হয়।
• অভিলক্ষ্য – বাক্সের সামনে উপযুক্ত ফোকাস দৈর্ঘ্যের একটি উত্তল লেন্স (L) বসানো থাকে। একে অভিলক্ষ্য বলা হয়।
• ডায়াফ্রাম – ডায়াফ্রাম (D) হল লেন্সের পিছনে একটি বৃত্তাকার ছিদ্র যা কতকগুলি ধাতব পাতের সমন্বয়ে তৈরি। ছিদ্রের ব্যাস পরিবর্তন করে ক্যামেরার ভিতর আলো প্রবেশের পরিমাণ নিয়ন্ত্রণ করা হয়। ছিদ্রের ব্যাস কম হলে লেন্সের কার্যকর উন্মেষ কম হয় এবং কম আলো প্রবেশ করলেও প্রতিবিম্ব স্পষ্ট হয়।
• শাটার – শাটারের (S) সাহায্যে ক্যামেরার মধ্যে কতটা সময় ধরে আলো প্রবেশ করবে অর্থাৎ আলোকসম্পাতকাল নিয়ন্ত্রণ করা হয়। এর সাহায্যে আলোকসম্পাতকালের সময় \( \frac1{10}s \) থেকে \( \frac1{100}s \) -এর মধ্যে রাখা যায়। ছবি ভালো হবে না খারাপ হবে তা অনেকটাই আলোকসম্পাতকালের ওপর নির্ভর করে।
• পর্দা – ক্যামেরার পিছনে যে জায়গায় ছবি তৈরি হয় সেটি হল পর্দা (P)। প্রথমে পর্দার স্থানে একটি ঘষা কাচ রেখে, শাটার খুলে ভাঁজ করা বাক্সের সাহায্যে লেন্স ও পর্দার মধ্যে দূরত্ব কমিয়ে বা বাড়িয়ে প্লেটের ওপর বস্তুর প্রতিবিম্বকে ফোকাস করা হয়। এরপর শাটার বন্ধ করে একটি ফোটোপ্লেট বা ফিল্ম পর্দার স্থানে রাখা হয়। এতে সিলভার ও হ্যালোজেনের একটি আলোক সংবেদী পদার্থের প্রলেপ দেওয়া থাকে। ফিল্ম – এ ছবি গঠিত হওয়ার পর আলোকনিরুদ্ধ একটি কাঠের বাক্সে রাখা হয়।

একটি সরল ক্যামেরায় কোনো বস্তুর কীভাবে প্রতিবিম্ব গঠিত হয় তা রশ্মিচিত্রের সাহায্যে দেখাও।

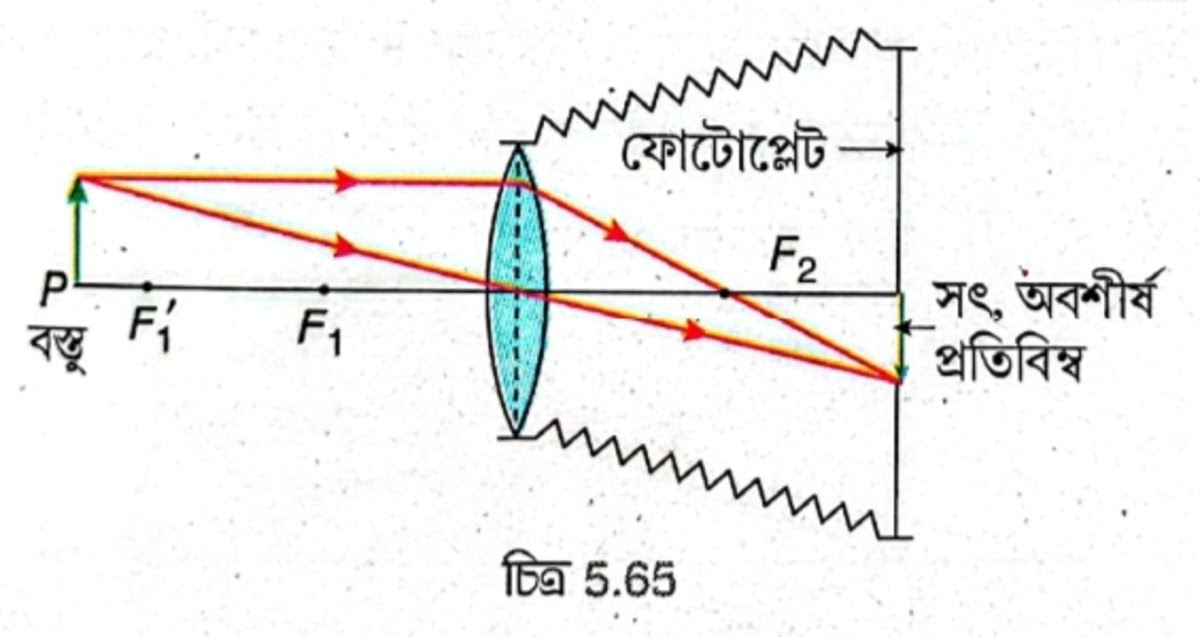
ক্যামেরায় অভিলক্ষ্যকে এগোনো বা পিছোনোর ব্যবস্থা থাকে কেন?

কোনো উত্তল লেন্সের সামনে \( 2f \) (\( f \) = ফোকাস দূরত্ব) -এর বেশি দূরত্বে কোনো বস্তু থাকলে অপর পাশে \( f \) -এর বেশি কিন্তু \( 2f \) -এর কম দূরত্বে সদবিম্ব গঠিত হয়।

উত্তল লেন্সের এই ধর্মকে কাজে লাগিয়ে সকল ক্যামেরায় ছবি তোলা হয়। ক্যামেরার সামনে বস্তু বিভিন্ন দূরত্বে থাকে তাই প্রতিবিম্ব দূরত্বও বিভিন্ন হয়। অভিলক্ষ্যকে এগিয়ে বা পিছিয়ে প্রতিবিম্ব দূরত্বকে পরিবর্তন করা হয় যাতে ফিল্ম -এর ওপর বস্তুর স্পষ্ট প্রতিবিম্ব গঠিত হয়।

মানুষের চোখের গঠন সংক্ষেপে বর্ণনা করো।

মানুষের চোখ প্রায় গোলকাকার, একে অক্ষিগোলক বলা হয়। এটি মাথার খুলির শক্ত কোটরের মধ্যে ছয়টি পেশির দ্বারা এমনভাবে আটকানো যাতে অক্ষিগোলককে ঘোরানো যায়।

শ্বেতমণ্ডল – অক্ষিগোলককে ঘিরে একটি সাদা, অস্বচ্ছ, তন্তুময় কলার আবরণ থাকে একে শ্বেতমণ্ডল বলে।

কর্ণিয়া – শ্বেতমণ্ডলের সামনে, মোটামুটি চোখের মাঝের স্বচ্ছ অংশ এবং এর বক্রতা বাকি অংশের তুলনায় বেশি। এই অংশের প্রতিসরাঙ্ক প্রায় 1.33, একে কর্নিয়া বলা হয়। কর্নিয়ার মধ্য দিয়ে চোখে আলো প্রবেশ করে।

অ্যাকোয়াস হিউমার – কর্নিয়ার পিছনে একটি প্রকোষ্ঠ আছে যা 1.33 প্রতিসরাঙ্কের একটি স্বচ্ছ, নোনতা জলীয় পদার্থ দ্বারা পূর্ণ, এই জলীয় পদার্থকে অ্যাকোয়াস হিউমার বলা হয়। এটি চোখকে স্বাভাবিকভাবে ফুলিয়ে রাখে।

আইরিস – এটি একটি গোলাকার রঙিন ঝিল্লির পর্দা যার কেন্দ্রে একটি গোলাকার ছিদ্র বা তারারন্ধ্র থাকে। চোখে কতটা আলো প্রবেশ করবে তা আইরিস নিয়ন্ত্রণ করে।

চোখের লেন্স – আইরিসের ঠিক পিছনে থাকে চোখের লেন্স যা স্বচ্ছ ও নমনীয় পদার্থ দিয়ে গঠিত। এটি একটি উভোত্তল লেন্স যার গড় প্রতিসরাঙ্ক 1.45। এই লেন্সের সামনের তলের বক্রতা ব্যাসার্ধ পিছনের তলের তুলনায় বেশি। এই লেন্সকে সঠিক অবস্থানে আটকে রাখে সাসপেন্সরি লিগামেন্ট। সিলিয়ারি পেশি, সাসপেন্সরি লিগামেন্টের সাহায্যে চোখের লেন্সের বক্রতা পরিবর্তন করে চোখের লেন্সের ফোকাস দৈর্ঘ্য পরিবর্তন করে।

রেটিনা – অক্ষিগোলকের ভিতরের স্তর যা আলোকসংবেদী কোশ, তন্ত্র ইত্যাদি দ্বারা গঠিত তাকে রেটিনা বলা হয়। চোখের লেন্স ও রেটিনার মধ্যবর্তী প্রকোষ্ঠ স্বচ্ছ, জেলির মতো পদার্থ বা ভিট্রিয়াস হিউমার দ্বারা পূর্ণ। রেটিনা চক্ষুনার্ভের সঙ্গে সরাসরি যুক্ত। রেটিনায় কোনো বস্তুর প্রতিবিম্ব গঠিত হলে সেই অনুভূতি চক্ষুনার্ভের মাধ্যমে মস্তিষ্কে পৌঁছোয় এবং আমাদের দেখার অনুভূতি জাগায়।

মানুষের চোখের চিত্র অঙ্কন করে বিভিন্ন অংশ চিহ্নিত করো এবং চোখে কোনো বস্তুর প্রতিবিম্ব গঠন রশ্মিচিত্রের সাহায্যে দেখাও।

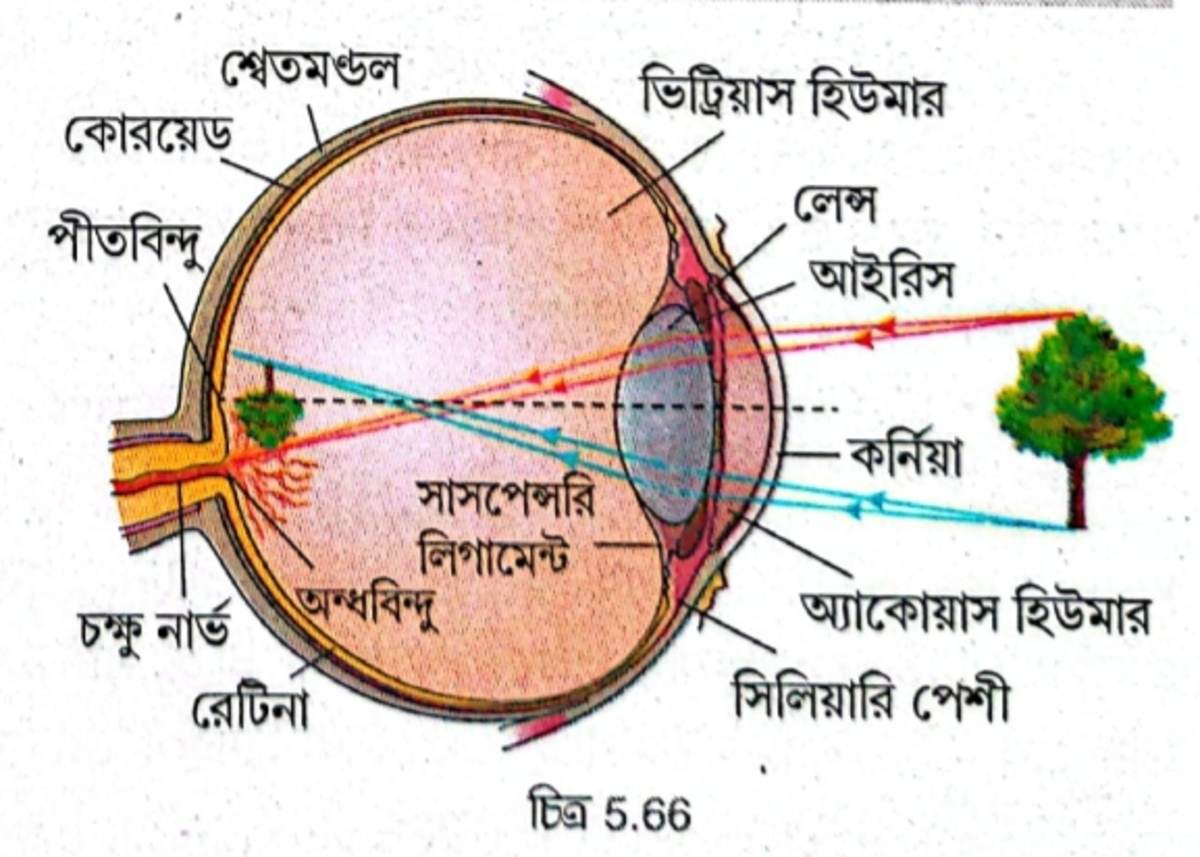
প্রত্যক্ষ দৃষ্টি ও পরোক্ষ দৃষ্টি বলতে কী বোঝ? অন্ধ বিন্দু কী?

রেটিনার মাঝখানে 2 mm ব্যাসের একটি চাপা অংশ আছে, একে পীত বিন্দু বলা হয়। পীত বিন্দুর কেন্দ্রে 0.3 mm ব্যাসের একটি গোল অংশ আছে যাকে ফোভিয়া সেন্ট্রালিস বলে। ফোভিয়া সেন্ট্রালিসে প্রতিবিম্ব গঠিত হলে তার স্পষ্টতা হয় সবচেয়ে বেশি, একে প্রত্যক্ষ দৃষ্টি বলা হয়। রেটিনার অন্যান্য অংশে গঠিত প্রতিবিম্ব অত স্পষ্ট হয় না, এই দেখাকে পরোক্ষ দৃষ্টি বলা হয়।

চক্ষুনার্ভগুলি রেটিনার যে অংশে যুক্ত সেখানে প্রতিবিম্ব গঠিত হলে দর্শনের অনুভূতি সৃষ্টি হয় না, একে অন্ধ বিন্দু বলা হয়।

মানুষের চোখে কীভাবে প্রতিবিম্ব গঠিত হয়?

আমরা যখন কোনো বস্তু দেখি তখন বস্তু থেকে আলোকরশ্মি কর্নিয়া, অ্যাকুয়াস হিউমার হয়ে চক্ষুলেন্সের ওপর আপতিত হয়। চক্ষুলেন্স দ্বারা প্রতিসরণের পর ভিট্রিয়াস হিউমারের মধ্য দিয়ে গিয়ে রেটিনার ওপর বস্তুর সৎ, অবশীর্ষ [চিত্র 5.63] প্রতিবিম্ব গঠিত হয়। রেটিনায় আলোকসুবেদী রড কোশ ও কোন কোশ আলোকরশ্মিতে উদ্দীপিত হয় এবং এই উদ্দীপনা চক্ষুনার্ভের মাধ্যমে সেরিব্রামের অক্সিপিটাল খণ্ডের ভিশুয়াল কর্টেক্স অংশে পৌঁছোয়। প্রতিবিম্ব উলটো হলেও মস্তিষ্কের বিশেষ প্রক্রিয়া বস্তুকে সোজাভাবে দেখতে সাহায্য করে।

রেটিনার অন্ধ বিন্দুতে কোনো প্রতিবিম্ব গঠিত হলে দর্শনের কোনো অনুভূতি সৃষ্টি হয় না কেন?

অপটিক স্নায়ুগুলি রেটিনার সঙ্গে অন্ধ বিন্দুতে যুক্ত থাকে। সেখানে রড কোশ ও কোন কোশ থাকে না। ফলে রেটিনার অন্ধ বিন্দুতে কোনো প্রতিবিম্ব গঠিত হলে দর্শনের কোনো অনুভূতি সৃষ্টি হয় না।

চোখের উপযোজন ও অভিযোজন কাকে বলে?

চোখের উপযোজন – সিলিয়ারি মাংসপেশির সাসপেন্সরি বন্ধনীর সংকোচন ও প্রসারণের ফলে চক্ষুলেন্সের ফোকাস দৈর্ঘ্য বৃদ্ধি ও হ্রাস করে দূরের ও কাছের বস্তুর প্রতিবিম্বকে রেটিনায় গঠন করার ক্ষমতাকে চোখের উপযোজন বলা হয়।

চোখের অভিযোজন – চোখের মণি স্বয়ংক্রিয়ভাবে ছোটো বা বড়ো হয়ে চোখে প্রবিষ্ট আলোর পরিমাণ নিয়ন্ত্রণ করে। চোখের এই ক্ষমতাকে অভিযোজন বলে।

দৃষ্টি নির্বন্ধ ও দ্বিনেত্র দৃষ্টি কাকে বলে?

দৃষ্টি নির্বন্ধ – কোনো বস্তুকে দেখার সময় রেটিনায় বস্তুর প্রতিবিম্ব গঠিত হলে চক্ষুনার্ভ মস্তিষ্কে যে দর্শনানুভূতির সৃষ্টি করে তার রেশ \( \frac1{10}s \) স্থায়ী থাকে। এই ঘটনাকে দৃষ্টি নির্বন্ধ বলা হয়।

দ্বিনেত্র দৃষ্টি – আমরা যখন দুটি চোখের সাহায্যে একটি বস্তুকে দেখি তখন বস্তু সাপেক্ষে দুটি চোখের অবস্থান আলাদা হওয়ার জন্য দুটি চোখের দু-রকম প্রতিবিম্ব গঠিত হয়। মস্তিষ্ক এক বিশেষ প্রক্রিয়ায় এই দুই প্রতিবিম্বকে একত্রিত করে একটি অনুভূতির সৃষ্টি করে। ফলে বস্তুর ত্রিমাত্রিক গঠন সম্পর্কে একটি স্পষ্ট ধারণা হয়। একে দ্বিনেত্র দৃষ্টি বলে।

চোখের নিকট বিন্দু, দূর বিন্দু ও দৃষ্টি পাল্লার সংজ্ঞা লেখো এবং সুস্থ চোখের ক্ষেত্রে এদের মান কত?

নিকট বিন্দু – উপযোজন প্রয়োগ করে চোখ থেকে সর্বাপেক্ষা নিকটতম যে বিন্দু পর্যন্ত একটি বস্তুকে স্পষ্টভাবে দেখতে পাওয়া যায় তাকে চোখের নিকট বিন্দু বলে। সুস্থ চোখের ক্ষেত্রে নিকট বিন্দুর দূরত্ব প্রায় 25 cm।

দূর বিন্দু – উপযোজন প্রয়োগ না করে চোখ থেকে সর্বাপেক্ষা দূরের যে বিন্দু পর্যন্ত একটি বস্তুকে স্পষ্টভাবে দেখতে পাওয়া যায় তাকে চোখের দূর বিন্দু বলে। সুস্থ চোখের ক্ষেত্রে দূর বিন্দু অসীমে অবস্থিত হয়।

দৃষ্টি পাল্লা – চোখের নিকট বিন্দু থেকে দূর বিন্দু পর্যন্ত দূরত্বকে দৃষ্টি পাল্লা বলে। সুস্থ চোখের ক্ষেত্রে দৃষ্টি পাল্লা 25 cm থেকে অসীম পর্যন্ত।

দীর্ঘ দৃষ্টি ত্রুটি চিত্রসহ ব্যাখ্যা করো।

যদি চোখ দূরের জিনিস স্পষ্ট দেখতে পায় কিন্তু কাছের জিনিস দেখতে না পায় তাহলে এই ধরনের ত্রুটিকে দীর্ঘ দৃষ্টি বলা হয়। কোনো ব্যক্তির চোখের নিকট বিন্দু দূরে সরে গেলে এই ত্রুটি দেখা যায়।

মনে করি, \( N \) হল স্বাভাবিক চোখের নিকট বিন্দু। এখানে \( N \) বিন্দুর প্রতিবিম্ব রেটিনায় গঠিত না হয়ে রেটিনার পিছনে গঠিত হয় [চিত্র 5.67] এবং চোখ সর্বোচ্চ উপযোজন প্রয়োগ করে সর্বাপেক্ষা নিকটতম \( N’ \) বিন্দুর প্রতিবিম্ব রেটিনায় গঠন করে। \( N’ \) হল দীর্ঘ দৃষ্টি ত্রুটিসম্পন্ন চোখের নিকট বিন্দু।

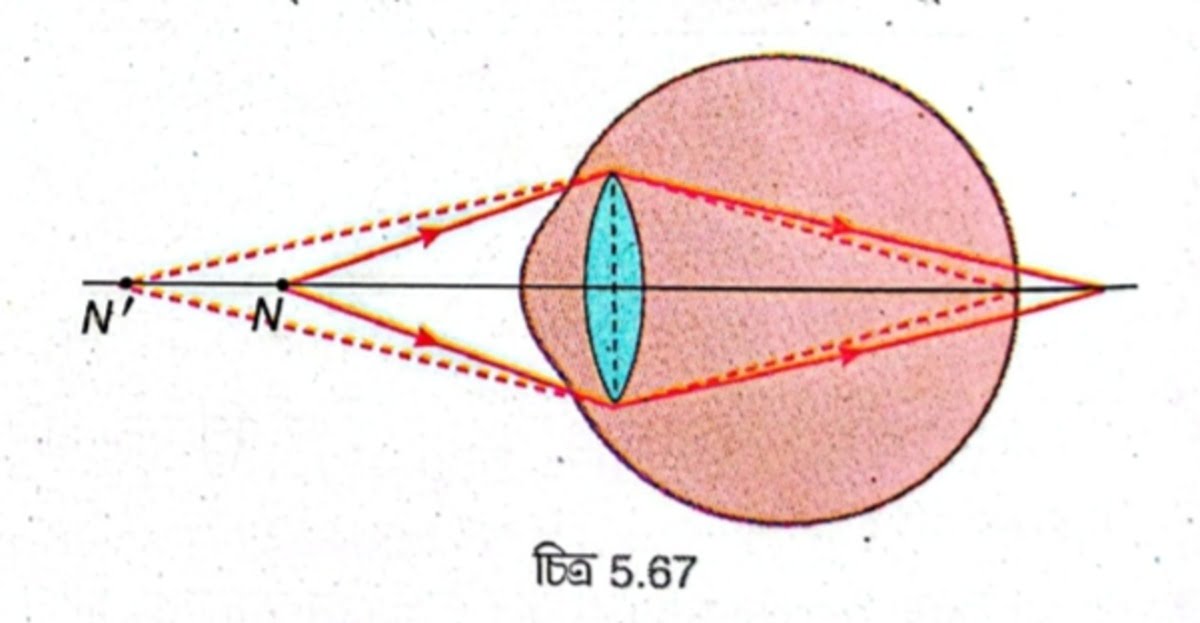
দীর্ঘ দৃষ্টির কারণগুলি লেখো।

দীর্ঘ দৃষ্টির কারণ –

• অক্ষিগোলকের আকার স্বাভাবিকের তুলনায় ছোটো হলে
• চোখের লেন্সের ফোকাস দৈর্ঘ্য স্বাভাবিকের তুলনায় বেশি হলে।

দীর্ঘ দৃষ্টি ত্রুটির প্রতিকার চিত্রসহ লেখো।

উপযুক্ত ফোকাস দৈর্ঘ্যের উত্তল লেন্সযুক্ত চশমা ব্যবহার করলে দীর্ঘ দৃষ্টি ত্রুটি দূর করা যায়।

মনে করি, দীর্ঘ দৃষ্টি ত্রুটিযুক্ত কোনো ব্যক্তির নিকট বিন্দু \( N’ \) এবং সুস্থ চোখের নিকট বিন্দু \( N \) [চিত্র 5.68]। উত্তল লেন্সটির ফোকাস দৈর্ঘ্য এমন হবে যাতে, লেন্স দ্বারা প্রতিসরণের পর \( N \) বিন্দুর অসদবিম্ব \( N’ \) বিন্দুতে গঠিত হয়। ফলে ব্যক্তি \( N \) বিন্দুকে \( N’ \) বিন্দুতে দেখে।

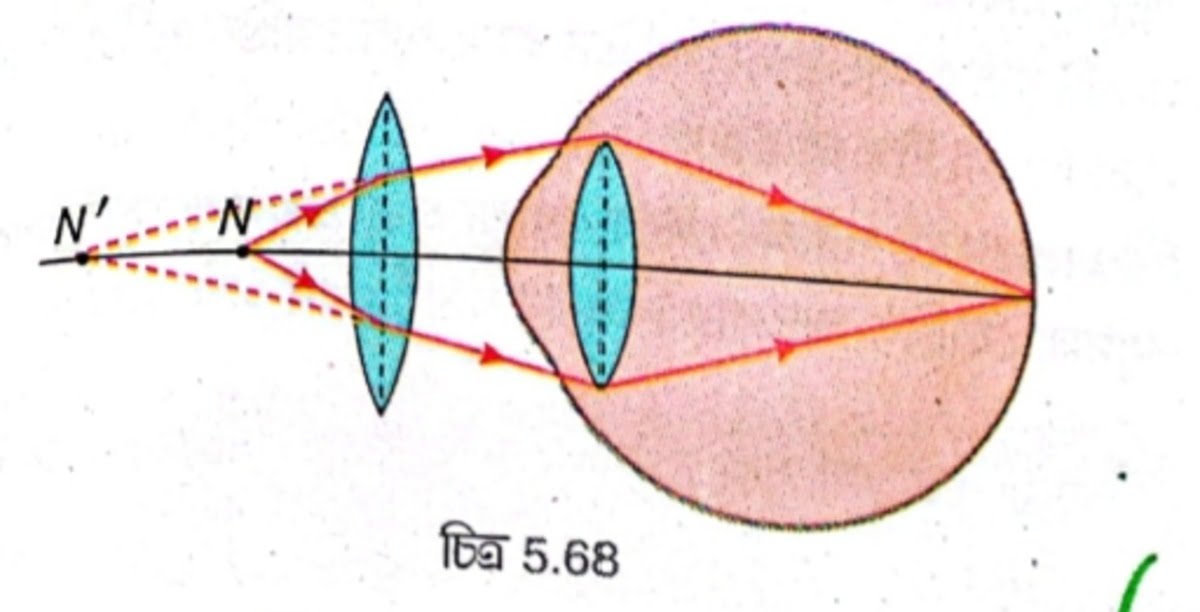
হ্রস্ব দৃষ্টি ত্রুটি চিত্রসহ ব্যাখ্যা করো।

যদি চোখ কাছের জিনিস স্পষ্ট দেখতে পায় কিন্তু দূর বিন্দু অসীমের পরিবর্তে চোখের কাছে সরে আসার জন্য দূরের জিনিস স্পষ্ট দেখতে না পায় তাহলে চোখের এই ধরনের ত্রুটিকে হ্রস্ব দৃষ্টি বলা হয়।

দূরবর্তী বস্তু থেকে আসা সমান্তরাল রশ্মিগুচ্ছ চোখের লেন্স দ্বারা প্রতিসরণের পর রেটিনায় মিলিত না হয়ে রেটিনার সামনে একটি বিন্দু A -তে মিলিত হয় [চিত্র 5.69]। এক্ষেত্রে দূর বিন্দু অসীমে অবস্থিত না হয়ে চোখের সামনে কোনো বিন্দুতে (যেমন চিত্র 5:69 -তে F) সরে আসে।

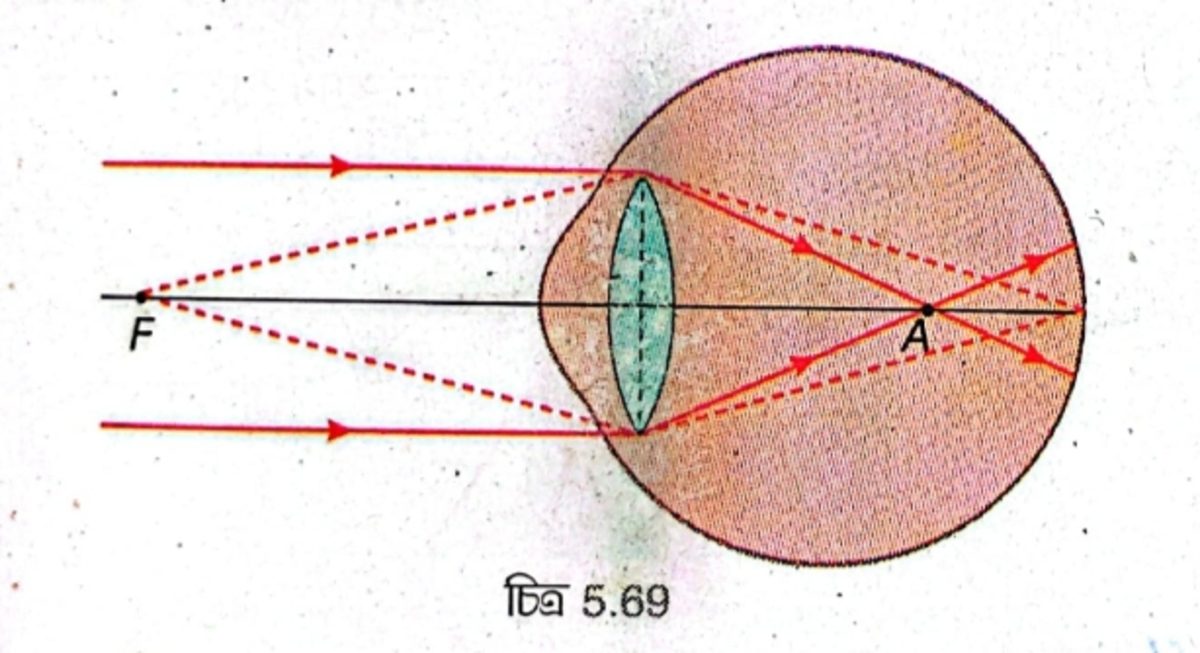
হ্রস্ব দৃষ্টির কারণগুলি লেখো।

হ্রস্ব দৃষ্টির কারণ –

• অক্ষিগোলকের আকার স্বাভাবিকের তুলনায় বড়ো হলে এবং
• চোখের লেন্সের ফোকাস দৈর্ঘ্য স্বাভাবিকের তুলনায় কম হলে।

হ্রস্ব দৃষ্টি ত্রুটির প্রতিকার চিত্রসহ লেখো।

উপযুক্ত ফোকাস দৈর্ঘ্যের অবতল লেন্সযুক্ত চশমা ব্যবহার করলে হ্রস্ব দৃষ্টি ত্রুটি দূর করা যায়।

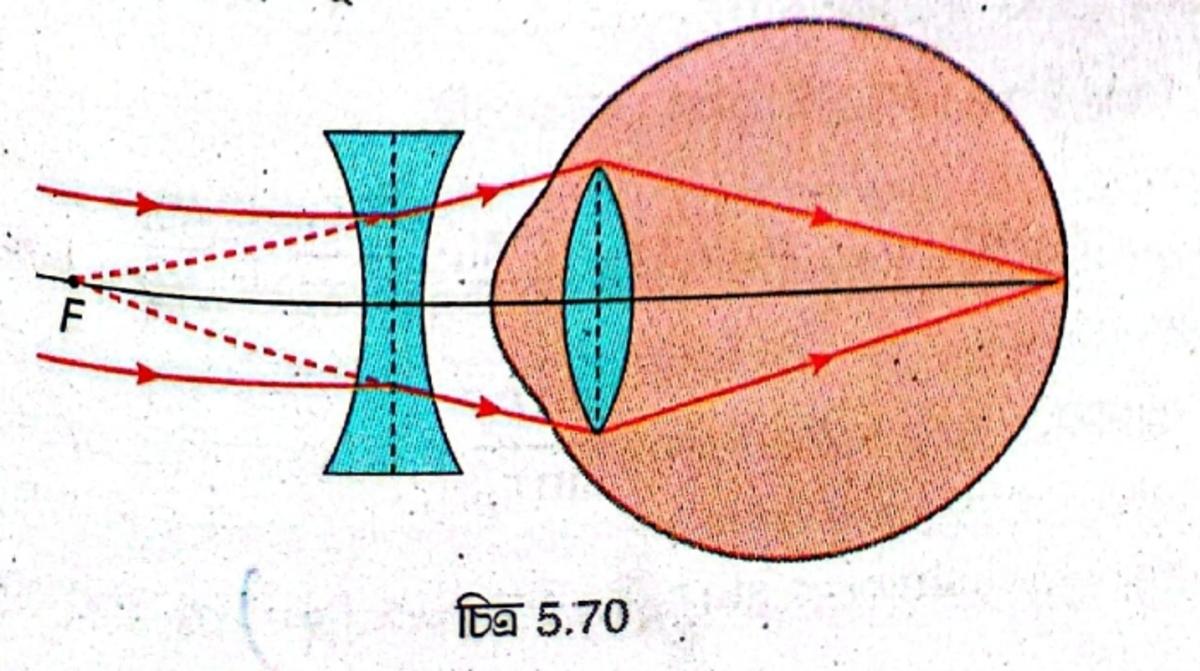
অবতল লেন্সটির ফোকাস দৈর্ঘ্য এমন হবে যাতে দূরবর্তী কোনো বস্তু থেকে আগত সমান্তরাল রশ্মিগুচ্ছ, অবতল লেন্স দ্বারা প্রতিসরণের পর মনে হবে F বিন্দু থেকে অপসৃত হচ্ছে এবং প্রতিবিম্ব রেটিনায় গঠিত হবে [চিত্র 5.70]।

চোখ ও ক্যামেরার মধ্যে পার্থক্য লেখো।

চোখ ও ক্যামেরার মধ্যে পার্থক্য –

চোখ	ক্যামেরা
1. চোখের লেন্সের ফোকাস দৈর্ঘ্য পরিবর্তন করা যায়।	1. ক্যামেরার অভিলক্ষ্যের ফোকাস দৈর্ঘ্য নির্দিষ্ট।
2. চোখের লেন্স ও পর্দা বা রেটিনার মধ্যে দূরত্ব নির্দিষ্ট।	2. ক্যামেরার অভিলক্ষ্য ও পর্দা বা ফিল্ম -এর দূরত্ব পরিবর্তন করা যায়।
3. চোখের রেটিনায় অসংখ্য প্রতিবিম্ব গঠিত হয় তবে কোনো প্রতিবিম্বই স্থায়ী নয়।	3. ক্যামেরায় একটি ফিল্মে একটিই প্রতিবিম্ব গঠিত হয় এবং সেই প্রতিবিম্ব থেকে স্থায়ী ছবি পাওয়া যায়।
4. চোখের দৃষ্টিক্ষেত্র প্রায় 150°।	4. ক্যামেরার দৃষ্টিক্ষেত্র প্রায় 60°।

আলোর বিচ্ছুরণ, বর্ণের অনুভূতি, তড়িৎচুম্বকীয় বর্ণালি ও আলোর বিক্ষেপণ

আলোর বিচ্ছুরণ কাকে বলে?

বহুবর্ণী বা কোনো যৌগিক আলোকরশ্মি কোনো প্রতিসারক মাধ্যমের মধ্য দিয়ে গেলে বিভিন্ন বর্ণে ভেঙে যায়। এই ঘটনাকে আলোর বিচ্ছুরণ বলা হয়।

বর্ণালি কাকে বলে? সাদা আলোর বর্ণালি রঙের ক্রম কী ধরনের থাকে?

বহুবর্ণী বা কোনো যৌগিক আলোর বিচ্ছুরণের ফলে বিভিন্ন বর্ণের আলোর যে পটি পাওয়া যায় তাকে বর্ণালি বলা হয়।

প্রিজমের মধ্য দিয়ে সাদা আলোর বিচ্ছুরণের ফলে পর্দায় যে বর্ণালি উৎপন্ন হয় তার একদম ওপরে দেখা যায় লাল বর্ণ এবং একদম নীচে থাকে বেগুনি বর্ণ। নীচ থেকে ওপরদিকে বর্ণগুলি যেভাবে সাজানো থাকে তা হল – বেগুনি, নীল, আকাশি, সবুজ, হলুদ, কমলা ও লাল। বাংলায় বেনীআসহকলা ও ইংরাজীতে VIBGYOR শব্দটি বলা হয় নীচ থেকে ওপরের দিকের বর্ণালির বিভিন্ন রং -কে পরপর মনে রাখার জন্য।

VIBGYOR -এর অর্থ কী?

VIBGYOR -এর অর্থ –

V – Violet (বেগুনি),
I – Indigo (নীল),
B – Blue (আকাশি নীল),
G – Green (সবুজ),
Y – Yellow (হলুদ),
O – Orange (কমলা),
R – Red (লাল)

একটি সহজ পরীক্ষার সাহায্যে আলোর বিচ্ছুরণ দেখাও।

একটি বড়ো কার্ডবোর্ড নিয়ে তার মাঝে একটি ছোটো ছিদ্র করা হল। এবার একটি টেবিলের ওপর একটি প্রিজম রেখে টেবিলটিকে সূর্যালোকে রাখা হল। এবার টেবিলের ওপরটা ভালো করে ঢেকে কার্ডবোর্ডটিকে প্রিজমের সামনে এমনভাবে রাখা হল যাতে কার্ডবোর্ডের ছোটো ছিদ্রের মধ্য দিয়ে সূর্যালোক প্রবেশ করে প্রিজমের প্রতিসারক তলে আপতিত হয়। এখন প্রিজমের অপর প্রতিসারক তলের সামনে একটি পর্দা রাখা হলে পর্দায় একটি রঙিন পটি দেখা যাবে। নীচের দিক থেকে পটির রংগুলি হল বেগুনি, নীল, আকাশি, সবুজ, হলুদ, কমলা ও লাল।

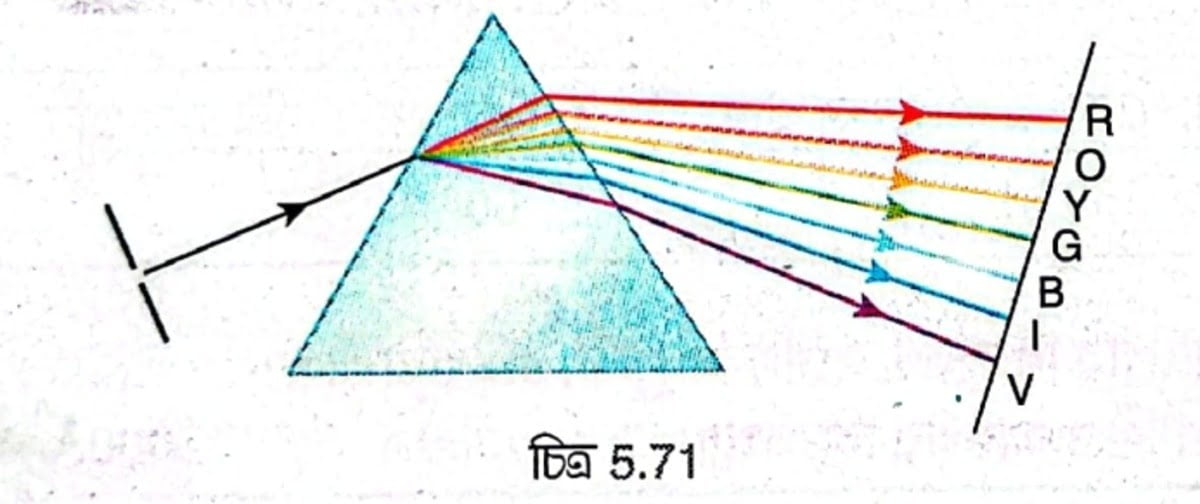
সিদ্ধান্ত – সাদা আলো যৌগিক আলো, তাই প্রিজমের মধ্য দিয়ে যাওয়ার ফলে আলোর বিচ্ছুরণের জন্য সাতটি বর্ণে ভেঙে যায়।

প্রিজম বর্ণ সৃষ্টি করে না শুধুমাত্র যৌগিক আলোর বিচ্ছুরণ ঘটায় – একটি পরীক্ষার সাহায্যে দেখাও।

দুটি অভিন্ন প্রিজম \( ABC \) ও \( A’B’C’ \) নেওয়া হল। প্রিজম দুটিকে সূর্যালোকে টেবিলের ওপর পাশাপাশি উলটো করে এমনভাবে বসানো হল যাতে প্রিজম দুটির প্রতিসারক তল পরস্পর সমান্তরাল থাকে। এরপর একটি বড়ো কার্ডবোর্ড নিয়ে তার মাঝে একটি ছোটো ছিদ্র করা হল। টেবিলের ওপরটা ভালো করে ঢেকে কার্ডবোর্ডটিকে \( ABC \) প্রিজমের সামনে এমনভাবে রাখা হল যাতে কার্ডবোর্ডের ছোটো ছিদ্রের মধ্য দিয়ে সূর্যালোক প্রবেশ করে প্রিজমের প্রতিসারক তলে আপতিত হয়। প্রথম প্রিজম থেকে প্রতিসরণের পর সাদা রশ্মি সাতটি বর্ণের আলোয় ভেঙে যায় এবং দ্বিতীয় প্রিজমের মধ্য দিয়ে যাওয়ার পর আবার সাতটি বর্ণের আলো সংযোজিত হয়ে পর্দায় রঙিন পটির পরিবর্তে সাদা আলো উৎপন্ন হয়।

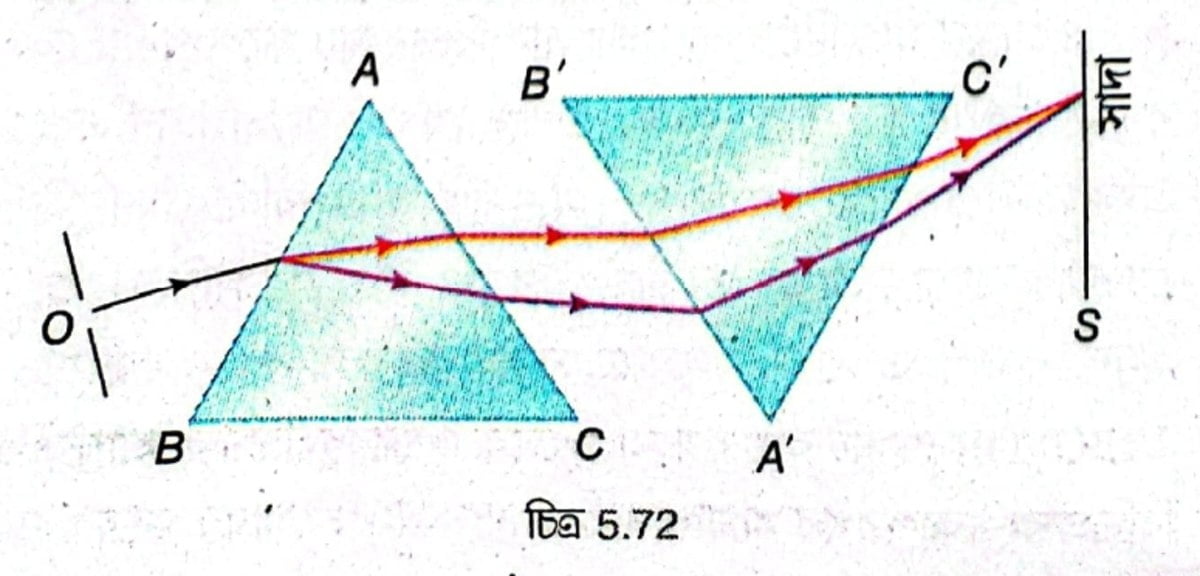
সিদ্ধান্ত – এই পরীক্ষা থেকে বোঝা যায় প্রিজম বর্ণ সৃষ্টি করে না, শুধুমাত্র যৌগিক আলোর বিচ্ছুরণ ঘটায়।

স্নেলের সূত্রের সাহায্যে আলোর বিচ্ছুরণের ব্যাখ্যা দাও।

শূন্যস্থানে আলোর বেগ \( =c \), কোনো মাধ্যমে আলোর বেগ \( =v \) হলে ওই মাধ্যমের প্রতিসরাঙ্ক \( \mu=\frac cv \)। শূন্যস্থানে সব বর্ণের আলোই একই বেগে \(\left(3\times10^8\;m/s\right) \) যায় কিন্তু অন্য কোনো নির্দিষ্ট স্বচ্ছ মাধ্যমে সব বর্ণের আলোর বেগ বিভিন্ন। ওই মাধ্যমে সব বর্ণের আলো প্রবেশ করলে সাদা আলোর সাতটি বর্ণের আলোর মধ্যে লাল বর্ণের আলোর বেগ সবচেয়ে বেশি এবং বেগুনি বর্ণের আলোর বেগ সবচেয়ে কম হয়। তাই ওই মাধ্যমের প্রতিসরাঙ্ক লাল বর্ণের আলোর জন্য সবচেয়ে কম ও বেগুনি বর্ণের আলোর জন্য সবচেয়ে বেশি অর্থাৎ \( \mu_R<\mu_O<\mu_Y<\mu_G<\mu_B<\mu_I<\mu_V \) হয়।

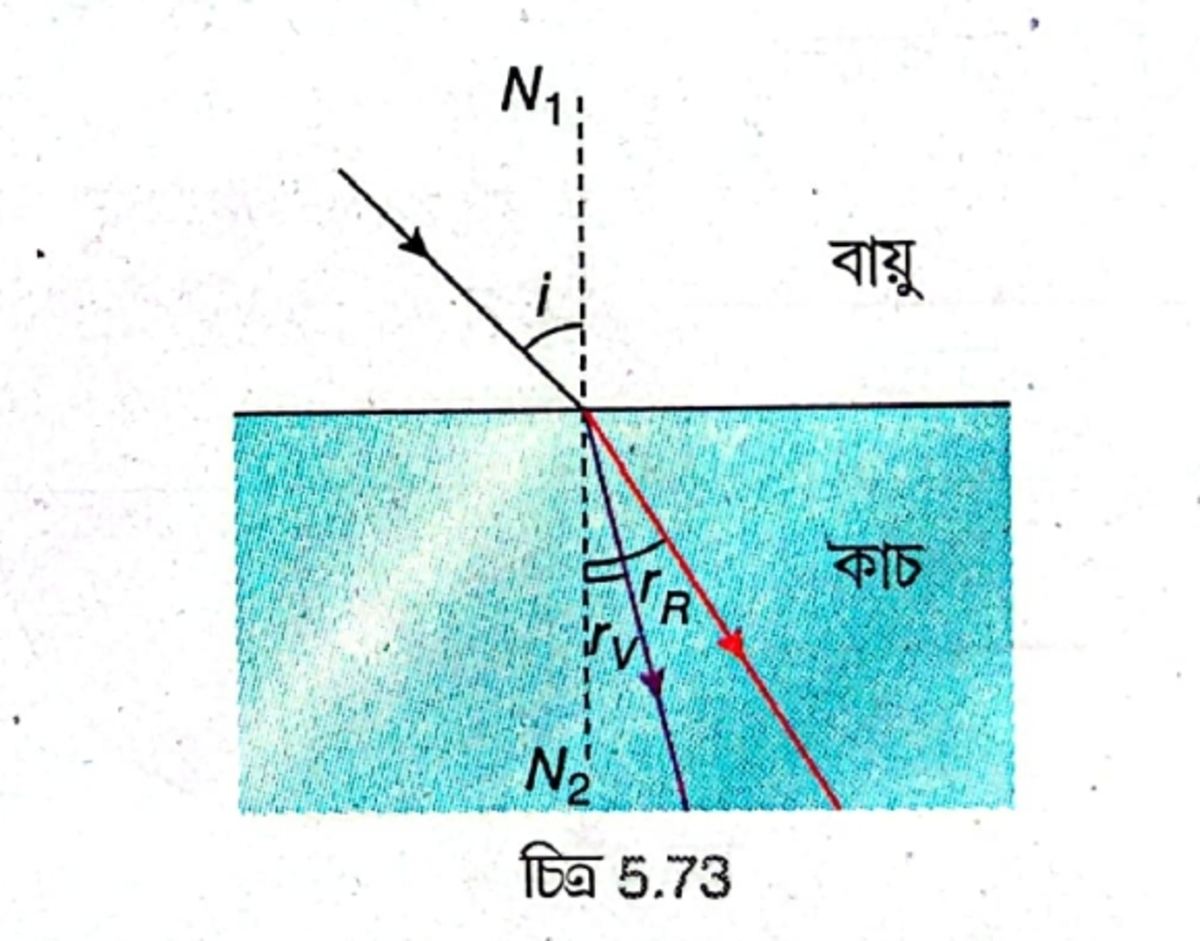
মনে করি, লাল ও বেগুনি বর্ণের দুটি আলোকরশ্মি বায়ু থেকে বায়ু ও কাচ মাধ্যমের বিভেদতলে i কোণে আপতিত হল [চিত্র 5.73]। লাল ও বেগুনি বর্ণের জন্য কাচের প্রতিসরাঙ্ক যথাক্রমে \( \mu_R \) ও \( \mu_V \) এবং প্রতিসরণ কোণ যথাক্রমে \( r_R \) ও \( r_V \) হলে স্নেলের সূত্র থেকে পাই, লাল আলোর জন্য, \( \frac{\sin i}{\sin r_R}=\mu_R \)

বা, \( \sin i=\mu_R\cdot\sin r_R \) …………. (1)

এবং বেগুনি আলোর জন্য, \( \frac{\sin i}{\sin r_V}=\mu_V \)

বা, \( \sin i=\mu_V\cdot\sin r_V \) …………. (2)

(1) ও (2) নং সমীকরণ থেকে পাই,

\( \mu_V\sin r_V=\mu_R\sin r_R \)

বা, \( \frac{\sin r_V}{\sin r_R}=\frac{\mu_R}{\mu_V} \)

আবার, \( \mu_R<\mu_V \)

∴ \( \frac{\sin r_V}{\sin r_R}<1 \)

বা, \( \sin r_V<\sin r_R \)

বা, \( r_V<r_R \)

অর্থাৎ কাচ মাধ্যমে বেগুনি বর্ণের আলোর প্রতিসরণ কোণ সবচেয়ে কম ও লাল আলোর প্রতিসরণ কোণ সবচেয়ে বেশি হবে। সুতরাং, সাদা আলো একইভাবে আপতিত হলে প্রতিসরণের পর সাতটি বর্ণের আলোকরশ্মির প্রত্যেকের প্রতিসরণ কোণ আলাদা হওয়ার জন্য রশ্মিগুলি ভেঙে যাবে। এটিই হল আলোর বিচ্ছুরণ।

একটি আয়তাকার কাচের স্ল্যাবের ওপর সাদা আলো পড়লে তার বিচ্ছুরণ হয় না কেন?

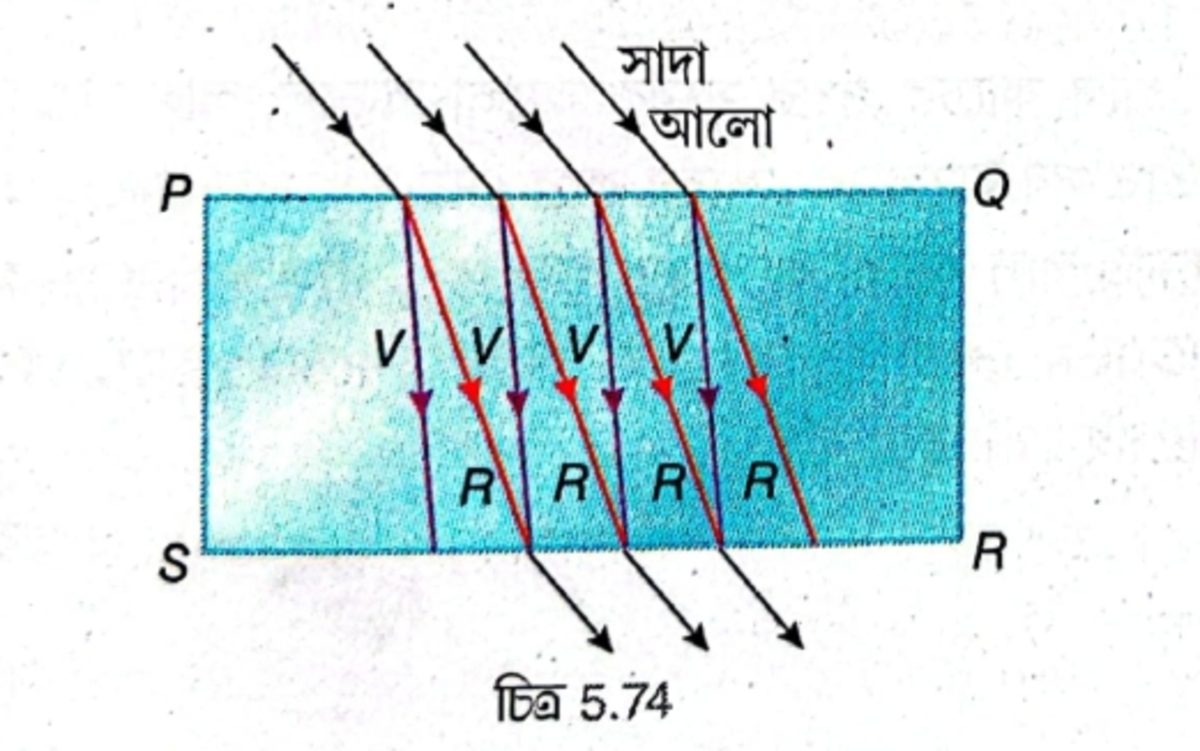
মনে করি, একটি আয়তাকার কাচের স্ল্যাব \( PQRS \) [চিত্র 5.74] -এর \( PQ \) পার্শ্বে সাদা আলো আপতিত হল। সাদা আলোর সাতটি বর্ণের জন্য কাচের আলাদা প্রতিসরাঙ্ক হওয়ায় \( PQ \) বিভেদতলে রশ্মিগুলির বিচ্ছুরণ হবে, অর্থাৎ একপ্রান্তে বেগুনি আলো ও অন্য প্রান্তে লাল আলো থাকবে। চিত্রে এদের যথাক্রমে \( V \) ও \( R \) দ্বারা দেখানো হয়েছে। কিন্তু \( SR \) পার্শ্ব থেকে নির্গত হওয়ার পর সমস্ত রশ্মি আপতিত রশ্মির সমান্তরাল হবে এবং সংযুক্ত হয়ে আবার সাদা আলো গঠন করবে। তাই আয়তাকার কাচের স্ল্যাবে আলোর বিচ্ছুরণ দেখা যাবে না।

বিকল্প উত্তর – মনে করি, একটি আয়তাকার কাচের স্ল্যাব \( PQRS\) -এর \( PQ \) পার্শ্বে সাদা আলো আপতিত হল। আয়তাকার কাচের স্ল্যাবকে \( PQS \) ও \( SQR \) প্রধান ছেদের দুটো প্রিজমের সমষ্টি হিসেবে বিবেচনা করা হলে \( PQS \) প্রিজম সাদা আলোকে বিচ্ছুরিত করবে এবং \( SQR \) প্রিজম উলটোভাবে থাকায় এই বিচ্ছুরিত রশ্মিগুলিকে সংযুক্ত করে আবার সাদা আলোয় রূপান্তরিত করবে তাই আয়তাকার কাচের স্ল্যাবে আলোর বিচ্ছুরণ দেখা যাবে না।

প্রিজমের কোনো প্রতিসারক তলে সাদা আলো আপতিত হলে, অপর প্রতিসারক তলের সামনে কোনো পর্দা রাখলে পর্দায় সাতটি রং দেখা যায় কেন?

সাদা আলো সাতটি বর্ণের সমষ্টি। এই সাতটি বর্ণের জন্য কাচের প্রতিসরাঙ্ক আলাদা – লাল বর্ণের জন্য সবচেয়ে কম ও বেগুনি বর্ণের জন্য সবচেয়ে বেশি। প্রিজমের ওপর সাদা আলো ফেলা হলে অর্থাৎ সাতটি বর্ণের আলোই একই কোণে আপতিত হলে প্রথম প্রতিসারক তলে প্রতিসরণের পর সাতটি বর্ণের আলোর প্রতিসরণ কোণ বা চ্যুতিকোণ সাত রকম হবে এবং দ্বিতীয় প্রতিসারক তলে প্রতিসরণের সময় তাদের চ্যুতি আরও বেড়ে যায়, তাই পর্দায় সাতটি বর্ণের আলো দেখতে পাওয়া যায়।

রামধনু কী?

রামধনু হল আলোর বিচ্ছুরণের একটি প্রাকৃতিক দৃষ্টান্ত। সূর্যের আলো বাতাসে ভাসমান জলকণার মধ্য দিয়ে যাওয়ার সময় বিচ্ছুরিত হয় এবং সূর্যের দিকে পিছন করে দাঁড়ালে রামধনু দেখা যায়। এই রামধনুর বৃত্তচাপের ওপরের দিকে লাল রং ও ভিতরের নীচের দিকে থাকে বেগুনি রং। এই ধরনের রামধনু হল প্রথম ক্রমের রামধনু। আবার মাঝে মাঝে এই রামধনুর একটু ওপরে কম উজ্জ্বলতার আর-একটি রামধনু দেখা যায় যার বৃত্তচাপের ওপরের রং বেগুনি ও নীচের দিকের রং লাল। এই ধরনের রামধনু হল দ্বিতীয় ক্রমের রামধনু।

দৃশ্যমান বর্ণালি কাকে বলে?

যে সমস্ত আলোর তরঙ্গদৈর্ঘ্য 4000Å থেকে 8000Å -এর মধ্যে, সেই আলো আমাদের চোখে দর্শনের অনুভূতি জাগায় এই পাল্লার আলোই হল দৃশ্যমান বর্ণালি।

কোনো অস্বচ্ছ বস্তুর বর্ণ কেমন হয় তা উদাহরণসহ লেখো।

কোনো অস্বচ্ছ বস্তু সূর্যালোকে থাকলে ওই বস্তু যে বর্ণের আলোকে প্রতিফলিত করে, বস্তুকে সেই বর্ণের বলে মনে হয়। যদি বস্তু একাধিক বর্ণের আলো প্রতিফলিত করে তাহলে ওই বর্ণগুলির মিশ্রণে যে বর্ণের উৎপত্তি হয় বস্তুর বর্ণও সেটাই মনে হয়।

উদাহরণস্বরূপ বলা যায়, জবা ফুলের ওপর সূর্যালোক আপতিত হলে জবা ফুল লাল আলো ব্যতীত সব আলো শোষণ করে নেয়, শুধুমাত্র লাল আলোকেই প্রতিফলিত করে তাই জবা ফুলকে লাল লাগে। আবার সবুজ পাতাকে সবুজ লাগে কারণ সূর্যালোক পাতায় পড়লে পাতা শুধুমাত্র সবুজ আলোকেই প্রতিফলিত করে।

কোনো স্বচ্ছ বস্তুর বর্ণ কেমন হয় তা উদাহরণসহ লেখো।

কোনো স্বচ্ছ বস্তুর (যেমন – বায়ু, জল, কাচ) মধ্য দিয়ে যে বর্ণের আলো সংবাহিত হয়, বস্তুকে সেই বর্ণের মনে হয়।

উদাহরণস্বরূপ, লাল কাচের মধ্য দিয়ে শুধুমাত্র লাল বর্ণের আলোই যেতে পারে অন্য কোনো বর্ণের আলো গেলে তা শোষিত হয়, এই জন্য ওই কাচকে লাল দেখায়। আবার লাল কাচের নীচে একটি নীল কাচকে রেখে ওপর থেকে দেখলে নীল কাচকে কালো দেখায়, কারণ লাল কাচের মধ্য দিয়ে নীল আলো গেলে লাল কাচ তা শোষণ করে নেয়।

লাল কাচকে খুব গুঁড়ো করলে রং অনেক হালকা লাগে কেন?

লাল কাচ, লাল ব্যতীত অন্য সব রঙের আলো শোষণ করে নেয়। সূর্যালোকে ওই কাচগুঁড়ো রাখলে বেশিরভাগ রশ্মি প্রতিফলিত হয় আর কিছু রশ্মি টুকরোর একপ্রান্ত দিয়ে প্রবেশ করে অন্য প্রান্ত দিয়ে নির্গত হয়। কিন্তু সেক্ষেত্রে বেধ খুব কম হলে আলোর শোষণ হয় না। শুধুমাত্র যে সমস্ত টুকরোর বেধ বেশি সেখানে লাল ব্যতীত সব আলো শোষিত হয়। তাই লাল কাচ গুঁড়োর রং অনেক হালকা লাগে।

রাত্রিতে নীল আলোয় আলোকিত কোনো ঘরে লাল জবা ফুলকে কেমন দেখাবে?

রাত্রিতে নীল আলোয় আলোকিত কোনো ঘরে লাল জবা ফুলকে দেখলে, জবা ফুলকে কালো দেখাবে। কারণ জবা ফুল লাল ব্যতীত সব আলো শোষণ করে। ঘরের নীল আলো জবা ফুলের ওপর পড়লে জবা ফুল তা শোষণ করে নেবে, কোনো আলোই প্রতিফলিত করবে না।

কোনো বস্তুর রং সাদা বা কালো বলতে কী বোঝ?

কালো বা সাদা কোনো মৌলিক বর্ণ নয়। কোনো বস্তু যদি সব আলো শোষণ করে নেয় তবে তাকে কালো দেখায় এবং যদি সূর্যালোকের সাতটি বর্ণের আলোই প্রতিফলিত করে তবে তাকে সাদা দেখায়। যেমন – কালো ছাতার ওপর সূর্যালোক পড়লে ছাতা সব আলো শোষণ করে নেয় কোনো আলোই প্রতিফলিত করে না তাই কালো ছাতা কালো দেখায়, আবার সাদা কাপড়ে সূর্যের আলো পড়লে কাপড় সব বর্ণের আলোকেই প্রতিফলিত করে তাই সাদা কাপড়কে সাদা দেখায়।

নীল কাচের ভিতর দিয়ে সাদা ফুলকে কেমন দেখাবে?

নীল কাচের ভিতর দিয়ে সাদা ফুলকে নীল দেখাবে। সাদা ফুল থেকে আগত সাতটি বর্ণের আলো নীল কাচে প্রবেশ করলে নীল কাচ নীল রং ব্যতীত সব আলো শোষণ করে নেবে এবং দর্শকের চোখে শুধুমাত্র নীল আলোই আসবে। তাই ফুলকে নীল দেখাবে।

স্বাভাবিক বিচ্ছুরণ কাকে বলে?

কোনো মাধ্যমে কোনো যৌগিক আলোকরশ্মির বিচ্ছুরণ যদি এমন হয় যে তরঙ্গদৈর্ঘ্য বৃদ্ধির সঙ্গে চ্যুতি হ্রাস পায় তাহলে তাকে স্বাভাবিক বিচ্ছুরণ বলে।

একটি লাল কাচের মধ্য দিয়ে সূর্যকে দেখলে কেমন দেখাবে?

লাল কাচের ওপর সূর্যের আলো পড়লে, লাল কাচ লাল ব্যতীত সব আলোকে শোষণ করে নেয় এবং দর্শকের চোখে শুধুমাত্র লাল আলোই আসে। তাই সূর্যকে লাল দেখাবে।

একটি লাল ও নীল কাচকে একসঙ্গে রেখে সামনে থেকে দেখলে কেমন দেখাবে?

লাল কাচের ওপর সূর্যের আলো পড়লে, লাল কাচ লাল ব্যতীত সব আলোকে শোষণ করে নেয় তাই নীল কাচের ওপর শুধুমাত্র লাল আলো আপতিত হয়। কিন্তু নীল কাচ আবার লাল আলোকে শোষণ করে নেয়, ফলে দর্শকের চোখে কোনো আলোই পৌঁছোবে না।

পরিপূরক বর্ণ কাকে বলে?

সাদা আলোর বর্ণালির একদিকের কোনো বর্ণের সঙ্গে বিপরীত দিকের কোনো বর্ণ সঠিক অনুপাতে মিশিয়ে যদি সাদা বর্ণ পাওয়া যায় তাহলে ওই দুটি বর্ণকে পরিপূরক বর্ণ বলা হয়। যেমন – নীল ও হলুদ হল পরিপুরক বর্ণ বা গাঢ় নীল ও লাল হল পরিপূরক বর্ণ।

সাদা জামাকাপড় কাচার পর নীল দেওয়া হয় কেন?

কয়েকবার কাচার পর সাদা জামাকাপড় কিছুটা হলদে দেখায়। তখন উপযুক্ত পরিমাণ নীল, জলে গুলে তাতে ওই জামাকাপড় ডোবালে হলদে ভাব কমে যায় এবং জামাকাপড় ধবধবে সাদা লাগে। এর কারণ নীল ও হলুদ পরস্পর পরিপূরক বর্ণ।

আলো কী ধরনের তরঙ্গ? আলোকতরঙ্গের বেগের রাশিমালাটি লেখো।

আলো হল তড়িৎচুম্বকীয় তরঙ্গ।

আলোকতরঙ্গের তরঙ্গদৈর্ঘ্য \( \lambda \), কম্পাঙ্ক \( \nu \) হলে শূন্যস্থানে আলোর বেগ, \( c=\nu\lambda \)।

অদৃশ্য আলো (invisible ray) বলতে কী বোঝ?

বায়ুতে যে সমস্ত আলোর তরঙ্গদৈর্ঘ্য 4000Å থেকে 8000Å -এর মধ্যে সেইসব আলো আমাদের চোখে দর্শনের অনুভূতি সৃষ্টি করে। 4000Å বা বেগুনি বর্ণের আলোর চেয়ে কম তরঙ্গদৈর্ঘ্যের ও 8000Å বা লাল বর্ণের আলোর চেয়ে বেশি তরঙ্গদৈর্ঘ্যের তড়িৎচুম্বকীয় তরঙ্গ আমাদের চোখে দর্শনের অনুভূতি জাগায় না, এদের অদৃশ্য আলো বলা হয়।

তরঙ্গদৈর্ঘ্যের ঊর্ধ্বক্রমানুসারে তড়িৎচুম্বকীয় তরঙ্গের অংশগুলি লেখো।

• \( \gamma \)-রশ্মি [তরঙ্গদৈর্ঘ্যের পাল্লা – \( 10^{-4} \) Å থেকে 0.1Å]
• X-রশ্মি [তরঙ্গদৈর্ঘ্যের পাল্লা – 0.1Å থেকে 100Å]
• অতিবেগুনি রশ্মি [তরঙ্গদৈর্ঘ্যের পাল্লা – 100Å থেকে 4000Å – এর কম]
• দৃশ্যমান আলো [তরঙ্গদৈর্ঘ্যের পাল্লা – 4000Å থেকে 8000Å]
• অবলোহিত তরঙ্গ [তরঙ্গদৈর্ঘ্যের পাল্লা – 8000Å -এর বেশি থেকে 10⁷Å]
• মাইক্রোতরঙ্গ [তরঙ্গদৈর্ঘ্যের পাল্লা – 1 mm থেকে 10 m]
• রেডিয়ো তরঙ্গ [তরঙ্গদৈর্ঘ্যের পাল্লা – 10 m -এর বেশি] তবে তরঙ্গদৈর্ঘ্যের এই পাল্লা পরিবর্তনশীল।

মাইক্রোতরঙ্গ কী জন্য ব্যবহার করা হয়?

বিমান, রকেট প্রভৃতির অবস্থান জানার জন্য রাডার যন্ত্রে মাইক্রোতরঙ্গ ব্যবহার করা হয়। এই তরঙ্গ বহুদূর পর্যন্ত সোজাভাবে যেতে পারে।

X-রশ্মি ও \( \gamma \)-রশ্মির মধ্যে কোনটির শক্তি বেশি ও কেন?

তড়িৎচুম্বকীয় তরঙ্গের শক্তি তরঙ্গদৈর্ঘ্যের ব্যস্তানুপাতিক। X-রশ্মি অপেক্ষা \( \gamma \)-রশ্মির তরঙ্গদৈর্ঘ্য কম তাই X-রশ্মি চেয়ে \( \gamma \)-রশ্মির শক্তি বেশি।

অতিবেগুনি রশ্মির ব্যবহার ও ক্ষতিকারক প্রভাব লেখো।

অতিবেগুনি রশ্মির ব্যবহার –

• জীবাণুনাশক কাজে,
• রত্ন, ঘি প্রভৃতির বিশুদ্ধতা নির্ণয়ে,
• ভিটামিন D উৎপাদনে,
• ত্বকের কিছু সংক্রমণ যেমন সোরিয়াসিস চিকিৎসায়।

ক্ষতিকারক প্রভাব – বেশি পরিমাণ অতিবেগুনি রশ্মি আপতিত হলে অম্লত্ব বা ত্বকের ক্যানসার হতে পারে।

X-রশ্মির ব্যবহার ও ক্ষতিকারক প্রভাব লেখো।

X-রশ্মির ব্যবহার –

• হাড় ভেঙে গেলে বা দাঁতের ভিতরের গঠন জানার জন্য
• বিভিন্ন রোগের কারণ অনুসন্ধান ও ক্যানসারের চিকিৎসায়
• কেলাসিত পদার্থের গঠন জানার জন্য
• গোয়েন্দা দফতরে কোনো নিখোঁজ জিনিসের অনুসন্ধানে।

ক্ষতিকারক প্রভাব – জীবিত কোশের ওপর আপতিত হলে কোশ ক্ষতিগ্রস্ত হয়।

\( \gamma \)-রশ্মির ব্যবহার ও ক্ষতিকারক প্রভাব লেখো।

\( \gamma \)-রশ্মির ব্যবহার –

• রেডিয়ো থেরাপিতে ক্যানসার কোশ ধ্বংস করার কাজে
• শিল্পক্ষেত্রে ঢালাই -এর কোথাও ফাঁক বা বাদ আছে কি না তা পরীক্ষার কাজে।

ক্ষতিকারক প্রভাব – এই রশ্মি জীবিত কোশকে ভীষণভাবে ক্ষতিগ্রস্ত করে।

X-রশ্মি ও \( \gamma \)-রশ্মির মধ্যে দুটি পার্থক্য লেখো।

X-রশ্মি ও \( \gamma \)-রশ্মির মধ্যে পার্থক্য –

X-রশ্মি	\( \gamma \)-রশ্মি
1. তীব্র গতিবেগসম্পন্ন ইলেকট্রন উচ্চ গলনাঙ্কবিশিষ্ট ধাতুকে আঘাত করলে X-রশ্মি উৎপন্ন হয়।	1. তেজস্ক্রিয় মৌলের দুহিতা পরমাণু থেকে \( \gamma \)-রশ্মি নির্গত হয়।
2. X-রশ্মির শক্তি \( \gamma \)-রশ্মির তুলনায় কম।	2. \( \gamma \)-রশ্মির শক্তি X-রশ্মির তুলনায় বেশি।

আলোর বিক্ষেপণ বলতে কী বোঝ?

আলোর তরঙ্গদৈর্ঘ্যের তুলনায় ছোটো কোনো ধূলিকণা বা গ্যাস অণুর ওপর আলোকরশ্মি আপতিত হলে ওই কণা আলোকতরঙ্গ থেকে শক্তি শোষণ করে এবং ওই শক্তিকে একই তরঙ্গদৈর্ঘ্যের তরঙ্গে চারিদিকে ছড়িয়ে দেয়। এই ঘটনাকে আলোর বিক্ষেপণ বলা হয়। সব তরঙ্গদৈর্ঘ্যের আলোর জন্য বিক্ষেপণ সমান হয় না। বেশি তরঙ্গদৈর্ঘ্যের আলোর বিক্ষেপণ কম ও কম তরঙ্গদৈর্ঘ্যের আলোর বিক্ষেপণ বেশি হয়। বৈজ্ঞানিক লর্ড র‍্যালে প্রমাণ করেন যে, বিক্ষেপিত আলোর তীব্রতা \( \left(I\right) \), তার তরঙ্গদৈর্ঘ্যের \( \left(\lambda\right) \)চতুর্থ ঘাতের ব্যস্তানুপাতিক অর্থাৎ \( I\propto\frac l{\lambda^4} \)

দিনের বেলায় আকাশ নীল দেখায় কেন?

সূর্যের আলো ভূপৃষ্ঠে আসার পূর্বে অনেকটা পথ বায়ুমণ্ডলের মধ্য দিয়ে যায়। বায়ুমণ্ডলের মধ্যে থাকা ক্ষুদ্র ধূলিকণা, গ্যাসের অণু সূর্যালোকের বিক্ষেপণ ঘটায়। দৃশ্যমান আলোর মধ্যে লাল আলোর তরঙ্গদৈর্ঘ্য সবচেয়ে বেশি বলে লাল আলোর বিক্ষেপণ কম হয় কিন্তু নীল বা বেগুনি বর্ণের আলোর তরঙ্গদৈর্ঘ্য কম হওয়ায় এই আলোর বেশি বিক্ষেপণ হয় এবং চারিদিকে ছড়িয়ে পড়ে। আমাদের চোখ বেগুনি অপেক্ষা নীল আলোর জন্য বেশি সংবেদনশীল বলে আমরা আকাশকে নীল দেখি।

চাঁদের আকাশের রং কেমন?

চাঁদে কোনো বায়ুমণ্ডল নেই, তাই চাঁদে সূর্যালোকের বিক্ষেপণ হয় না। চাঁদের আকাশ থেকে কোনো আলোই চন্দ্রপৃষ্ঠে আসে না বলে চাঁদের আকাশ কালো দেখায়।

বিপদ সংকেত হিসেবে লাল আলো ব্যবহৃত হয় কেন?

দৃশ্যমান আলোগুলোর মধ্যে লাল আলোর তরঙ্গদৈর্ঘ্য সবচেয়ে বেশি, ফলে লাল আলোর বিক্ষেপণ সবচেয়ে কম হয়। তাই দৃষ্টি আকর্ষণ করার জন্য বিপদ সংকেত হিসেবে লাল আলো ব্যবহার করা হয়।

সূর্যোদয় বা সূর্যাস্তের সময় সূর্যকে লাল দেখায় কেন?

সূর্যোদয় বা সূর্যাস্তের সময় সূর্য দিগন্তে থাকে, তাই সূর্যরশ্মিকে বায়ুমণ্ডলের মধ্য দিয়ে অনেকটা বেশি পথ অতিক্রম করতে হয়। সূর্যালোকের সাতটি আলোর মধ্যে লাল আলোর তরঙ্গদৈর্ঘ্য সবচেয়ে বেশি বলে বিক্ষেপণ কম হয়। অন্যান্য কম তরঙ্গদৈর্ঘ্যের আলোগুলির বিক্ষেপণ বেশি হয় বলে চারিদিকে ছড়িয়ে যায়, ভূপৃষ্ঠে এসে পৌঁছোয় না। শুধুমাত্র লাল বর্ণের আলো ভূপৃষ্ঠে আসতে পারে তাই সূর্যোদয় বা সূর্যাস্তের সময় সূর্যকে লাল দেখায়।

গাড়ির কুয়াশাভেদী আলো হলুদ হয় কেন?

কুয়াশা দৃশ্যমান আলোকে চারিদিকে বিক্ষিপ্ত করে দেয়, তাই দূরের জিনিস দেখা যায় না। হলুদ বর্ণের আলোর তরঙ্গদৈর্ঘ্য তুলনামূলকভাবে বেশি হওয়ায় বিক্ষেপণ কম হয় এবং কুয়াশার মধ্য দিয়ে দেখতে সুবিধা হয়। তবে লাল আলোর বিক্ষেপণ আরও কম কিন্তু চোখ লাল অপেক্ষা হলুদ আলোতে বেশি সংবেদনশীল তাই গাড়ির কুয়াশাভেদী আলো (fog light) হলুদ বর্ণের হয়।

---

আমরা আমাদের আর্টিকেলে দশম শ্রেণীর ভৌতবিজ্ঞানের পঞ্চম অধ্যায় ‘আলো’ এর কিছু সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর নিয়ে আলোচনা করেছি। এই প্রশ্নগুলো দশম শ্রেণীর ভৌতবিজ্ঞান পরীক্ষার জন্য বা চাকরির পরীক্ষার জন্য অনেক গুরুত্বপূর্ণ। কারণ এই প্রশ্নগুলি দশম শ্রেণীর পরীক্ষা বা চাকরির পরীক্ষায় প্রায় দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা হলে, আপনারা আমার সাথে টেলিগ্রামে যোগাযোগ করতে পারেন, আমরা উত্তর দেওয়ার চেষ্টা করবো। তাছাড়া নিচে আমাদের এই পোস্টটি আপনার প্রিয়জনের সাথে শেয়ার করুন, যাদের এটি প্রয়োজন হতে পারে। ধন্যবাদ।